A Matemática da Força de Coriolis

Disciplina de Matemática Aplicada - UFRGS- Profª Irene Strauch
A Matemática da Força de Coriolis:
Quando se deseja fazer medições em sistemas que estão girando, como a Terra, é
necessário examinar cuidadosamente os efeitos que aparecem. Diferentemente do
movimento de translação que é relativo, o movimento de rotação é uma propriedade
absoluta. Ou seja, pode-se determinar se um corpo está ou não em rotação, sem relacioná-lo
à posição de qualquer outro objeto, porque há forças associadas apenas ao movimento de
rotação. Uma destas forças é a já conhecida força centrífuga e a outra é a força de Coriolis,
a qual desempenha uma importante função na circulação da atmosfera e dos oceanos.
Com o objetivo de deduzir o aparecimento destas forças, vamos determinar inicialmente, os
vetores velocidade e aceleração para um referencial em rotação (não-inercial), quando
observados de um referencial fixo (inercial).
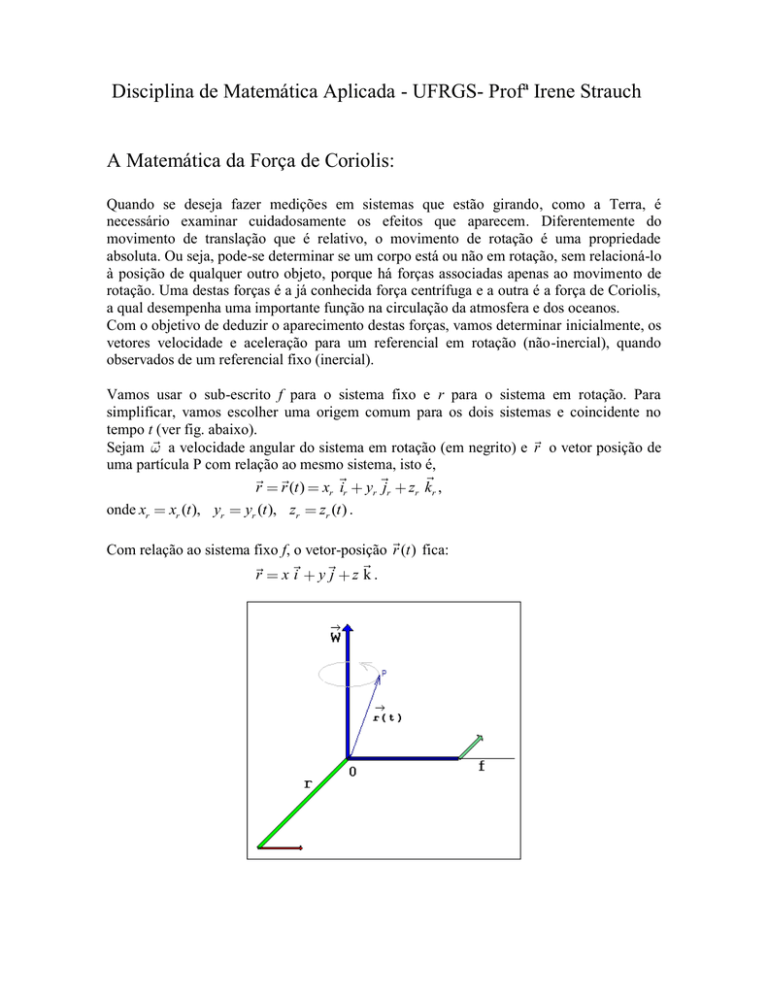
Vamos usar o sub-escrito f para o sistema fixo e r para o sistema em rotação. Para
simplificar, vamos escolher uma origem comum para os dois sistemas e coincidente no
tempo t (ver fig. abaixo).
Sejam
a velocidade angular do sistema em rotação (em negrito) e r o vetor posição de
uma partícula P com relação ao mesmo sistema, isto é,
r r (t ) xr ir yr jr zr kr ,
onde xr xr (t ), yr yr (t ), zr zr (t ) .
Com relação ao sistema fixo f, o vetor-posição r (t ) fica:
r
xi
yj
z k.
A diferença entre essas duas descrições é que os vetores unitários (ir , jr , kr ) do referencial
em rotação possuem direção e sentido que variam com o tempo, enquanto que os vetores
unitários (i , j , k ) do referencial fixo são constantes em direção e sentido.
Assim, o vetor velocidade da partícula P, medido no referencial fixo é:
dr
dt
vf
dx
i
dt
dy
j
dt
dz
k
dt
Ou, tomando o mesmo raio-vetor referenciado ao sistema em rotação, podemos escrever:
dr
d
vf
xr ir yr jr zr kr
dt dt
dxr
ir
dt
vr
xr
dyr
jr
dt
dir
dt
yr
dzr
kr
dt
djr
dt
zr
xr
dir
dt
yr
dkr
dt
djr
dt
zr
,
dkr
dt
(eq.( I ))
Onde vr é a velocidade da partícula P relativa ao sistema em rotação. Os termos restantes
expressam o movimento do sistema em rotação com relação ao sistema fixo.
Por outro lado, sabemos do estudo do movimento de rotação que, quando uma partícula P
gira com velocidade angular w em torno de um eixo fixo, conforme figura abaixo,
dr
r.
o vetor velocidade linear v é dado por: v
dt
Adaptando este resultado aos três termos restantes, temos
dir
dt
ir
djr
dt
,
jr ,
dkr
dt
kr
,
onde o 1º representa o vetor velocidade linear no ponto (1, 0,0), no sistema em rotação em
qualquer tempo t . E de maneira análoga, o 2º representa a velocidade no ponto (0, 1,0) e o
3º a velocidade no ponto (0, 0,1). Usando estes resultados na eq, (I), podemos escrever:
vf
vr
xr ir
yr jr
zr k r
vr
r
(eq.(II )) .
Isto é, o vetor velocidade medido no sistema fixo é igual ao vetor velocidade medido no
sistema em rotação mais o vetor velocidade do sistema em rotação relativo ao sistema fixo.
Esta afirmação ainda pode ainda ser escrita matematicamente, na forma operacional como:
d
dt
r
f
d
dt
r .
r
Esta fórmula é válida para qualquer vetor e não apenas para o vetor posição r . Assim, em
casos mais gerais, a leitura desta fórmula é: “a taxa de variação de um certo vetor no
referencial fixo(f) é igual à taxa de variação do mesmo vetor no referencial em rotação (r)
mais o produto vetorial entre a velocidade angular do referencial em rotação e o referido
vetor”.
Se este vetor arbitrário for a velocidade linear v f com relação ao referencial fixo, teremos:
d
dt
d
dt
vf
f
vf .
r
O termo da esquerda é a definição do vetor aceleração a f no sistema fixo. À direita,
façamos a substituição de v f pelo resultado obtido na eq.(II). Assim,
d
dt
af
dvr
dt
vr
r
r
d
dt
r
vr
r
(eq.III )
Esta expressão relaciona a aceleração a f com as acelerações medidas no sistema em
rotação. Observe que se
0 então a f
dvr
.
dt
Vamos agora, identificar estas acelerações que aparecem no sistema em rotação (eq.III):
dv
-O termo r é a aceleração medida no sistema em rotação, ar .
dt
d
r , encontramos:
-Usando a derivada de um produto para o termo
dt
d
d
dr
r
r
.
dt
dt
dt
Se supusermos que a velocidade angular
d
r
dt
é constante, então o 2º termo se reduz a
dr
vr .
dt
-Com isso, o 2º e o 3º termos se somam, dando 2 vr .
Este é o termo que dá origem aceleração de Coriolis.
-O 4º termo,
(
r ) é um vetor normal a
De acordo com a figura ao lado,
vetores
e r.
.
é o ângulo entre os
Usando a regra do produto vetorial, o módulo deste
triplo produto vetorial é 2 r sen .
Este termo é identificado como a aceleração centrípeta
e a força correspondente é a força centrípeta.
Portanto, um observador inercial descreveria o movimento de rotação de um corpo de
massa m, como uma força resultante F f dada pela 2ª Lei de Newton da Mecânica como a
soma das seguintes forças:
Ff
Fr
2m(
vr )
Fcentrípeta
Já para o observador no sistema em rotação, tudo se passa como se a partícula se movesse
sob a ação de uma força efetiva dada por:
Fr
Ff
2m(
vr )
Fcentrípeta .
Como este observador não-inercial também conhece a 2ª Lei de Newton, identificará no 1º
termo a força resultante. O 2º e o 3 º termos são forças que só existem porque o sistema gira
vr ) é a chamada força de Coriolis e o 3º
com velocidade angular . O 2º termo 2m(
termo Fcentrípeta é a força conhecida como força centrífuga, com sentido oposto à força
centrípeta.
Qualquer um que tenha tentado caminhar em uma plataforma girante, deve ter sentido os
efeitos da força de Coriolis. Ela deflete o movimento em uma direção perpendicular ao
plano determinado por e vr (ver fig. abaixo).
Uma interessante constatação da existência desta força ficou conhecida como o pêndulo de
Foucault. Um pêndulo longo em oscilação acabará por precessionar devido à força de
Coriolis. Este movimento é uma evidência visível do movimento de rotação da Terra,
independente de qualquer observação astronômica.
Quem foram Coriolis e Foucault ?
Gaspard-Gustave Coriolis foi um engenheiro francês que, em 1835, publicou um trabalho
científico, resultado de suas pesquisas envolvendo máquinas em rotação, como as rodas
d’água, no qual menciona a existência de uma força do tipo força centrífuga e deduz com
bastante precisão sua fórmula matemática.
No início do século XX, o termo força de Coriolis começa a ser usado em meteorologia.
Os efeitos da força de Coriolis são hoje bem conhecidos no movimento dos ventos em
centros de baixa pressão. Isto é, quando uma área de baixa pressão se forma na atmosfera, o
ar tende a fluir em sua direção movido pelos gradientes de pressão, mas será defletido
perpendicularmente à sua velocidade pela força de Coriolis. Um sistema de equilíbrio pode
então se estabelecer, criando um movimento circular e dando origem a uma formação tipo
campo de spin, característica dos fluxos ciclônicos.
Também em escala microscópica os efeitos da força de Coriolis estão presentes e podem
ser observados. Por exemplo, em moléculas poliatômicas, o movimento da molécula pode
ser descrito como o movimento de rotação de um corpo rígido, superposto ao movimento
de vibração interna dos átomos, entorno de sua posição de equilíbrio. Os espectros destas
moléculas apresentam, conseqüentemente, uma mistura de modos rotacionais e
vibracionais.
Jean Bernard Leon Foucault foi um físico e astrônomo francês que, em 1851, realizou a 1ª
demonstração experimental do movimento de rotação da Terra . O aparato experimental
consistiu de um longo pêndulo, deixado livre para oscilar em qualquer plano vertical. A
apresentação mais sensacional foi a realizada no Panthéon de Paris, onde usou uma massa
de 28 kg suspensa em um fio de 67m de comprimento. O movimento do pêndulo em um
sistema inercial seria um movimento harmônico simples, mas devido ao movimento de
rotação da Terra estabelece-se, gradualmente, um movimento de precessão, resultante da
composição da força gravitacional e da força de Coriolis que aderem do movimento de
rotação da Terra.
Para uma descrição qualitativa das forças no movimento de rotação, sugerimos a leitura do
parágrafo 19-4 do Feymann, Lições de Física, Vol. I.
Animações interessantes podem ser acessadas no endereço do Wikipedia, usando como
palavras-chaves: Coriolis e Foucault ou no Amazing Physics do youtube.
Sobre o movimento da água em ralos de pia, sugerimos o interessante artigo dos
professores Fernando Lang da Silveira e Rolando Axt, publicado no Caderno Catarinense
de Física, Florianópolis, v.17, n.1: p.22-26, 2000.