Escoamento completamente desenvolvido

Mecânica dos Fluidos - Professor Eduardo Loureiro
Escoamento completamente desenvolvido
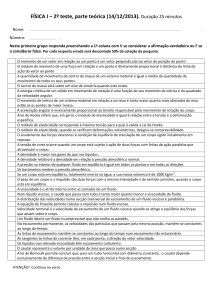
A figura mostra um escoamento laminar na região de entrada de um tubo circular. Uma camada limite desenvolve-se
ao longo das paredes do duto. A superfície do tubo exerce um força de cisalhamento retardante sobre o
escoamento; assim a velocidade do fluido nas proximidades da parede é reduzida. O efeito da superfície sólida é
sentido cada vez mais para dentro do escoamento. Suficientemente longe da entrada do tubo a camada limite em
desenvolvimento atinge a linha de centro do mesmo e o escoamento torna-se inteiramente viscoso. Quando isto
acontece e a forma do perfil de velocidades não se altera com o avanço do escoamento diz-se que o mesmo
encontra-se completamente desenvolvido. A distância a jusante, a partir da entrada, até o local em que o
escoamento torna-se completamente desenvolvido é chamada de comprimento de entrada.
Para o escoamento laminar, o comprimento de entrada é uma função do número de Reynolds:
L
VD
 0,06
D

Como no escoamento laminar admite-se número de Reynolds de até 2300, o comprimento de entrada pode atingir
distâncias tão grandes como:
L  0,06 Re D  0,062300D  138D
Se o escoamento for turbulento, a mistura intensa entre camadas do fluido causa o crescimento mais rápido da
camada limite e experiências mostram que o comprimento de entrada se reduz para distâncias entre 25 e 40
diâmetros do tubo.
Mecânica dos Fluidos - Professor Eduardo Loureiro
Lei de Poiseuille
Quando a velocidade de um fluido, em qualquer ponto, é constante no tempo, o escoamento é dito estacionário ou
permanente. Então, cada partícula que passa por um determinado ponto o faz sempre com a mesma velocidade. Em
um outro ponto, as partículas podem passar com outra velocidade, mas aí, também, a velocidade é sempre a mesma.
Consideremos, agora, o escoamento de um fluido viscoso através de um tubo cilíndrico, com uma velocidade não
muito grande, de modo que o escoamento é laminar e estacionário. A camada mais externa adere à parede e tem
velocidade nula. A parede exerce sobre esta camada uma força de sentido contrário ao movimento do fluido e ela,
por sua vez, exerce uma força de mesmo sentido sobre a camada seguinte, e assim por diante. A camada central tem
a velocidade máxima. O escoamento do fluido é como o movimento de vários tubos encaixados, cada qual
deslizando com velocidade maior que o vizinho externo.
Consideremos um elemento cilíndrico de fluido, de raio r e
comprimento L, coaxial com o tubo, que se escoa por efeito de uma
diferença de pressão. A força que impulsiona o fluido tem módulo
F  F1  F2  Pr 2 . Esta força deve estar em equilíbrio com a força de
viscosidade que atua na superfície do elemento cilíndrico considerado,
com área A  2rL , de modo que:

F
dv

A
dy
Pr 2   (2rL)
dv
dr
dv  (P / 2L)rdr
Integrando esta expressão desde um r genérico, para o qual a correspondente camada de fluido tem uma velocidade
v, até r = R, para o qual a correspondente camada de fluido tem v = 0, obtemos:
v(r ) 

1
(P / L) R 2  r 2
4

Mecânica dos Fluidos - Professor Eduardo Loureiro
Lei de Poiseuille
v(r ) 

1
(P / L) R 2  r 2
4

Assim, a velocidade de uma dada camada cilíndrica do fluido é diretamente proporcional ao gradiente de pressão e
inversamente proporcional ao coeficiente de viscosidade. Ainda, a velocidade das partículas do fluido é máxima em
r = 0 (no centro do tubo), diminuindo até zero em r = R (junto às paredes).
Considerando agora uma camada cilíndrica de fluido, com raio interno r e raio externo r + dr, que se move com
velocidade de módulo v. No intervalo de tempo dt, o volume de fluido que atravessa uma seção reta do tubo
é dV  (vdt )(dA) , onde . Portanto, levando em conta a expressão acima, temos:
dV 
1
(P / L)( R 2  r 2 )(2 rdr) dt
4
O volume de fluido que escoa através de toda seção reta do tubo de
raio R durante o intervalo de tempo dt é obtido pela integração em r,
desde r = 0 até r = R :
R 2 2


 R4
dV 
(P / L)   R  r rdr  dt 
P dt
2
8

L
0

A vazão, ou seja, o volume de fluido que passa através de uma seção reta do tubo por unidade de tempo,
Q  dV dt é dada por:
R 4 P PD 4
Q

8 L
128L
Esta equação é conhecida como a equação de Poiseuille.
Mecânica dos Fluidos - Professor Eduardo Loureiro
Carga total, de pressão de velocidade e potencial
Ao observar o que acontece com o exemplo de um reservatório que abastece um duto, podemos
verificar a relação entre estas cargas.
p1 v12
p
v2

 z1  H  2  2  z2
g 2 g
g 2 g
Para analisar o escoamento no tubo nós aplicamos a equação de Bernoulli ao longo de uma linha de
corrente do ponto 1 na superfície do reservatório até o ponto 2 na saída do tubo. E nós sabemos
que a energia total por unidade de peso ou a carga total não varia - ela é constante - ao longo de uma
linha de corrente. Mas, qual o valor desta constante?
Nós podemos calcular a carga total H (ou altura total, já que H é a soma de parcelas que podem ser
expressas em unidades de altura de uma coluna de liquido).
No reservatório, p1 = 0 pois p1 é a pressão atmosférica e a pressão manométrica atmosférica é
zero. Se o reservatório for muito grande a velocidade no ponto 1 pode ser considerada desprezível
se comparada com a velocidade no tubo. Portanto v1 = 0, então, no reservatório, a altura total = H
= z1 que é a elevação do reservatório.
Mecânica dos Fluidos - Professor Eduardo Loureiro
Carga total, de pressão de velocidade e potencial
No gráfico abaixo a linha de altura total é mostrada. Se nós conectarmos piezômetros (tubos verticais
abertos, preenchidos com o mesmo líquido cuja pressão desejamos medir) em diferentes pontos ao longo
do tubo, quais os níveis mostrados quando o tubo estiver fechado na extremidade?
Como podemos ver, com velocidade zero, os piezômetros apresentam um mesmo nível que corresponde a
linha de altura (ou carga) total.
Em cada ponto da linha, quando v = 0.
p
zH
g
a altura de cada piezômetro corresponde à carga (ou altura) de pressão e seu valor é dado por
p
.
g
Mecânica dos Fluidos - Professor Eduardo Loureiro
Carga total, de pressão de velocidade e potencial
O que aconteceria com as alturas mostradas nos piezômetros se o fluido apresentar uma
velocidade v  0?
Nós já sabemos que quando a velocidade aumenta a pressão diminui.
Na figura acima, os níveis foram reduzidos por uma quantidade igual à carga de velocidade,
v2
.
2g
Como o tubo tem diâmetro constante, nós podemos ver que a altura de velocidade é constante e
está representada pela segunda linha tracejada horizontal.
Mecânica dos Fluidos - Professor Eduardo Loureiro
Carga total, de pressão de velocidade e potencial
O que aconteceria se o tubo não fosse de diâmetro constante? Vejamos na figura abaixo onde o
tubo anterior foi substituído por outro com três diâmetros diferentes e com a seção intermediária
de diâmetro maior.
A altura de velocidade em cada ponto é diferente agora. Isto porque a velocidade é diferente em
cada ponto.
Mecânica dos Fluidos - Professor Eduardo Loureiro
Perdas devido ao atrito
Em um tubo real há perdas de energia devido ao atrito, que devem ser levadas em conta quando
forem significantes. Como se comportarão as cargas de pressão e de velocidade com o atrito? Se
considerarmos novamente o tubo com diâmetro constante, nós teremos uma situação como a
mostrada abaixo:
A perda de energia devido ao atrito, cujo símbolo é ht, também pode ser escrita como uma altura
de coluna de líquido.
p1 v12
p2 v22

 z1 

 z2  ht
g 2 g
g 2 g
Mecânica dos Fluidos - Professor Eduardo Loureiro
Perdas de carga em tubulações
Na equação, os termos entre parêntesis representam a energia mecânica por unidade de massa em uma seção. O
termo hT, igual à diferença em energia mecânica por unidade de massa entre as duas seções (1) e (2), representa a
conversão (irreversível) de energia mecânica em energia térmica indesejada e perda de energia através de
transferência de calor. hT é o que chamamos de perda de carga total.
 p1 v12
  p2 v22

   gz1      gz2   ht
2
 2
  

[1]
A perda de energia tem dimensões de energia por unidade de massa [FL/M], equivalente a [L2/t2]. Se dividirmos cada
termo da equação [I] pela aceleração da gravidade, g, as dimensões resultantes de hT serão [(L2/t2)(t2/L)] = [L], ou
altura de uma coluna do líquido em escoamento.
A equação [I] pode ser usada para calcular a diferença de pressão entre quaisquer dois pontos num sistema de
tubos, desde que a perda de carga possa ser determinada.
Contribuindo para a perda de carga total teremos:
A soma das perdas distribuídas, hd, devidas aos efeitos de atrito no escoamento completamente
desenvolvido em tubos de seção constante


A soma das perdas localizadas, hl, devidas a entradas, acessórios, mudanças de área, etc.
Mecânica dos Fluidos - Professor Eduardo Loureiro
Perdas distribuídas
 p1 v12
  p v2

   gz1    2  2  gz2   ht
2
 2
  

Para o escoamento completamente desenvolvido num tubo de área constante, as perdas localizadas
não existem, hl = 0, e a equação do balanço de energia [I] reduz-se a:
p1  p2

 g z2  z1   hd
Se o tubo for horizontal, então z2 = z1 e
p1  p2


p

 hd
[II]
Como a perda de carga representa a energia mecânica convertida em térmica, por efeitos de atrito,
ela depende tão somente dos detalhes do escoamento através do conduto e independe da
orientação do duto. Portanto, a perda de carga distribuída pode ser expressa como a perda de
pressão.
Mecânica dos Fluidos - Professor Eduardo Loureiro
Perdas distribuídas
p1  p2



p

 hd
Para o escoamento laminar a queda de pressão pode ser calculada analiticamente e a perda de
carga distribuída é dada por:
R 4 P PD 4
Q

8 L
128L


128LQ 128LV D 2 4
L V
P 


32
D 4
D 4
D D
Equação de Poiseuille
L V L V 2 
 
 64

hd  32

D D D 2  VD 

2
 64  L V
hd   
 Re  D 2
Para o escoamento turbulento não podemos avaliar a queda de pressão analiticamente; devemos
recorrer a dados experimentais e utilizar a análise dimensional para correlacioná-los.
Mecânica dos Fluidos - Professor Eduardo Loureiro
Perdas distribuídas
A queda de pressão, Δp, devida ao atrito, num tubo horizontal de área constante, depende do diâmetro do tubo, D, do seu
comprimento, L, da sua rugosidade, e, da velocidade média do escoamento, V, da massa específica, ρ, e da viscosidade do
fluido, μ.
p  F D, L, e,V ,  ,  
Da análise dimensional, os resultados formam uma correlação da forma:
p
L e

   Re, , 
2
V
D D

  L e
p
 f 
, , 
2
V
 VD D D 
Da equação [II], verificamos que:
hd
L e

   Re, , 
2
D D
V

Esta é a relação funcional que conseguimos com a análise dimensional. Experiências mostram que a perda de carga é
diretamente proporcional à fração L/D. Portanto,
hd 
L 
e
1  Re, V 2
D 
D
Uma vez que a função é ainda indeterminada dividimos por 2 o segundo membro da equação, gerando uma nova função :
hd 


A função desconhecida,  2  Re,
E, finalmente:
L 
e V
 2  Re, 
D 
D 2
2
e
 , é definida como o fator de atrito, f.
D
L V2
hd  f
D 2
Mecânica dos Fluidos - Professor Eduardo Loureiro
Rugosidade relativa:
A rugosidade relativa pode ser obtida de gráficos ou tabelas:
Tubo
Aço rebitado
Concreto
Madeira
Ferro fundido
Ferro galvanizado
Ferro fundido asfaltado
Aço comercial ou ferro forjado
Tubos trefilados
Rugosidade (mm)
0,9-9
0,3-3
0,2-0,9
0,26
0,15
0,12
0,046
0,0015
Mecânica dos Fluidos - Professor Eduardo Loureiro
O diagrama de Moody:
e
 0,0006
D
Re  4 104
Mecânica dos Fluidos - Professor Eduardo Loureiro
O diâmetro hidráulico:
As correlações para escoamento turbulento em tubos são estendidas para uso com geometrias
não-circulares pela introdução do diâmetro hidráulico, definido como:
Dh 
4A
P
Onde A é a área de seção transversal e P é o perímetro molhado, o comprimento da parede em
contato com o fluido escoando em qualquer seção transversal.
Desta forma, para um duto circular:
A
D 2
4
P  D
 
4  D 2
4A
4
Dh 
  
D
P
D