Análise do Estado de Tensões

a
1 Lista de exercícios
Análise do estado de tensões
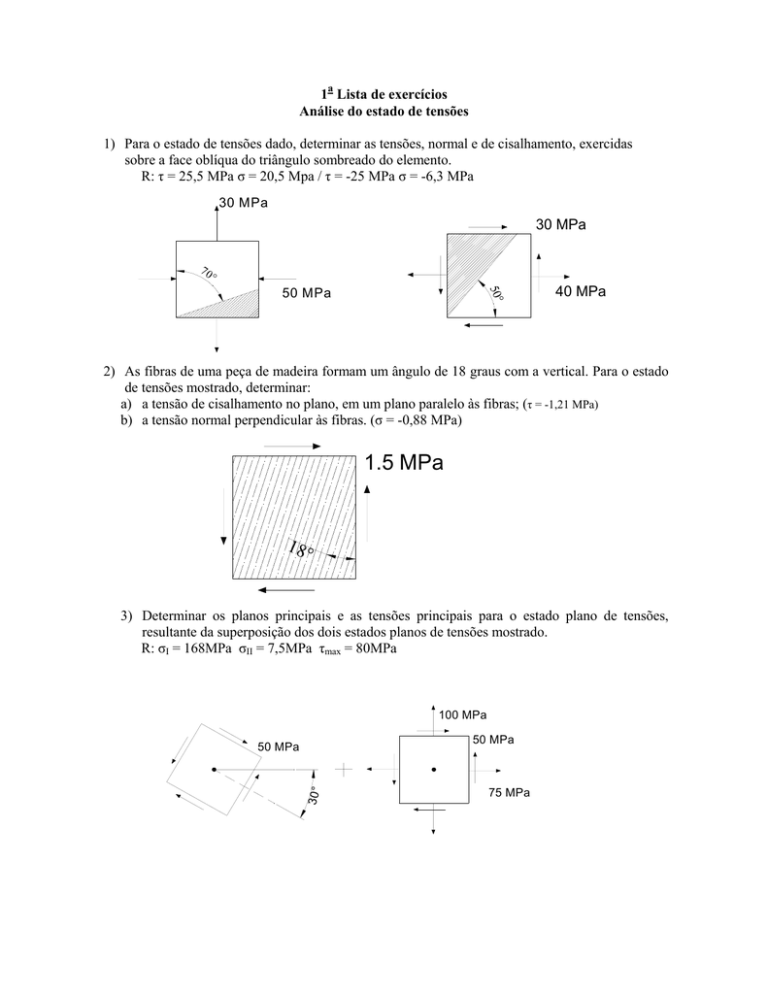
1) Para o estado de tensões dado, determinar as tensões, normal e de cisalhamento, exercidas
sobre a face oblíqua do triângulo sombreado do elemento.
R: τ = 25,5 MPa σ = 20,5 Mpa / τ = -25 MPa σ = -6,3 MPa
30 MPa
30 MPa
70
°
50°
50 MPa
40 MPa
2) As fibras de uma peça de madeira formam um ângulo de 18 graus com a vertical. Para o estado
de tensões mostrado, determinar:
a) a tensão de cisalhamento no plano, em um plano paralelo às fibras; (τ = -1,21 MPa)
b) a tensão normal perpendicular às fibras. (σ = -0,88 MPa)
1.5 MPa
18°
3) Determinar os planos principais e as tensões principais para o estado plano de tensões,
resultante da superposição dos dois estados planos de tensões mostrado.
R: σI = 168MPa σII = 7,5MPa τmax = 80MPa
100 MPa
50 MPa
3 0°
50 MPa
75 MPa
4) Uma força de 19.5 kN é aplicada no ponto D da barra de ferro fundido mostrado. Sabendose que a barra tem um diâmetro de 60 mm, determinar as tensões principais e a máxima
tensão de cisalhamento nos pontos H e K. (R: PONTO H: σI = 73,5 MPa / σII = -9,5 MPa /
τmax = 41,5 MPa - PONTO K: σI = 10 MPa / σII = -140 MPa / τmax = 75 MPa)
B
D
19,5 kN 300 mm
H K
100 mm
E
A
125 mm
150 mm
z
x
5) Uma força vertical de 18 kN é aplicada na extremidade A da barra AB que é, soldada a um
tubo de alumínio extrudado de espessura uniforme de 6 mm. Determinar as tensões
principais e a máxima tensão de cisalhamento no:
a) ponto H (R: σI = 67 MPa; σII = –14 MPa; τmax = 41 MPa)
b) ponto K (R: σI = 17 MPa; σII = –17 MPa; τmax = 17 MPa)
18 kN
100 m m
25 mm
120 m m
A
H
B
K
100 m m
50 mm
50 mm
6) Sabe-se que o tubo da figura tem paredes de espessura constante de 6 mm. Determinar as
tensões principais e de cisalhamento máxima:
a) No ponto H;
b) No ponto K.
60 mm
Resposta:
Ponto H:
σI = 87 MPa
σII = -4 MPa
τmax = 45,5 MPa
Ponto K:
σI = 54 MPa
σII = -54 MPa
τmax = 54 MPa
H
120 mm
K
40 mm
80 mm
160 mm
3 mm
30 kN
7) Para viga com carregamento indicado, calcular as tensões principais e de cisalhamento
máxima, nos três pontos indicados. Usar círculo de Mohr.
z
y
24 mm
60 mm
a
b
c
15 mm
30 mm
180 mm
750 N
40 mm
32 mm
Resposta:
Ponto a:
σI = 18,60 MPa
σII = -0,20 MPa
τmax = 9,40 MPa
Ponto b:
σI = 21,35 MPa
σII = -0,10 MPa
τmax = 10,725 MPa
Ponto c:
σI = 24,12 MPa
σII = 0 MPa
τmax = 12,06 MPa
16 mm
500 N
10 kN
x
8) Três forças são aplicadas a um perfil de aço laminado W250 x 49,1, como mostrado.
Determinar as tensões, principais e de cisalhamento máxima, nos pontos “a” e “c”. Utilizar
círculo de Mohr.
120 mm
y
60 kN
tf
bf
tw
12 kN
30 kN
140 mm
c
d
12 kN
c
a
Perfil W250 x 49,1
Resposta:
Ponto a:
σI = 0
σII = -106,7 MPa
τmax = 53,4 MPa
Ponto c:
σI = 13,5 MPa
σII = -23 MPa
τmax = 18 MPa
400 mm
A = 6260 mm2
d = 247 mm
bf = 202 mm
tf = 11 mm
tw = 7,4 mm
Ix = 70,8 . 106 mm4
Iy = 15,23 . 106 mm4
a
x
9) Sabe-se que o tubo da figura tem paredes de espessura constante de 6 mm. Calcular as
tensões principais e de cisalhamento máxima nos três pontos indicados. Obs.: utilizar círculo
y
de Mohr.
75m m
150m m
3000N
Resposta:
Ponto a:
σI = 0
σII = -106 MPa
τmax = 53 MPa
Ponto b:
σI = 1 MPa
σII = -79,5 MPa
τmax = 40 MPa
Ponto c:
σI = 2,6 MPa
σII = -29 MPa
τmax = 15,7 MPa
3000N
x
7500N
125m m
7500N
500m m
25m m
50m m
75m m
a
b
c
10) Calcular as tensões principais e a de cisalhamento máxima para os pontos “a” e “c” da
estrutura abaixo. (R: PONTO a: σI = 38,36 MPa / σII = 0 / τmax = 19,18 MPa - PONTO c:
σI = 11,5 MPa / σII = -30 MPa / τmax = 20,5 MPa)
8 kN
100 mm
100 kN
y
y
8 kN
tw
25 kN
x
500 mm
d
c
x
tf
a
c
a
Perfil W200 x 41,7
A = 5320 mm2
d = 205 mm
bf = 166 mm
tf = 11,8 mm
tw = 7,2 mm
Ix = 40,8 . 106 mm4
Iy = 9,06 . 106 mm4
bf
11) Duas forças são aplicadas a um tubo AB, como mostrado. Sabendo-se que o tubo tem
diâmetros, interno e externo, iguais a 35 mm e 42 mm, respectivamente, determinar as
tensões principais e de cisalhamento máxima, no:
a) Ponto a;
y
b) Ponto b.
45 mm
A
45 mm
1500 N
1200 N
Resposta:
Ponto a:
σI = 28 MPa
σII = -7,5 MPa
τmax = 18 MPa
Ponto b:
σI = 9 MPa
σII = -31 MPa
τmax = 20 MPa
12)
a)
b)
c)
b
a
75 mm
B
z
20 mm
x
Sabendo-se que o diâmetro da barra de aço ABD é de 30 mm, determinar para o ponto H:
Os planos principais (σ: θ = 11° 40’ 30” horário – τ: θ = 33° 19’ 30” anti-horário)
As tensões principais (σI = 34,8 MPa; σII = -104,6 MPa)
A máxima tensão cisalhante, no ponto H. (τmax = 69,7 MPa)
y
150 mm
25 mm
E
150 mm
A
H
B
2 kN
x
225 mm
z
D
13)
Para o estado de tensões mostrado, determinar a máxima tensão de cisalhamento, quando :
a) σy = 80 MPa (τmax = 63 MPa)
y
b) σy = - 80 MPa (τmax = 50 MPa)
σ
y
30 MPa
z
35 MPa
x
14) Para o estado de tensões mostrado, determinar a máxima tensão de cisalhamento, quando:
y
a) τxy = 42 MPa (τmax = 69 MPa)
b) τxy = 96 MPa (τmax = 104 MPa)
40 MPa
τxy
120 MPa
z
x
15) Determinar, para o estado de tensões indicado, a tensão de cisalhamento máxima quando:
a) σy = 14 MPa (τmax = 68 MPa)
b) σy = 98 MPa (τmax = 76 MPa)
y
σy
55,2 MPa
96,5 MPa
z
x
16) O estado plano de tensões mostrado ocorre em um componente feito de aço com σe = 250
MPa. Usando o critério da máxima tensão de cisalhamento, determinar se o escoamento
ocorre quando:
a) σy = 160 MPa (ocorre o escoamento; τmax = 130 MPa)
σy
b) σy = 40 MPa (não ocorre o escoamento; τmax = 117 MPa)
c) σy = - 40 MPa (ocorre o escoamento; τmax = 141 MPa)
100 MPa
160 MPa
17) Um eixo de 36 mm de diâmetro é feito de uma classe de aço, com uma resistência ao
escoamento na tração de 250 MPa. Usando o critério da máxima tensão de cisalhamento,
determinar a intensidade do torque T, para que o início do escoamento ocorra quando P =
200 kN. (Resposta: T = 708.000 Nmm)
P
T
36 mm
18) O estado plano de tensões indicado é esperado em um alumínio fundido. Sabendo-se que
para a liga de alumínio usada a σut = 80 MPa e σuc = 200 MPa, e usando o critério de Mohr,
determinar se a ruptura irá ocorrer. (Resposta: A ruptura não irá ocorrer; σI = 32 MPa e σII =
-113 MPa).
80 MPa
60 MPa
19) Um elemento de máquina é feito de ferro fundido para o qual σut = 51,7 MPa e σuc = 124,1
MPa. Determinar, para cada um dos estados planos de tensões indicado, e usando o critério
da Mohr, a tensão σo para a qual deve ocorrer a ruptura do elemento.
1/2 σo
σo
(a)
Resposta:
a) σo = 51,7 MPa
b) σo = 42,8 MPa
c) σo = 56,4 MPa.
1/2 σo
1/2 σo
σo
(b)
σo
(c)
20) O estado plano de tensões mostrado ocorre em uma barra feita de um tipo de aço, com
tensão ao escoamento na tração de 300 MPa. Determinar o coeficiente de segurança, em
relação ao escoamento, usando:
a) Critério da máxima tensão de cisalhamento;
150 MPa
b) Critério da máxima energia de distorção.
Resposta:
a) coef.seg. = 1,76
b) coef.seg. = 3,47
50 MPa
40 MPa
21) Para o estado plano de tensões mostrado, determinar:
a) os planos principais (θP = 18° 30’; θC = 26° 30’).
b) as tensões principais (σI = 110 MPa; σII = 10 MPa)
c) a máxima tensão de cisalhamento (τmax = 55 MPa)
100 MPa
30 MPa
20 MPa
22) Uma barra de alumínio fundido é feito de uma liga em que, σut = 80 MPa e σuc = 200 MPa.
Sabendo-se que T dos torques aplicados é gradual e crescente e usando o critério de ruptura
de Mohr, determinar τo para que ocorra a ruptura.
Resposta:
τ0 = 57,1 MPa
T'
τ0
T
23)
Um ponto de um componente de máquina fica submetido ao estado plano de tensões
indicado. O componente é feito de liga de alumínio para o qual σy = 280 MPa. Adotando o
critério de máxima tensão de cisalhamento, determinar o valor da tensão de compressão σy
para o qual o escoamento ocorre.
σy
Resposta: σy = -115,95 MPa.
100 MPa
80 MPa
24)
O tanque de ar comprimido AB tem um diâmetro externo de 250 mm e uma espessura de 8
mm. Nele é montado um colar, no qual uma força P de 40 kN pode ser aplicada em B.
sabendo-se que a pressão interna do tanque é de 5MPa, determinar a máxima tensão de
cisalhamento no:
a) ponto K. (R: τmax = 25,84 MPa).
y
b) ponto L. (R: τmax = 46,44 MPa).
150 mm
B
P
600 mm
L
150 mm
K
A
z
x
25)
O tanque de ar comprimido AB tem um diâmetro externo de 462 mm e uma espessura
uniforme de 6 mm. Sabendo-se que a pressão dentro do vaso é de 130 kPa, determinar as
tensões principais e de cisalhamento máxima, no:
a) Ponto K;
b) Ponto L.
750 mm
K
B
L
Resposta:
Ponto K:
σI = 7,17 MPa
σII = 4,23 MPa
τmax = 1,47 MPa
Ponto L:
σI = 5,55 MPa
σII = 1,95 MPa
τmax = 1,80 MPa
5 kN
500 mm
O vaso de pressão cilíndrico mostrado é fabricado com chapa de aço de 6,35 mm de
espessura, soldada ao longo de uma hélice, formando um ângulo de 30 graus com a
horizontal. Sabendo-se que a tensão normal admissível perpendicular à solda é de 80 MPa,
determinar a maior pressão que pode ser usada no vaso. (R: PMÁX = 400 kPa)
635 mm
2000 mm
26)
A
30