∑ = 0 ∑ = 0 ∑ = 0 ∑ ∑ ∑ ∑

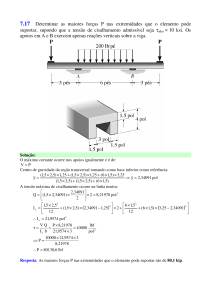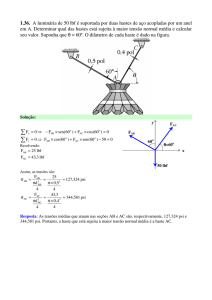
6.2 O eixo está submetido às cargas provocadas pelas correias que passam sobre as
duas polias. Desenhar os diagramas de força cortante e momento. Os mancais em A e
B exercem apenas reações verticais sobre o eixo.
Solução:
400 lbf
300 lbf
x
C
A
B
18 pol
24 pol
VA
D
12 pol
VB
Utilizando as equações de equilíbrio, calculam-se as reações de apoio.
Fx = 0 Não será utilizada pois o enunciado afirma que os apoios exercem apenas reações verticais.
•
∑
Em seguida pode-se resolver a equação:
•
∑M
z
= 0 , assim, tomando um eixo z que passa pelo
ponto B temos:
∑M
•
∑F
y
z
= 0 ⇒ VA × 24 − 400 × 42 + 300 × 12 = 0 ⇒ VA = 550 lbf
usando a equação:
∑F
y
= 0 , temos:
= 0 ⇒ VA + VB − 400 − 300 = 0 ⇒ VB = 150 lbf
Equações de esforços para cada um dos trechos. (Os esforços normais são iguais a zero ,Nx=0)
0 ≤ x ≤ 18 pol
400 lbf
x
Vx
∑F
y
Mx
C
∴ Vx = −400
Nx
∑M
Trecho CA
z
= 0 ⇒ 400x + M x = 0
∴ M x = −400x
400 lbf
18 ≤ x ≤ 42 pol
x
C
= 0 ⇒ −400 − Vx = 0
∑F
Vx
y
Mx
A
550 lbf
Nx
Trecho AB
= 0 ⇒ −400 − Vx + 550 = 0
∴ Vx = 150
∑M
z
= 0 ⇒ 400x − 550( x − 18) + M x = 0
∴ M x = 150x − 9900
42 ≤ x ≤ 54 pol
400 lbf
x
∑F
y
Vx
Mx
C
A
550 lbf
B
z
=0⇒
400x − 550( x − 18) − 150( x − 42) + M x = 0
Trecho BD
150 lbf
∴ Vx = 300
∑M
Nx
= 0 ⇒ −400 − Vx + 550 + 150 = 0
∴ M x = 300x − 16200
Resposta: Com as equações (acima) podemos traçar os diagramas (abaixo). Note que os momentos
negativos foram traçados para cima.
300
V
150
-400
-7200
-3600
M