Trigonometria no Triângulo Retângulo e Medidas de arcos e

Trigonometria no Triângulo Retângulo e
Notas de Aula 02 –
Medidas de arcos e ângulos na circunferência Semestre 2 - 2010
Tópicos Fundamentais de Matemática - Licenciatura em Matemática –
Osasco -2010
Triângulo Retângulo
São triângulos nos quais algum dos ângulos internos é reto. O maior dos lados
de um triângulo retângulo é “oposto” ao vértice onde se encontra o ângulo reto
e á chamado de hipotenusa. Os outros dois lados menores são chamados de
catetos.
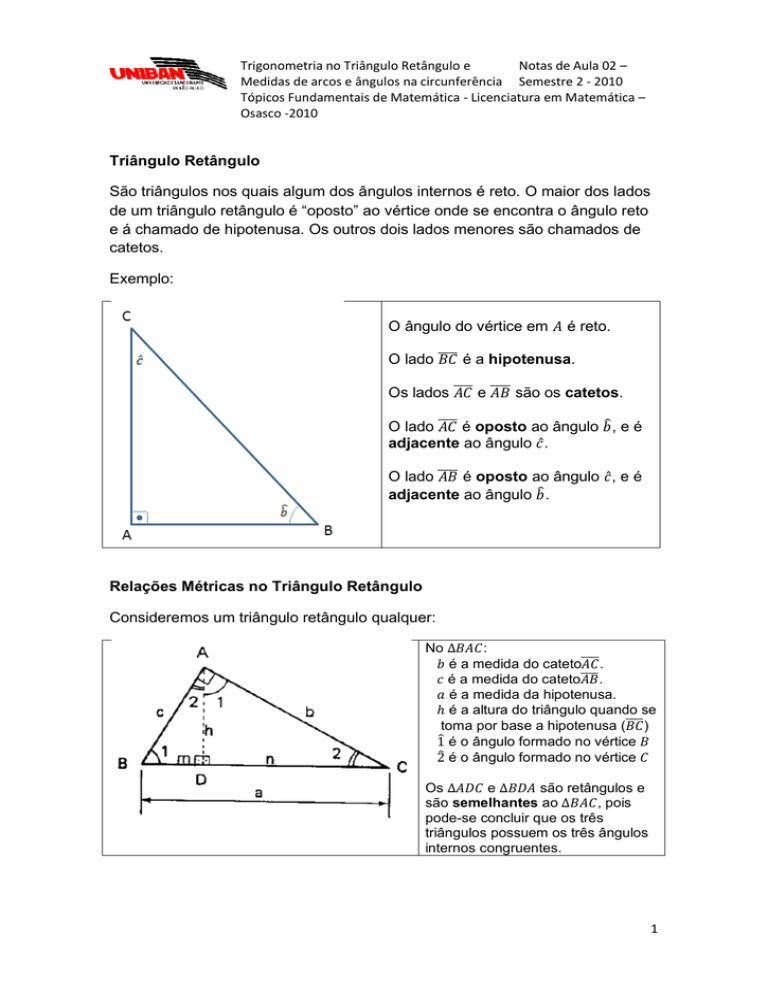
Exemplo:
O ângulo do vértice em
O lado
é reto.
é a hipotenusa.
Os lados
e
são os catetos.
O lado
é oposto ao ângulo , e é
adjacente ao ângulo .
O lado
é oposto ao ângulo , e é
adjacente ao ângulo .
Relações Métricas no Triângulo Retângulo
Consideremos um triângulo retângulo qualquer:
No
:
é a medida do cateto .
é a medida do cateto .
é a medida da hipotenusa.
é a altura do triângulo quando se
toma por base a hipotenusa ( )
é o ângulo formado no vértice
é o ângulo formado no vértice
Os
e
são retângulos e
são semelhantes ao
, pois
pode-se concluir que os três
triângulos possuem os três ângulos
internos congruentes.
1
Trigonometria no Triângulo Retângulo e
Notas de Aula 02 –
Medidas de arcos e ângulos na circunferência Semestre 2 - 2010
Tópicos Fundamentais de Matemática - Licenciatura em Matemática –
Osasco -2010
Pela semelhança dos triângulos
,
,e
, temos as seguintes relações
entre as medidas:
Como
Como
Como
, o que implica que o produto dos catetos é igual ao produto da altura pela
hipotenusa.
Como
Teorema de Pitágoras
Das relações (1) e (2) acima, temos
Mas,
Então
Concluímos,
Trigonometria no Triângulo Retângulo
2
Trigonometria no Triângulo Retângulo e
Notas de Aula 02 –
Medidas de arcos e ângulos na circunferência Semestre 2 - 2010
Tópicos Fundamentais de Matemática - Licenciatura em Matemática –
Osasco -2010
Se tomarmos vários triângulos retângulos semelhantes, digamos
,...,
, podemos dispô-los conforme a figura abaixo:
,
Ao tomarmos os triângulos deste conjunto, por semelhança de triângulos
teremos que :
Ou seja, a razão entre o cateto oposto a um determinado ângulo e a
hipotenusa de um triângulo retângulo é sempre constante. A esta razão
chamamos de “seno” do ângulo e representamos por
.
Também por semelhança de triângulos teremos que :
Ou seja, a razão entre o cateto adjacente a um determinado ângulo e a
hipotenusa de um triângulo retângulo é sempre constante. A esta razão
chamamos de “cosseno” do ângulo e representamos por
.
Também por semelhança de triângulos teremos que :
Ou seja, a razão entre o cateto oposto a um determinado ângulo e o cateto
adjacente ao mesmo ângulo de um triângulo retângulo é sempre constante. A
esta razão chamamos de “tangente” do ângulo e representamos por
.
Ainda por semelhança de triângulos teremos que :
3
Trigonometria no Triângulo Retângulo e
Notas de Aula 02 –
Medidas de arcos e ângulos na circunferência Semestre 2 - 2010
Tópicos Fundamentais de Matemática - Licenciatura em Matemática –
Osasco -2010
Ou seja, a razão entre o cateto adjacente a um determinado ângulo e o
cateto oposto ao mesmo ângulo de um triângulo retângulo é sempre constante.
A esta razão chamamos de “cotangente” do ângulo e representamos por
.
Resumindo :
Dado um triângulo retângulo qualquer de ângulos internos
sempre que:
e , teremos
Das relações acima concluímos diretamente que o seno de um ângulo é igual
ao cosseno de seu complementar , o cosseno de um ângulo é igual ao seno de
seu complementar, e que a tangente de um ângulo é igual a cotangente (ou ao
inverso da tangente) de seu complementar.
Lembrando: Ângulos complementares são aqueles cuja soma das medidas
resulta em um ângulo reto.
4
Trigonometria no Triângulo Retângulo e
Notas de Aula 02 –
Medidas de arcos e ângulos na circunferência Semestre 2 - 2010
Tópicos Fundamentais de Matemática - Licenciatura em Matemática –
Osasco -2010
Então,
Razões Trigonométricas para alguns ângulos Notáveis
Consideramos os valores de
, comovalores de ângulos
notáveis, para os quais os valores de Seno, Cosseno e Tangente estão listados
na tabela abaixo.
Medida do
âgulo (em
graus)
seno
cosseno
tangente
cotangente
Não há
Não há
Observação:


como a medida dos catetos nunca excede a medida da hipotenusa de
um triângulo retângulo, os valores de seno e cosseno dos ângulos
internos ao triângulo nunca excedem o valor de 1.
Note que quanto temos ângulos internos de
, não temos
triângulos de fato, mas podemos estender o cálculo do seno e cosseno
para estes casos.
5
Trigonometria no Triângulo Retângulo e
Notas de Aula 02 –
Medidas de arcos e ângulos na circunferência Semestre 2 - 2010
Tópicos Fundamentais de Matemática - Licenciatura em Matemática –
Osasco -2010
Encontrando o valor de um ângulo a partir do valor de uma razão
trigonométrica.
Se pensarmos em estabelecer uma relação entre o conjunto dos ângulos
no intervalo
e o conjunto dos números reais, veremos que tal relação é
uma função injetora. Portanto, pode-se estabelecer uma “função inversa” pela
qual, a partir de uma valor dado de
, podemos encontrar o valor de .
Sendo assim definimos para os ângulos internos de um triângulo
retângulo que :
Se
, então
, e se
, então
.
Ou seja,
Da mesma forma definimos:
e
Exemplos:
Medidas de Arcos de Circunferência
Um arco de circunferência é a curva que temos que percorrer sobre uma
circunferência para sairmos de um ponto A sobre ela e atingirmos um ponto B
sobre ela. Abaixo estão exemplificados os arcos
,e
6
Trigonometria no Triângulo Retângulo e
Notas de Aula 02 –
Medidas de arcos e ângulos na circunferência Semestre 2 - 2010
Tópicos Fundamentais de Matemática - Licenciatura em Matemática –
Osasco -2010
Note que, dados dois pontos sobre uma circunferência há duas possibilidades
para traçarmos arcos ligando estes dois pontos.
O Radiano
O radiano (símbolo rad) é um arco unitário cujo comprimento é igual ao raio da
circunferência que contém o arco a ser medido. Abaixo exemplificamos um
arco
de medida igual a 1 radiano.
Sabemos que a razão entre o diâmetro de uma circunferência e seu perímetro
é sempre igual a 3,1415927..., que é um número irracional que chamamos de
. Ou seja, se chamado de C o comprimento da circunferência, temos
Então, pela forma como definimos radianos, dizemos que um arco de
circunferência completo (ou simplemente uma circunferência) terá sempre o
comprimento de
rad.
A correspondência entre radianos e graus
Estabelecemos a seguinte correspondência para a conversão de unidades de
medida de arco de circunferência:
Medidas de arcos e ângulos
7
Trigonometria no Triângulo Retângulo e
Notas de Aula 02 –
Medidas de arcos e ângulos na circunferência Semestre 2 - 2010
Tópicos Fundamentais de Matemática - Licenciatura em Matemática –
Osasco -2010
Dado um ângulo
, consideremos uma circunferência de centro e raio .
Sejam
e
os pontos onde os lados do ângulo
intercepta a
circunferência traçada.
Fazendo construções desta forma, a cada arco
corresponderá um único
ângulo
. Convencionando que a um arco unitário corresponde um ângulo
central unitário, decorre que o arco
e o ângulo central
correspondente
passam a ter a mesma medida.
Comprimento de arcos de circunferência
Da forma como definimos, dado um arco de circunferência medido em
radianos, sabemos que cada radiano corresponde a um carco cujo
comprimento é
( o raio da circunferência). Então, dado o raio da
circunferência e a medida do arco dada em radianos, o comprimento do arco
da circunferência ( ) será dado por:
.
8
Trigonometria no Triângulo Retângulo e
Notas de Aula 02 –
Medidas de arcos e ângulos na circunferência Semestre 2 - 2010
Tópicos Fundamentais de Matemática - Licenciatura em Matemática –
Osasco -2010
Exercícios
1)Calcular o valor da hipotenusa e da altura em relação à hipotenusa num
triângulo retângulo cujos catetos medem 3 e 4.
Resposta: medida da hipotenusa
.
Altura em relação à hipotenusa
.
2)Calcule as medidas x,y,z e t, no triângulo abaixo:
Resposta:
.
3)Calcular a área de um triângulo retângulo em que as projeções dos
catetos sobre a hipotenusa medem, respectivamente,
e
.
Resposta:
.
4)Qual é a hipotenusa de um triângulo retângulo de perímetro 56 e altura
igual a
.
Resposta: 25
5)A figura mostra um edifício que tem 15 m de altura, com uma escada
colocada a 8 m de sua base ligada ao topo do edifício. Calcule o
comprimento dessa escada.
9
Trigonometria no Triângulo Retângulo e
Notas de Aula 02 –
Medidas de arcos e ângulos na circunferência Semestre 2 - 2010
Tópicos Fundamentais de Matemática - Licenciatura em Matemática –
Osasco -2010
6)Na figura tem-se que AB  BC e F é ponto médio do lado BE do retângulo
BCDE.
Qual é a área do retângulo
BCDE?
7)Aplicando as relações métricas nos triângulos retângulos abaixo,
determine o valor de x:
a)
b)

b
6
n
12
c)
3
d)

2 6


b
c
y
9
h
2
3
x
4
a
8)Com base no triângulo abaixo, assinale a alternativa correta.
10
Trigonometria no Triângulo Retângulo e
Notas de Aula 02 –
Medidas de arcos e ângulos na circunferência Semestre 2 - 2010
Tópicos Fundamentais de Matemática - Licenciatura em Matemática –
Osasco -2010
9)Assinale a opção correta dentre as alternativa abaixo.
10)O ângulo de elevação do pé de uma árvore, a 50 m da base de uma
encosta, ao topo da encosta é de 60º. Que medida deve ter um cabo
para ligar o pé da árvore ao topo da encosta?
11)Dois observadores se postavam de maneira que um deles pudesse ver o
barco sob um ângulo de 90º com relação à linha da costa e o outro sob
um ângulo de 45º. Qual deve ser a distância entre o barco e costa, se a
distância entre os observadores é igual a 50 metros?
12)Um barco parte de A para atravessar um rio. A direção de seu
deslocamento forma um ângulo de 120º com a margem do rio. Sendo a
largura do rio 60 m, qual a distância AB percorrida pelo barco na viagem
que faz de uma margem à outra?
13)Calcular os ângulos internos de um triângulo retângulo no qual os
catetos medem 9 e 12 cm. Obs: Se não encontrar valores notáveis para
as relações trigonométricas dê a resposta em função da “relação
trigonométrica inversa.
Resposta: Os dois ângulos internos medem
e
.
14)Calcular os lados de um triângulo retângulo cuja altura em relação à
hipotenusa é 4 e um dos ângulos é
.
Resposta: hipotenusa=
. Catetos:
e .
11
Trigonometria no Triângulo Retângulo e
Notas de Aula 02 –
Medidas de arcos e ângulos na circunferência Semestre 2 - 2010
Tópicos Fundamentais de Matemática - Licenciatura em Matemática –
Osasco -2010
15)Calcule os ângulos de um triângulo retângulo de hipotenusa 20,
sabendo que a mediana relativa a um dos catetos mede 15. Obs: Se não
encontrar valores notáveis para as relações trigonométricas dê a
resposta em função da “relação trigonométrica inversa.
Lembrete: a mediana de um triângulo é a reta que liga um vértice deste
triângulo ao ponto médio do lado oposto a este vértice.
Resposta:
e
16) (FFCLUSP – 66)
Na figura ao lado, os ângulos
e
, i= 1,2,... são
retos. Quanto vale a soma dos
segmentos
,
,
...em
função da medida de
(
) e de ?
Resposta:
17)Calcular o ângulo formado pela diagonal e o menor lado de um
retângulo cujos lados estão na razão
. Se não encontrar valores
notáveis para as relações trigonométricas dê a resposta em função da
“relação trigonométrica” inversa.
Resposta:
.
18)Calcular a área de um triângulo isóceles
.
Resposta:
cuja base mede 2 e
.
12
Trigonometria no Triângulo Retângulo e
Notas de Aula 02 –
Medidas de arcos e ângulos na circunferência Semestre 2 - 2010
Tópicos Fundamentais de Matemática - Licenciatura em Matemática –
Osasco -2010
19) Um observador vê o topo de um prédio, construído em um terreno
plano, sob um ângulo de
. Afatando-se do edifício mais 30 metros,
ele passa a ver o topo do prédio sob um ângulo de
. Qual é a altura
do prédio?
Resposta:
metros.
20)A partir de um ponto, observa-se o topo de um prédio sob um ângulo de
30º. Caminhando 24 m em direção ao prédio, atingimos outro ponto, de
onde se vê o topo do prédio segundo um ângulo de 60º. Desprezando a
altura do observador, calcule, em metros, a altura do prédio.
21)Para medir a altura de um prédio, um agrimensor sobe ao seu topo e
avista a base de uma árvore sob um ângulo de depressão de 30º(ver
figura). Em seguida, mede a distância do prédio à árvore e registra
120√3m. Qual é a altura do prédio?
13
Trigonometria no Triângulo Retângulo e
Notas de Aula 02 –
Medidas de arcos e ângulos na circunferência Semestre 2 - 2010
Tópicos Fundamentais de Matemática - Licenciatura em Matemática –
Osasco -2010
22)Para obter a altura H de uma chaminé, um engenheiro, com um
aparelho especial, estabeleceu a horizontal AB e mediu os ângulos e
tendo a seguir medido BC=h. Qual é a altura da chaminé em função
de
eh?
Resposta:
23)A seguir está representado um esquema de uma sala de cinema, com o
piso horizontal. De quanto deve ser a medida aproximada de AT para
que um espectador sentado a 15 metros da tela, com os olhos 1,2
metros acima do piso, veja o ponto mais alto da tela, que é T, a 30° da
horizontal?
24) Converter para radianos
a.
(Resposta: )
b.
(Resposta: )
c.
(Resposta: )
d.
(Resposta: )
e.
(Resposta:
)
14
Trigonometria no Triângulo Retângulo e
Notas de Aula 02 –
Medidas de arcos e ângulos na circunferência Semestre 2 - 2010
Tópicos Fundamentais de Matemática - Licenciatura em Matemática –
Osasco -2010
25) Converter para Graus
a.
(Resposta:
)
b.
(Resposta:
)
c.
(Resposta:
)
d.
(Resposta:
)
e.
(Resposta:
)
26) Transforme
em radianos e
Resposta:
,e
radianos em graus.
.
27)Converter para radianos:
a.
(Resposta: )
b.
(Resposta:
)
28)Qual é a medida, em radianos, de um arco de 20 cm de comprimento
contido numa circunferência de raio igual a 8 cm ?
Resposta: 2,5 radianos.
29)Um arco de circunferência mede 30 cm e o raio da circunferência mede
10 cm. Calcular a medida do arco em radianos.
Resposta: 3 rad.
30)Qual é o comprimento de um arco correspondente a um ângulo de
contido numa circunferência de raio igual a 1 cm ?
Resposta: cm.
,
31)O ponteiro dos minutos de um relógio mede 10 cm. Qual é a distância
que sua extremidade percorre em 30 minutos?
Resposta: Aproximadamente 31,4 cm.
32) Calcular a medida do ângulo central que um arco de comprimento
determina em uma circunferência de raio .
Resposta:
15
Trigonometria no Triângulo Retângulo e
Notas de Aula 02 –
Medidas de arcos e ângulos na circunferência Semestre 2 - 2010
Tópicos Fundamentais de Matemática - Licenciatura em Matemática –
Osasco -2010
33)Calcular o menor dos ângulos formados pelos ponteiros de um relógio
que está marcando:
a. 1 h (Resposta: )
b. 1 h 15 min (Resposta:
c. 1 h 40 min. (Resposta:
)
)
Referências
Dante, L. Roberto. Matemática: Contexto e aplicações. Volume 1. Ed. 3.
Impressão 1. Editora Ática. São Paulo.2003.
Iezzi, Gelson (e outros). Fundamentos de Matemática Elementar. Volume
3. Ed Atual. São Paulo. 1977.
16