Lista de Exercícios 2 - Gabriel Mendes (1º Ano)

2
seja de 72cm , calcule o comprimento dolado
do quadrado maior.
Quadriláteros Notáveis
7. Um estudante fez a seguinte afirmação:
“Um trapézio que tem dois ângulos
consecutivos é isósceles”. Este estudante
acertou? Em caso positivo, mostre a
afirmação e em caso negativo dê um
contra-exemplo.
1. O perímetro de um losango é 80cm. Se
uma de suas diagonais é o triplo da outra, qual
a medida da diagonal maior?
8. (Fuvest) Na figura, os quadrados ABCD e
EFGH têm, ambos, lado L e centro O. Se
EP=1, então L é:
Lista de Exercícios 2 Gabriel Mendes (1º Ano)
2. Obtenha o perímetro de um losango cujas
diagonais medem 2cm e 4cm.
3. Os ângulos internos de um quadrilátero
medem 3x-45º, 2x+10º, 2x+15º e x+20º. O
menor ângulo mede?
a) 90º
b) 65º
c) 46º
d) 105º
e) 80º
4. (FGV) Na figura a seguir, ABCD é retângulo
e AMCN é um losango. Determine a medida
do
segmento
NB
sabendo
que
AB=2AD=20cm.
√ 2/(√ 2-1)
b) 2/(√ 3-1)
a)
c)
√ 2/2
e)
√ 2/(√ 2-1)
d) 2
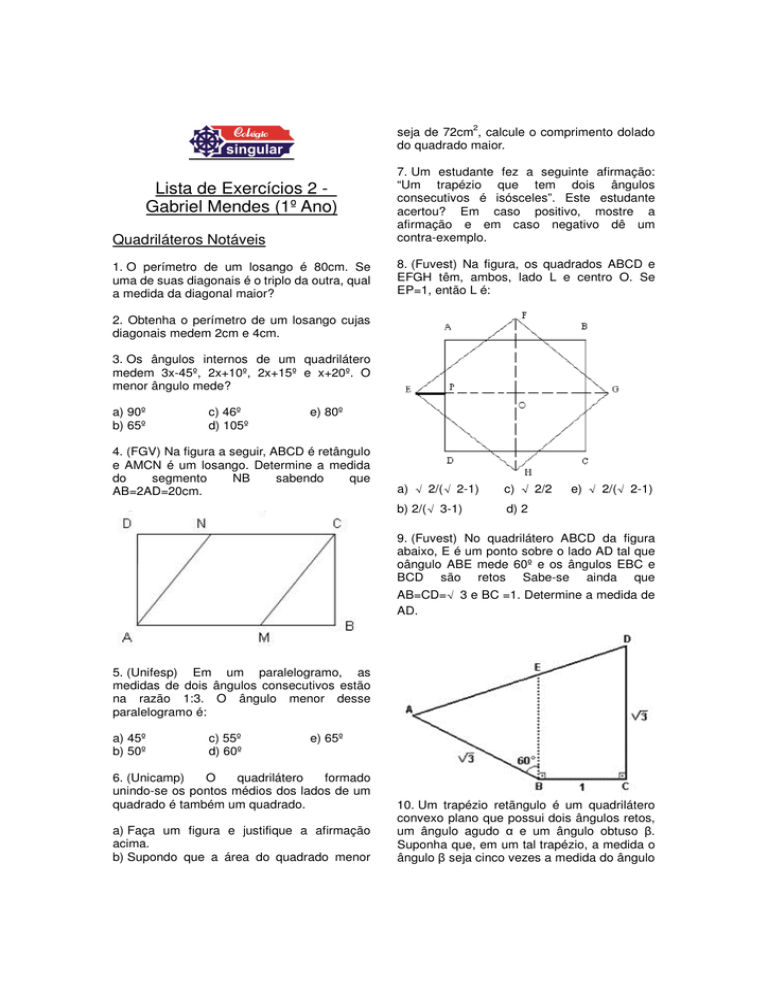
9. (Fuvest) No quadrilátero ABCD da figura
abaixo, E é um ponto sobre o lado AD tal que
oângulo ABE mede 60º e os ângulos EBC e
BCD são retos Sabe-se ainda que
AB=CD=√ 3 e BC =1. Determine a medida de
AD.
5. (Unifesp) Em um paralelogramo, as
medidas de dois ângulos consecutivos estão
na razão 1:3. O ângulo menor desse
paralelogramo é:
a) 45º
b) 50º
c) 55º
d) 60º
e) 65º
6. (Unicamp)
O
quadrilátero
formado
unindo-se os pontos médios dos lados de um
quadrado é também um quadrado.
a) Faça um figura e justifique a afirmação
acima.
b) Supondo que a área do quadrado menor
10. Um trapézio retãngulo é um quadrilátero
convexo plano que possui dois ângulos retos,
um ângulo agudo α e um ângulo obtuso β.
Suponha que, em um tal trapézio, a medida o
ângulo β seja cinco vezes a medida do ângulo
α.
a) Calcule a medida de α em graus.
b) Mostre que o ângulo formado
bissetrizes de α e β é reto.
pelas
11. (Fuvest) Um trapézio retângulo tem bases
5 e 2 e altura 4. O perímetro desse trapézio é:
a) 13
b) 14
c) 15
d) 16
e) 17
12. (Fuvest) No retângulo a seguir, o valor em
graus de α+β é:
a) 50º
b) 90º
c) 120º
d) 130º
e) 220º
13. Considerando que S e R são os pontos
médios dos lados correspondentes do
trapézio ABCD abaixo, determine x e y (Dica:
lembre do teorema da base média dos
triângulos)
15. Em um paralelogramo ABCD, AB=2x+1,
BC=3x+4, CD=9, AD=y+1. Calcule os valores
de x e y.
16. A figura abaixo mostra o trapézio ABCD.
Sabendo que P, Q, R e S são os pontos
médios das diagonais AC e BD e dos lados
BC e AD, respectivamente, determine as
medidas de SP, PQ e QR (o desenho está fora
de escala).
17. Em um losango, uma das diagonais faz
um ângulo de 50º com um de seus lados. Os
ângulos internos desse losango medem:
a) 50º e 40º
b) 120º e 60º
c) 110º e 70º
d) 100º e 80º
e) 90º e 90º
Pontos Notáveis num Triângulo
18. Um ponto P equidista dos vértices de um
triângulo ABC. O ponto P é:
a) O baricentro do triângulo ABC
b) O incentro do triângulo ABC
c) O circuncentro do triângulo ABC
d) O ortocentro do triângulo ABC
e) Nenhuma das anteriores
19. Qual dos pontos notáveis de um triângulo
pode ser um de seus vértices?
14. Sabe-se que a base média de um trapézio
é a soma da base maior com a base menor
divindo o resultado por 2. A base média de um
trapézio mede 60cm e a base menor é igual a
3/7 da base maior. A medida dessas bases é,
em cm, respectivamente:
a) 90 e 40
b) 74 e 23
c) 84 e 36
d) 92 e 46
e) 86 e 37
a) Baricentro
b) Incentro
c) Ortocentro
d) Circuncentro
e) Nenhum
20. Quais pontos notáveis de um triângulo
nunca se posicionam externemente em
relação a sua região triangular?
a) Baricentro e Ortocentro
b) Incentro e Circuncentro
c) Baricentro e Circuncentro
d) Incentro e Ortocentro
e) Baricentro e Incentro
21. (Unitau) O segmento da perpendicular
traçada de um vértice de um triângulo à reta
suporte do lado oposto é denominado:
a) Mediana
b) Mediatriz
c) Bissetriz
d) Altura
25. Na figura abaixo, I é o incentro do triângulo
ABC. Sendo AB=9cm, AC=12cm e BC=7cm,
calcule a razão AI/DI.
e) Base
22. (Fuvest) Um triângulo ABC tem ângulos
A=40º e B=50º. Qual é o ângulo formado
pelas alturas relativas ao vértice A e B desse
triângulo?
a) 30º
b) 45º
c) 60º
d) 90º
e) 120º
23. (Ufpi) No triângulo ABC (figura abaixo), os
lados AB e AC medem respectivemente 5cm e
7cm. Se O é o incentro do triângulo ABC e o
segmento MN é paralelo a BC então o
perímetro do triângulo AMN é:
26. Qual a distância entre o circuncentro e o
baricentro de um triângulo retângulo cujos
catetos medem 5cm e 12cm? (Dica: lembre-se
do acontece nos triângulos retângulos
inscritos em uma circunferência).
27. Seja ABC um triângulo isósceles, com
AB=AC. Seja I o incentro desse triângulo. Se
AI = 3cm e a distância de I até BC é 2cm,
determine a medida do lado BC.
28. Em um triângulo equilátero podemos
determinar a altura deste triângulo pela
expressão h=(L√ 3)/2 onde L é o lado deste
triângulo. Assim, responda as seguintes
perguntas:
a) Mostre que o raio da circunferência inscrita
no triângulo pode ser calculado pela
a) 8
b) 9
c) 10
d) 11
e) 12
24. Na figura abaixo, AB=AC e O é o incentro
do triângulo ABC e o ângulo BÔC é o triplo do
ângulo Â. Então a medida de  é:
a) 18º
b) 12º
c) 24º
d) 36º
e) 15º
expressão r = (L√ 3)/6. (Dica: lembre-se que
em um triângulo equilátero todos os centros
são o mesmo).
b) Mostre que o raio da circunferência
circunscrita ao triângulo pode ser calculado
pela fórmula R = (2L√ 3)/3.
c) Mostre que a área de um triângulo
equilátero pode ser calculada pela fórmula
A = (L2√ 3)/4. (Dica: lembre-se que a área de
um triângulo é dada por base vezes a altura
dividido por 2).
29. Utilize o exercício anterior para calcular os
raios das circunferências inscrita e circunscrita,
a altura e a área de um triângulo equilátero
cujo lado mede
√ 6 cm.
32. (FGV) Na figura, ABC é um triângulo com
AC=20cm, AB=15cm e BC=14cm. Sendo AQ
e BP bissetrizes interiores do triângulo ABC, o
quociente QR/AR é igual a:
Teorema de Tales e Semelhança
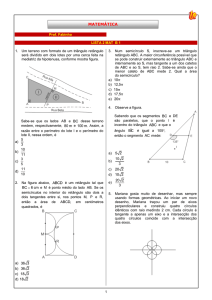
30. Para a instalação de luz elétrica no
quarteirão de um loteamento, serão colocados
quatro postes, A, B, C e D, como indica a
figura abaixo. Sabendo-se que as laterais do
terreno são paralelas e a distância AD
corresponde a 180m, é certo afirmar que a
distância entre os postes A e B corresponde a:
a) 0,3
b) 0,35
c) 0,4
d) 0,45
e) 0,5
33. (Mack) Na figura temos r//r’ e s //s’. Então,
para todo valor a>1 o valor da abcissa x é:
a) 50m
b) 52m
c) 54m
d) 56m
e) 58m
31. Na figura a seguir, ABCD é um retângulo e
PQ é a bissetriz interna do ângulo P do
triângulo DPC. Sabe-se que AD=DQe que as
medidas estão indicadas em centímetros.
Qual é o perímetro do retângulo ABCD?
a) 2a
b) a2
c) (a+1)
d) a+1
2
e)
√ a+1
34. (Fuvest) Um triângulo ABC tem lados de
comprimento AB=5, BC=4 e AC=2. Sejam M e
N os pontos AB tais que CM é a bissetriz
relativa ao lângulo ACB e CN é a altura
relativa ao lado AB. Determinar o
comprimento de MN.
35. No triângulo ABC, o lado AC e a mediatriz
do segmento BCse encontram no ponto D, e a
reta BD é bissetriz e ABC. Se AD=9 e DC=7,
qual a área do triângulo ABD?
a) 14
c) 28
e) 28√ 5
b) 21
d) 14√ 5
36. (Fuvest) A sombra de um poste vertical,
projetada pelo sol re um chão plano, mede
12m. Nesse mesmo instante, a sombra de um
bastão vertical de 1m de altura mede 0,6m. A
altura do poste é:
a) 6m
b) 7,2m
c) 12m
d) 20m
e) 72m
38. (UFRGS) Para estimar a profundidade de
um poço com 1,10m de largura, uma pessoa,
cujos olhos estão a 1,60m do chão
posiciona-se a 0,5m de sua borda. Dessa
forma a borda do poço esconde exatamente
seu fundo, como mostra a figura abaixo. Com
os dados acima, a pessoa conclui que a
profundidade do poço é de:
a) 2,82m
b) 3,00m
c) 3,30m
d) 3,52m
a) 3
b) 4
c) 5
d) 6
e) 7
39. O triângulo ABC tem altura h e base b (ver
figura). Nele, está inscrito o retângulo DEFG,
cuja base é o dobro da altura. Nessas
condições, a altura do retângulo em função de
h e b, é dada pela fórmula:
e) 3,85m
a) bh/(h+b)
b) bh/(2h+b)
38. (Fuvest) Na figura abaixo, as distâncias
dos pontos A e B à reta r valem 2 e 4. As
projeções ortogonais de A e B sobre essa reta
são os pontos C e D. Se a medida de CD é 9,
a que distância de C deverá estar no ponto E,
do segmento CD, para que CEA=DEB?
c) 2bh/(h+b)
d) bh/2(h+b)
e) bh/(h+2b)
40. (Fuvest) No triângulo acutângulo ABC, a a
base AB mede 4cm e a altura relativa a essa
base também mede 4cm. MNPQ é um
retângulo cujos vértices M e N pertencem ao
lado AB, P pertence ao lado BC e Q pertence
ao lado AC. O perímetro desse retãngulo em
centímetros é:
cujo assento tem forma retangular, de
comprimento 40cm, apóia-se sobre duas
barras iguais de comprimento 60cm (ver
figura). Cada barra tem três furos e o ajuste de
altura do banco é feito colocando-se o
parafuso nos primeiros, segundos ou terceiros
furos das barras (ver visão lateral do banco na
figura 2). A menor altura que pode ser obtida
é:
a) 4
b) 8
c) 12
d) 14
e) 16
41. (Fuvest) Na figura, o triângulo ABC é
retângulo em A , ADEF é um quadrado, AB=1e
AC=3. Quanto mede o lado do quadrado?
a) 0,7
b) 0,75
c) 0,8
d) 0,85
a) 36
c) 40
e) 44
b) 38
d) 42
44. (UEL) Após um tremor de terra, dois
muros paralelos em uma rua de uma cidade
fcaram ligeiramente abalados. Os moradores
se reuniram e decidiram escorar os muros
utilizando duas barras metálicas, como mostra
a figura abaixo. Sabendo que os muros tem
alturas de 9m e 3m, respectivamente, a que
altura do nível do chão as duas barras se
interceptam? Despreze a espessura das
barras.
e) 0,9
42. (Fuvest) Na figura abaixo, ABC é um
triângulo isósceles e e retângulo em A e
PQRS é um quadraddo de lado 2√ 2/3. Então
a medida do lado AB é:
(figura)
a) 1
b) 2
c) 3
d) 4
e) 5
43. (Fuvest) Um banco de altura regulável,
a) 1,5m
b) 1,75m
c) 2,00m
d) 2,25m
e) 2,5m
45. (Fuvest) A figura representa um retângulo
ABCD, com AB=5 e AD=3. O ponto E está no
segmento CD de maneira que CE=1 e F é o
ponto de intersecção da diagonal AC com o
segmento BE. Então a área do triângulo BCF
vale:
os pontos re BA e BC, respectivamente, de
modo que a reta PQ seja paralela à reta AC e
a área do trapézio APQC seja o triplo da área
do triângulo PQB.
a) Qual a razão entre as áreas dos triângulos
ABC e PQB?
b) Determine a razão AB/PB.
48. (Fuvest) Em uma mesa de bilhar,
coloca-se uma bola branca na posição B e
uma bola vermelha na posição V, conforme o
esquema abaixo. Deve-se jogar a bola branca
de modo que ela siga a trajetória indicada na
figura e atinja a bola vermelha. Assumindo
que, em cada colisão da bola branca com a
mesa, os ângulos de incidência e de reflexão
são iguais, a que distância x do vértice Q
deve-se jogar a bola branca?
a) 6/5
b) 5/4
c) 4/3
d) 7/5
e) 3/2
46. (Fuvest) Um lateral L faz um lançamento
para um atacante A, situado 32m à sua frente
em uma linha paralela à lateral do campo de
futebol. A bola, entretanto, segue uma
trajetória retilínea, mas não paralela à lateral e
quando passa pela linha de meio de
campoestá a uma distância de 12m da linha
que une o lateral ao atacante. Sabendo-se
que a linha de meio de campo está à mesma
distância dos dois jogadores, a distância
mínima que o atacante terá que percorrer para
encontrar a trajetória da bola será de:
49. (UFRGS) Considere a figura abaixo. Se os
retângulos ABCD e BCEF são semelhantes, e
AD=1, AF=2 e FB=x, então x vale:
a) 18,8
b) 19,2
c) 19,6
d) 20
e) 20,4
47. (Fuvest) Num triângulo ABC sejam P e Q
a) -1+√ 2
b) 1
√ 2
d) 1+√ 2
c)
e) 2
50. (Fuvest) Na figura, ABCD é um quadrado
de 6cm de lado, M é o ponto médio do lado
DC e A é o ponto médio de PC. Calcule a área
do triângulo MDN.
Desafios
51. Sejam ABCD um quadrado, E ponto médio
de CD e M interior ao quadrado. Sabendo que
MAB=MBC=EMB=x, determine x. (Dica: use
que, em um triângulo retângulo, a mediana
relativa à hipotenusa mede metade da
hipotenusa).
52. Seja ABC um triângulo tal que AB=AC e
que BAC=20º, como na figura. Determine
CPQ.
53. P é um ponto interior ao quadrado ABCD
tal que PA=1, PB=2 e PC=3. Determine APB.
54. (Ita) Considere o triângulo ABC, onde AD
é a mediana relativa ao lado BC. Por um ponto
arbitrário M do segmento BD, tracemos o
segmento MP paralelo a AD, onde P é o ponto
de intersecção desta paralela com o
prolongamento do lado AC (figura). Se N é o
ponto de intersecção de AB com MP, podemos
afirmar que:
Respostas
1. 6√ 2
2. 4√ 5
3. B
4. (5√ 41)/2
5. A
6. a) Basta desenhar e aplicar o teorema de
pitágoras
b) 12cm
7. Não. O contra-exemplo fica para vocês
pensarem.
8. E
a) MN+MP=2BM
b) MN+MP=2CM
c) MN+MP=2AB
d) MN+MP=2AD
e) MN+MP=2AC
55. (Olímpiada Mexicana) Na figura, ABC é
um triângulo equilátero e lado 3, e a reta PA é
paralela à reta BC. Sabendo que PQ=QR=RS,
então o comprimento do segmento CS é igual
a:
a) 1/3
b) 1/4
c) 1/5
d) 1
e) 2
“Deixem que o futuro diga a verdade e avalie
cada um de acordo com seu trabalho e
realizações. O presente pertence a eles, mas o
futuro pelo qual eu sempre trabalhei, pertence
a mim.”
Nikola Tesla
"So, I'm 40, I'm not married, I don't fly jets,
and I don't have a dog?...
...Why does the moon gets orange
sometimes?"
Disney's The Kid
9. √ 7
10. a) 30º
b) Lembre-se que bissetriz é uma
semirreta que divide um ângulo exatamente
na metade.
11. E
12. D
13. x=3 e y=4
14. C
15. x=4 e y=15
16. SP=QR=6cm e PQ=4cm
17. D
18. C
19. C
20. E
21. D
22. D
23. E
24. D
25. AI/DI=3
26. 13/6 cm
27. 4√ 5
28. Demonstrações.
√ 2/2 cm
R = 2√ 2 cm
h = 3√ 2/2 cm
A = 3√ 3/2
29. r =
30. C
31. 15,2 cm
32. C
33. B
34. 11/30
35. D
36. B
37. D
38. A
39. D
40. B
41. B
42. B
43. A
44. D
45. B
46. B
47. a) 4
b) 2
48. x=6/17m
49. A
2
50. 6cm
51. 75º
52. 30º
53. 135º
54. D
55. D
Civil War!!!