1 Trabalho de Recuperação Final - 1° Ano

Trabalho de Recuperação Final - 1° Ano - Ensino Médio
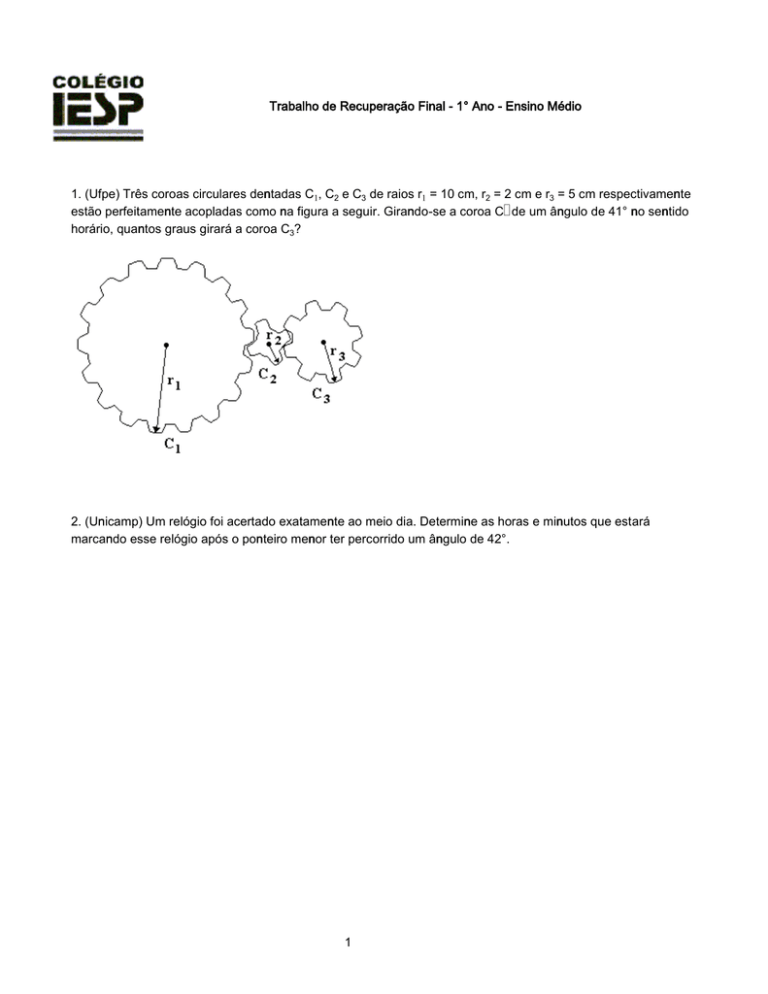
1. (Ufpe) Três coroas circulares dentadas C, C‚ e Cƒ de raios r = 10 cm, r‚ = 2 cm e rƒ = 5 cm respectivamente
estão perfeitamente acopladas como na figura a seguir. Girando-se a coroa C• de um ângulo de 41° no sentido
horário, quantos graus girará a coroa Cƒ?
2. (Unicamp) Um relógio foi acertado exatamente ao meio dia. Determine as horas e minutos que estará
marcando esse relógio após o ponteiro menor ter percorrido um ângulo de 42°.
1
3. (Unesp) Cinco cidades, A, B, C, D e E, são interligadas por rodovias, conforme mostra a figura.
A rodovia AC tem 40 km, a rodovia AB tem 50 km, os ângulos x, entre AC e AB, e y, entre AB e BC, são tais que
senx = 3/4 e seny = 3/7. Deseja-se construir uma nova rodovia ligando as cidades D e E que, dada a disposição
destas cidades, será paralela a BC.
a) Use a lei dos senos para determinar quantos quilômetros tem a rodovia BC.
b) Sabendo que AD tem 30 km, determine quantos quilômetros terá a rodovia DE.
4. (G1) Na figura seguinte identifique os pares de ângulos:
a) correspondentes
b) alternos internos
c) alternos externos
d) colaterais internos
e) colaterais externos
f) o.p.v.
g) adjacentes
2
5. (G1) Sendo r//s calcule o ângulo m. Justifique.
6. (G1) Na figura a seguir r//s e s//t. Nestas condições determine as medidas indicadas. Justifique.
7. (G1) Determine o valor de
4° 39' 45" + 18° 32' 43" + 8° - 7° 49"
3
8. (G1) Num triângulo isósceles ABC, cada ângulo da base mede 74° e cada lado congruente 8 cm. Nessas
condições determine: (use a tabela trigonométrica)
a) a medida da altura h.
b) a medida x da base do triângulo.
9. (G1) Determine o perímetro dos seguintes polígonos. (Dê a resposta em m).
a) Um triângulo equilátero de lado igual a 15 cm.
10. (G1) Determine o perímetro:
a) de um decágono regular de lado igual a 12 cm
b) de um triângulo equilátero de lado igual a 1,87 dm. Dê a resposta em metros.
4
11. (G1) Determine x:
12. (G1) O ângulo interno de um polígono regular é o triplo do ângulo externo. Qual é esse polígono?
13. (G1) A soma dos ângulos internos de um polígono regular é 1440°. Determine a medida do ângulo central.
14. (G1) Dois decágonos regulares são semelhantes e a razão de semelhança entre eles é 1/4. Se o perímetro do
menor mede 130 cm, quanto mede cada lado do maior decágono?
15. (Cesgranrio) Uma escada de 2 m de comprimento está apoiada no chão e em uma parede vertical. Se a
escada faz 30° com a horizontal, a distância do topo da escada ao chão é de:
a) 0,5 m
b) 1 m
c) 1,5 m
d) 1,7 m
e) 2 m
5
16. (Ufpe) Considere os triângulos retângulos PQR e PQS da figura a seguir.
Se RS = 100, quanto vale PQ?
a) 100Ë3
b) 50Ë3
c) 50
d) (50Ë3)/3
e) 25Ë3
17. (Unesp) A figura adiante representa o perfil de uma escada cujos degraus têm todos a mesma extensão, além
de mesma altura. Se åæ = 2 m e BðA mede 30°, então a medida da extensão de cada degrau é:
a) (2Ë3)/3 m
b) (Ë2)/3 m
c) (Ë3)/6 m
d) (Ë3)/2 m
e) (Ë3)/3 m
6
18. (Fuvest) Considere um arco AB de 110° numa circunferência de raio 10 cm. Considere, a seguir, um arco A'B'
de 60° numa circunferência de raio 5 cm.
Dividindo-se o comprimento do arco AB pelo do arco A'B' (ambos medidos em cm), obtém-se:
a) 11/6.
b) 2.
c) 11/3.
d) 22/3.
e) 11.
19. (Ufal) Se a medida de um arco, em graus, é igual a 128, sua medida em radianos é igual a
a) (™/4) - 17
b) (64/15) ™
c) (64/45) ™
d) (16/25) ™
e) (32/45) ™
20. (Ufc) Sabendo que cosš = (Ë3)/2 e que senš = - 1/2, podemos afirmar corretamente que
cos[(š + (™/2)] + sen[š + (™/2)]
é igual a:
a) 0
b) [-(Ë3)/2] - (1/2)
c) [(Ë3)/2] + (1/2)
d) [(Ë3)/2] - (1/2)
e) [-(Ë3)/2] + (1/2)
21. (Uflavras) Às 11 horas e 15 minutos, o ângulo ‘ (figura abaixo) formado pelos ponteiros de um relógio mede
a) 90°
b) 112° 30'
c) 82° 30'
d) 120°
e) 127° 30'
7
22. (Uflavras) A figura MNPQ é um retângulo inscrito em um círculo. Se a medida do arco AM é ™/4 rad, as
medidas dos arcos AN e AP, em radianos, respectivamente, são:
a) 3™/4 e 5™/4
b) ™ e 3™/2
c) 3™/4 e 2™
d) ™/2 e 5™/4
e) 3™/4 e 5™/8
23. (Ufrn) No protótipo antigo de uma bicicleta, conforme figura abaixo, a roda maior tem 55 cm de raio e a roda
menor tem 35 cm de raio. O número mínimo de voltas completas da roda maior para que a roda menor gire um
número inteiro de vezes é
a) 5 voltas.
b) 7 voltas.
c) 9 voltas.
d) 11 voltas.
8
24. (Ufrs) Os ponteiros de um relógio marcam duas horas e vinte minutos. O menor ângulo entre os ponteiros é
a) 45°
b) 50°
c) 55°
d) 60°
e) 65°
25. (Ufrs) Considere as seguintes afirmações para arcos medidos em radianos:
I) sen 1 < sen 3
II) cos 1 < cos 3
III) cos 1 < sen 1
Quais são verdadeiras?
a) Apenas I é verdadeira.
b) Apenas II é verdadeira.
c) Apenas III é verdadeira.
d) São verdadeiras apenas I e II.
e) São verdadeiras I, II e III.
26. (Ufrs) Se o ponteiro menor de um relógio percorre um arco de ™/12 rad, o ponteiro maior percorre um arco de
a) ™/6 rad.
b) ™/4 rad.
c) ™/3 rad.
d) ™/2 rad.
e) ™ rad.
27. (Ufrs) Dentre os desenhos abaixo, aquele que representa o ângulo que tem medida mais próxima de 1 radiano
é
9
28. (Ufscar) Se o ponteiro dos minutos de um relógio mede 12 centímetros, o número que melhor aproxima a
distância em centímetros percorrida por sua extremidade em 20 minutos é: (considere ™=3,14)
a) 37,7 cm.
b) 25,1 cm.
c) 20 cm.
d) 12 cm.
e) 3,14 cm.
29. (Ufscar) O gráfico em setores do círculo de centro O representa a distribuição das idades entre os eleitores de
uma cidade. O diâmetro åæ mede 10 cm e o comprimento do menor arco AC é (5™/3) cm.
O setor x representa todos os 8000 eleitores com menos de 18 anos, e o setor y representa os eleitores com idade
entre 18 e 30 anos, cujo número é
a) 12000
b) 14800
c) 16000
d) 18000
e) 20800
10
30. (Unb) O radar é um aparelho que usa o princípio da reflexão de ondas para determinar a posição de um objeto
que se encontra distante ou encoberto por nevoeiro ou nuvem. A posição do objeto é indicada sob a forma de um
ponto luminoso que aparece na tela do radar, que apresenta ângulos e círculos concêntricos, cujo centro
representa a posição do radar, conforme ilustra a figura abaixo.
Considere que os pontos A e B da figura sejam navios detectados pelo radar, o navio A está a 40 km do radar e o
navio B, a 30 km. Com base nessas informações e desconsiderando as dimensões dos navios, julgue os itens que
se seguem.
(1) A distância entre os navios A e B é maior que 69 km.
(2) Se, a partir das posições detectadas pelo radar, os navios A e B começarem a se movimentar no mesmo
instante, em linha reta, com velocidades constantes e iguais, o navio A para o leste e o navio B para o norte, então
eles se chocarão.
(3) A partir da posição detectada pelo radar, caso B se movimente sobre um círculo de raio igual a 30 km, no
sentido anti-horário, com velocidade constante de 40 km/h então, em 10 min, o navio B percorrerá um arco
correspondente a (40/™)°.
31. (Ita) Num triângulo acutângulo ABC, o lado oposto ao ângulo  mede 5cm. Sabendo que
 = arc cos 3/5 e ð = arc sen 2/Ë5,
então a área do triângulo ABC é igual a
a) 5/2 cm£.
b) 12 cm£.
c) 15 cm£.
d) 2Ë5 cm£.
e) 25/2 cm£.
11
32. (Cesgranrio) No triângulo ABC, os lados AC e BC medem 8 cm e 6 cm, respectivamente, e o ângulo A vale
30°.
O seno do ângulo B vale:
a) 1/2
b) 2/3
c) 3/4
d) 4/5
e) 5/6
33. (Fuvest) Na figura adiante, as retas r e s são paralelas, o ângulo 1 mede 45° e o ângulo 2 mede 55°. A medida,
em graus, do ângulo 3 é:
a) 50
b) 55
c) 60
d) 80
e) 100
12
34. Observe a figura a seguir e classifique em verdadeira ou falsa cada uma das afirmações:
a) (
b) (
c) (
d) (
e) (
f) (
g) (
h) (
i) (
j) (
)AÆr
) AE » EB = AB
) EB Å r
) AB e EB são segmentos colineares
) AE e EF são segmentos consecutivos
) r, s e t são retas paralelas
)rºs={F}
) CF » FD = CD
)tºs={E}
)EÆreEÅr
35. (Unaerp) As retas r e s são interceptadas pela transversal "t", conforme a figura. O valor de x para que r e s
seja, paralelas é:
a) 20°
b) 26°
c) 28°
d) 30°
e) 35°
13
36. (Faap) A medida mais próxima de cada ângulo externo do heptágono regular da moeda de R$ 0,25 é:
a) 60°
b) 45°
c) 36°
d) 83°
e) 51°
37. (Unitau) O polígono regular convexo em que o n¡. de lados é igual ao n¡. de diagonais é o:
a) dodecágono.
b) pentágono.
c) decágono.
d) hexágono.
e) heptágono.
38. (G1) Calcule a soma dos catetos do triângulo retângulo da figura, sabendo que AB = 10 e cos x = 3/5
a) 6
b) 8
c) 14
d) 2
e) 16
14
39. Para o triângulo retângulo BAC, a relação correta é:
a) sen ï = b/a
b) cos ï = b/a
c) tg ï = c/b
d) tg ð = b/c
e) sen ð = b/a
40. O valor de a no triângulo ABC é:
a) 32
b) 36
c) 30
d) 33
e) 34
15