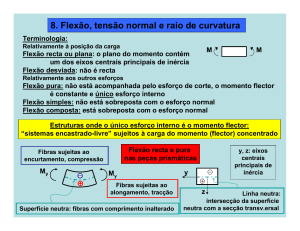
Flexão Composta

Flexão
Composta
ƒA
flexão composta é a ação combinada de
força normal e momentos fletores
ƒ Os
momentos fletores podem decorrer da
excentricidade, com relação ao eixo do
elemento, de força atuando na direção
longitudinal
Tipos de Flexão
Composta
1. Flexão Composta Reta
Ação combinada de força normal e apenas
um momento fletor, em relação ao eixo z (Mz)
ou em relação ao eixo y (My).
2. Flexão Composta Oblíqua
Ação combinada de força normal e dois
momentos fletores, em relação ao eixo z (Mz)
e em relação ao eixo y (My).
• Tensão normal relativa à força normal
Seção S
N
σx =
A
• Tensão normal relativa a Mz
Seção S
Mz
σx =
y
Iz
Linha neutra (L.N.)a lugar geométrico dos pontos onde σx =
Neste caso, a L.N. coincide com o eixo z que passa pelo
centróide da seção
0
• Tensão normal relativa a My
Seção S
σx = −
My
Iy
z
Neste caso, a L.N. coincide com o eixo y que passa
pelo centróide da seção
Estudo da Flexão
Composta
Na prática, a flexão composta ocorre freqüentemente em
pilares, em vigas protendidas, em muros de arrimo, etc.
O estudo da flexão composta deve ser feito com todas
as cargas reduzidas ao centróide da seção transversal.
Portanto,
F
M=F e
N
e
1- Pilares
• Carga longitudinal aplicada
sobre o eixo y
Tem-se então:
N e Mz
Flexão Composta Reta
F
• Carga longitudinal aplicada
sobre o eixo z
Tem-se então:
N e My
Flexão Composta Reta
F
• Carga longitudinal aplicada fora dos
dois eixos
F
Tem-se então:
N , Mz e My
Flexão Composta Oblíqua
2 - Viga Protendida
N e Mz
Flexão Composta Reta
Exercícios Resolvidos
1. Traçar diagrama de σx para uma
seção do pilar, admitindo-se e=20,0 cm
x
4000kN
z
z
80 cm
y
e
80 cm
y
Resolução:
1. Características da seção:
A = b × h = 800 × 800 = 640 × 10 3 mm 2
b × h3 800 × 8003
Iz =
=
= 3,41×1010 mm 4
12
12
2. Esforços solicitantes em todas as seções:
N = −4000 kN = −4 × 106 N
M z = −F × e
M z = −4 × 106 × 200 = −800 × 106 Nmm
3. Equação da Tensão Normal (σx):
(
)
− 4 × 106
N Mz
− 800 × 106
+
σx = +
y ⇒σx =
y
3
10
A Iz
640 × 10
3,41 × 10
⇒ σ x = −6,25 − 0,02344 y
Analisando essa equação, observa-se que σx só
depende de y.
y = distância do ponto onde se quer calcular a tensão
até o eixo z que passa pelo centróide da seção
4. Cálculo da Tensão Normal (σx):
Z
• Para y = +400mm, tem-se:
σ x = −6,25 − 0,02344 × (+ 400 )
Y
σ x = −15,63MPa
-400mm
• Para y = -400mm, tem-se:
σ x = −6,25 − 0,02344 × (− 400 )
σ x = +3,13MPa
+400mm
5. Posição da Linha Neutra:
Como a linha neutra é o lugar geométrico dos pontos
onde σx= 0, tem-se que:
σ x = −6,25 − 0,02344 y = 0
L.N.
∴ y = −267,1mm
z
y
− 267 ,1mm
6. Diagrama de Tensão Normal (σx):
-15,61MPa
+3,11MPa
L.N.
-15,61MPa
+3,11MPa
ou
-15,61MPa
+3,11MPa
2. Traçar diagrama de σx para uma
seção do pilar
x
950kN
z
z
5 cm
20 cm
y
6 cm
25 cm
y
Resolução:
1. Características da seção:
A = b × h = 250 × 200 = 5 × 10 4 mm 2
y
5 cm
b3 × h 2003 × 250
Iy =
=
=
12
12
166,7 ×106 mm 4
z
20 cm
b × h3 200 × 2503
Iz =
=
=
12
12
260,4 ×106 mm 4
6 cm
25 cm
2. Esforços solicitantes em todas as seções:
N = −950 kN = −950 × 103 N
M z = − F × ez
M z = −950 × 103 × 60 = −57 × 106 Nmm
M y = F × ey
M y = +950 × 103 × 50 = +47,5 × 106 Nmm
3. Equação da Tensão Normal (σx):
My
N Mz
σx = +
y−
z
Iy
A Iz
− 950 × 103
57 × 106
47,5 × 106
σx =
y−
z
−
4
6
6
5 × 10
260,4 × 10
166,7 × 10
⇒ σ x = −19 − 0,219 y − 0,285 z
Analisando a equação da tensão normal, observa-se
que σx depende de y e de z.
y = distância do ponto onde se quer calcular a tensão
até o eixo z que passa pelo centróide da seção
z = distância do ponto onde se quer calcular a tensão
até o eixo y que passa pelo centróide da seção
4. Cálculo da Tensão Normal (σx):
σ x = −19 − 0,219 × (+ 125 ) − 0,285(+ 100 )
100mm
• Para y = +125mm e
z = +100mm, tem-se:
σ x = −74,88MPa
σ x = −19 − 0,219 × (+ 125 ) − 0,285(− 100 )
σ x = −17,88MPa
y
100mm
• Para y = +125mm e
z = -100mm, tem-se:
z
125mm
125mm
• Para y = -125mm e
z = +100mm, tem-se:
σ x = −20,13MPa
σ x = −19 − 0,219 × (− 125 ) − 0,285(− 100 )
σ x = +36,88MPa
z
y
100mm
• Para y = -125mm e
z = -100mm, tem-se:
100mm
σ x = −19 − 0,219 × (− 125 ) − 0,285(+ 100 )
125mm
125mm
5. Posição da Linha Neutra:
Como a linha neutra é o lugar geométrico dos pontos
onde σx= 0, tem-se que:
σ x = −19 − 0,219 y − 0,285 z = 0
∴ y = 0 ⇒ z = −66,7 mm
∴ z = 0 ⇒ y = −86,8mm
6. Diagrama de Tensão Normal (σx):
-74,88MPa
-20,13MPa
L.N.
-17,88MPa
+36,88MPa
z
y
+36,88MPa
-74,88MPa
L.N.