8. Flexão, tensão normal e raio de curvatura
Propaganda
8. Flexão, tensão normal e raio de curvatura Terminologia: Relativamente à posição da carga M Flexão recta ou plana: o plano do momento contém um dos eixos centrais principais de inércia Flexão desviada: não é recta M Relativamente aos outros esforços Flexão pura: não está acompanhada pelo esforço de corte, o momento flector é constante e único esforço interno Flexão simples: não está sobreposta com o esforço normal Flexão composta: está sobreposta com o esforço normal Estruturas onde o único esforço interno é o momento flector: “sistemas encastrado-livre” sujeitos à carga do momento (flector) concentrado 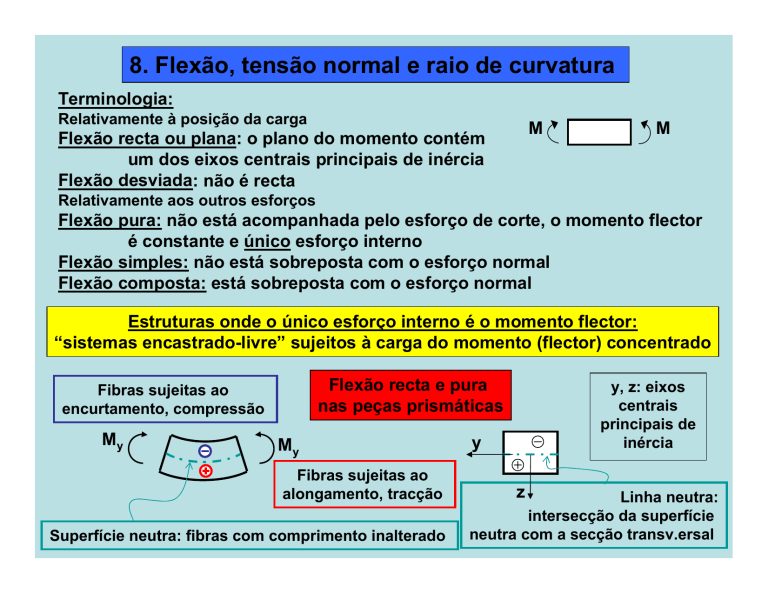Flexão recta e pura nas peças prismáticas Fibras sujeitas ao encurtamento, compressão My My Fibras sujeitas ao alongamento, tracção Superfície neutra: fibras com comprimento inalterado y, z: eixos centrais principais de inércia y z Linha neutra: intersecção da superfície neutra com a secção transv.ersal comprimento original: dx comprimento novo: (R+z)dθ Linha do ponto P εx = dθ R σx My My P(z) ( R + z )dθ − dx =E dx (R + z )dθ − dx dx devido a Usando as equações de equivalência N = ∫ σ x dA = ∫ E A A (R + z )dθ − dxdA = 0 (z variável) dx ∫ ((R + z )dθ − dx )dA = (Rdθ − dx )A + dθ ∫ zdA = (Rdθ − dx )A = 0 A σ y = σz = 0 ⇒K= A ⎛ dx ⎞ ⎜ + z ⎟dθ − dx (R + z )dθ − dx = ⎝ dθ ⎠ z εx = = dx dx R yz M z = − ∫ σ x ydA = − ∫ E dA = 0 R A A eixos principais eixos centrais z σx = E R 1 dθ = R dx Linha neutra ≡ y Iy z2 M y = ∫ σ x zdA = ∫ E dA = E R R A A Além disso foi provada a distribuição linear da tensão normal Fórmula de Euler-Bernoulli My σx = σ = z Iy My 1 K xz = = R xz EI y My εx = z EI y σx M compressão linha neutra tracção σx = ± M I linha neutra d linha neutra d: distância do ponto em causa da linha neutra Rigidez em flexão: EI assegura igual curvatura para o mesmo carregamento (Módulo de) Resistência em flexão: cima y W Iy = cima d max σ cima x ,max = assegura igual tensão normal máxima W para o mesmo carregamento My cima y W baixo y W = Iy d baixo max σ baixo x ,max = My Wybaixo É preciso distinguir o máximo em tracção e em compressão Flexão desviada e composta Princípio de sobreposição N My M σ= + z− z y A Iy Iz Rigidez / Deformação Carga Resistência / Tensão máxima Normal EA εx = du N = dx EA Flexão EI K= dθ M = dx EI W= GIT θ= dβ T = dx GIp WT = Torção W=A σ máx = x N W I σ máx = x M W τmáx xs = T WT d máx IT R máx
