Probabilidade e Distribuicoes

Probabilidades:
Probabilidade
e
Distribuicoes
A probabilidade de um evento A mede de alguma maneira, quão
verossímel é a ocorrência do evento A.
Probabilidade Clá
Clássica
É aplicada quando o espaço amostral Ω é finito e os eventos
elementares são equiprováveis; isto é, eles têm a mesma probabilidade
de ocorrer. Seja A um evento qualquer do espaço amostral Ω. Define-se
a probabilidade de A como a razão entre o número de resultados
favoráveis ao evento e o número total de resultados possíveis, onde
todos os resultados possíveis têm a mesma chance de ocorrer.
P ( A)
Prof. Tania Guillén de Torres
E-mail: [email protected]
=
número de resultados favoráveis à ocorrência
número de resultados possíveis
de A
Essa interpretação é difícil de ser utilizada como regra geral, até pela
dificuldade de garantir que os resultados tenham a mesma chance de
ocorrência.
Probabilidades:
Probabilidade Freqüentista
Em situações onde os elementos do espaço amostral não são
igualmente prováveis, a probabilidade de ocorrer o evento A
pode ser calculada através da noção de freqüência relativa.
Se um experimento E for repetido um grande número de
vezes, n, e se algum evento A ocorre nA vezes, a freqüência
relativa do evento A é definida por:
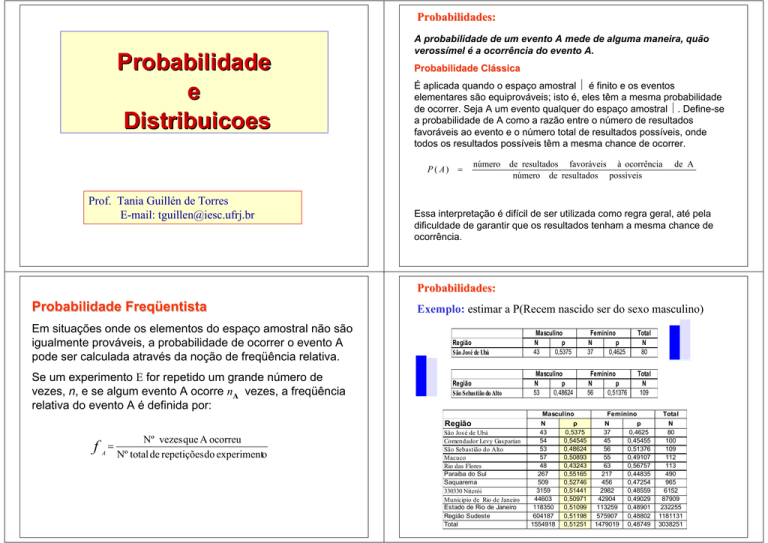
Exemplo: estimar a P(Recem nascido ser do sexo masculino)
Região
São José de Ubá
Masculino
N
p
43
0,5375
Feminino
N
p
37
0,4625
Total
N
80
Região
São Sebastião do Alto
Masculino
N
p
53
0,48624
Feminino
N
p
56
0,51376
Total
N
109
Masculino
Região
f
A
=
Nº vezes que A ocorreu
Nº total de repetições do experimento
São José de Ubá
Comendador Levy Gasparian
São Sebastião do Alto
Macuco
Rio das Flores
Paraíba do Sul
Saquarema
330330 Niterói
Municipio de Rio de Janeiro
Estado de Rio de Janeiro
Região Sudeste
Total
N
43
54
53
57
48
267
509
3159
44603
118350
604187
1554918
p
0,5375
0,54545
0,48624
0,50893
0,43243
0,55165
0,52746
0,51441
0,50971
0,51099
0,51198
0,51251
Feminino
N
37
45
56
55
63
217
456
2982
42904
113259
575907
1479019
p
0,4625
0,45455
0,51376
0,49107
0,56757
0,44835
0,47254
0,48559
0,49029
0,48901
0,48802
0,48749
Total
N
80
100
109
112
113
490
965
6152
87909
232255
1181131
3038251
n = 800
1
n = 80
0,55
.8
.2
0
0
ERJ - Frequencia relativa do recem nascido sexo masculino
por número de nascidos vivos.
.2
.4
Density
.4
Esta característica é conhecida como regularidade estatística.
Density
.6
.6
À medida que o número de repetições do experimento aumenta,
a freqüência relativa de ocorrência de algum evento A tende a
se estabilizar e será igual à probabilidade de ocorrência de A.
Distribuição do Peso ao nascer para diferentes tamanhos de amostra
.8
Probabilidades: P(Recem nascido ser do sexo masculino)
1
2
3
Peso em Kgr
4
1
5
2
3
P eso em Kg r
4
5
1
0,54
.8
0,52
0,51
n = 80 000
.4
0,50
Density
.6
(%)
0,53
50000
100000
150000
200000
250000
0
0
.2
0,49
0
Probabilidade Subjetiva
Esta interpretação expressa na probabilidade a confiança que
determinado indivíduo tem acerca da verdade de uma proposição,
incorporando o conhecimento que ele dispõe sobre o evento.
Exemplo: Pela sua experiência, um cirurgião pode tranqüilizar os
familiares de um paciente que será submetido a uma cirurgia delicada,
com base na sua confiança no sucesso.
2
4
Peso em Kgr
6
8
Exemplo: Foi realizado um estudo prospectivo de um ano, de 477 pacientes tratados por
acidentes com corpos estranhos (CE) otorrinolaringológicos pelo serviço de ORL / EPO–
HMSA / RJ, observando-se a seguinte distribuição: Qual a probabilidade de que um
paciente escolhido ao acaso seja tratado por um acidente com CE auricular (CE-A),
sabendo que ele é do sexo masculino? E se for do sexo feminino?
Tipo de Corpo
Extranho
Sexo
Masculino
Femenino
Total
Nasal
130
99
229
Auricular
71
75
146
Faríngeo
47
55
102
Total
248
229
477
Probabilidade Condicional
A probabilidade de um evento A ocorrer, dado que se sabe que um
outro evento B ocorreu, é chamada de probabilidade condicional do
evento A dado B. Ela e denotada por
P( A | B) =
P( A ∩ B)
P( B)
Exemplo: Foi realizado um estudo prospectivo de um ano, de 477 pacientes tratados por
acidentes com corpos estranhos (CE) otorrinolaringológicos pelo serviço de ORL / EPO–
HMSA / RJ, observando-se a seguinte distribuição: Qual a probabilidade de que um
paciente escolhido ao acaso seja tratado por um acidente com CE auricular (A), sabendo
que ele é do sexo masculino (M)? E se for do sexo feminino?
Tipo de Corpo
Extranho
Sexo
Masculino
Femenino
Total
Nasal
130
99
229
Auricular
71
75
146
Faríngeo
47
55
102
Total
248
229
477
=
P ( ( A) ∩ M )
P(M )
71 / 477
= 0.29
248 / 477
ESTUDOS DE COORTE
Probabilidade Condicional
A probabilidade de um evento A ocorrer, dado que se sabe que um
outro evento B ocorreu, é chamada de probabilidade condicional do
evento A dado B. Ela e denotada por
P( A | B) =
P( A | M ) =
P( A ∩ B)
P( B)
Seleciona expostos e não expostos e compara a ocorrência do
desfecho depois de um período de seguimento
Presente
Futuro
Observe que a partir desta definição a probabilidade da interseção
A ∩ B pode ser expressa como:
Expostos
P( A ∩ M ) = P( A | M ) × P( M )
ou
P( A ∩ M ) = P ( M | A) × P ( A)
Doentes?
Não Expostos
Risco de doença
R
Doença
=
número de Doentes no ano
número de vivos no inicio do ano
Aplicações do Conceito de Probabilidades Condicionais
Estudo de Coorte
R = Risco =
I
N
RMorte =
ERJ – Razão de Probabilidade de Morte por todas as
causas, por sexo segundo faixa etária - 2003
número de mortes no ano
número de vivos no inicio do ano
Idade
Menor 1 ano
1 a 4 anos
5 a 9 anos
10 a 14 anos
15 a 19 anos
20 a 29 anos
30 a 39 anos
40 a 49 anos
50 a 59 anos
60 a 69 anos
70 a 79 anos
80 anos e mais
ERJ – Probabilidade de Morte por todas as causas segundo o sexo 2003
Sexo
Masc
Fem
Total
Óbitos
65934
50310
116318
Pop_Resident Probabilidade de Morte Razao de Prob
7136931
0.009238425
1.421702489
7742213
0.006498142
14879144
0.00781752
65934
R mortemasculino = 7136931 = 0,0092
R morte fe min ino
=
50310
= 0,0065
7742213
Razão de Riscos:
RR morte:masc / fem =
R morte
Rmorte
masculino
fe min ino
=
0,0092
= 1,42
0,0065
ESTUDOS CASO-CONTROLE
Seleciona casos com doença e controles sem doença e
compara a freqüência da exposição
Passado
Expostos
Presente
Casos
Probabilidade
Masculino
0.018031028
0.000727395
0.000361247
0.000485368
0.002821425
0.004154793
0.003988123
0.007289989
0.014945402
0.029601933
0.063303795
0.140738117
Feminino
0.014716583
0.000613201
0.000234514
0.000256744
0.00053035
0.000826367
0.001491504
0.003555948
0.007884982
0.016255489
0.039493554
0.116693236
RR
1.225218341
1.186226949
1.540407538
1.890472989
5.319928537
5.027782956
2.673893031
2.050083484
1.895426295
1.821042227
1.602889291
1.206052052
Aplicações do Conceito de Probabilidades
Estudos Caso-Controle
Odds =
Chance
odds =
OR -Razão de
Chances
OR
P( D +)
0,009
=
= 0,0091
1 − P ( D + ) 1 − 0,009
odds
=
odds
P ( D + | e+)
0 , 009
e + = 1 − P ( D + | e + ) = 1 − 0 , 009 = 1, 4217
0 , 006
P ( D + | e −)
e−
1 − 0 , 006
1 − P ( D + | e−)
ERJ – Probabilidade de Morte por todas as causas - 2003
Não
Expostos
Controles
Sexo
Masc
Fem
Total
Óbitos
65934
50310
116318
Pop_Resident Probabilidade de Morte
7136931
0.009238425
7742213
0.006498142
14879144
0.00781752
OR
1.421702489
Aplicações do Conceito de Probabilidades
Estudos Caso-Controle
ERJ – Probabilidade de Fumar nos grupos com e sem Ca.
Laringe
Aplicações do Conceito de Probabilidades
Estudos Caso-Controle
ERJ – Probabilidade de Ca. Laringe
nos grupos fuma e não fuma
Fumo (F)
Não (F-)
Cancer de Laringe n- Ca
p
Não (CA-)
330
0,9167
Sim (Ca+)
180
0,50
Total
510
0,7083
Odds de Fumo
odds F + =
OR
F+
=
odds
F + Ca +
odds
F + Ca −
Sim (F+)
n
p
30
0,0833
180
0,50
210
1.00
Fumo
Total
n
360
360
720
P(F +)
P(F +)
=
1 − P ( F + ) P ( F −)
P ( F + | Ca
P ( F − | Ca
=
P ( F + | Ca
P ( F − | Ca
Não
%
0,50
0,50
1,00
+)
0 ,5000
)
+ = 0 , 5000 = 11.0048
0 , 0833
−)
0 ,9167
−)
INQUÉRITO OU ESTUDO SECCIONAL
Estimam a prevalência da doença na população total,
ou em estratos dessa população.
Cancer de Laringe n
Não
330
Sim
180
Total
510
Sim
%
64,71
35,29
100,00
n
30
180
210
Total
%
14,29
85,71
100,00
Odds de Câncer de Laringe: odds Ca + =
Razão de Odds de Câncer de
Laringe:
P ( Ca
odds Ca + / F + P ( Ca
=
OR Ca + =
odds Ca + / F − P ( Ca
P ( Ca
n
360
360
720
%
50
50
100
P (Ca + )
1 − P (Ca + )
| F +)
0 ,8571
− | F + ) = 0 ,1429 = 11.0048
0 , 3529
+ | F −)
0 , 6471
− | F −)
+
Disfonia em professores do ensino municipal:
prevalência e fatores de risco
A disfonia é um sintoma muito freqüente em professores,
profissionais para os quais a voz é elemento indispensável.
Objetivos:
Observar a prevalência deste sintoma em professores
de pré-escola e da escola primária.
Casuística e Método:
•
Estudo transversal consistindo de questionários respondidos
por 451 professores (pré-escola e quatro primeiras séries do
ensino fundamental) de 66 escolas municipais de Mogi das
Cruzes
Exemplo de Dependência Estatística:
Disfonia em professores do ensino municipal:
prevalência e fatores de risco
Resultados:
80,7% dos professores referiram algum grau de disfonia.
Não observamos relação entre idade, tempo de profissão e
As probabilidades de morte por câncer de pulmão
podem ser melhor preditas, se são conhecidos os hábitos de
fumo dos indivíduos. Suponha que as probabilidades são de
0.015 para os fumantes e 0.005 para os não fumantes, então
essas probabilidades são condicionais e dependentes ao
tabagismo (exposição).
classe atendida e freqüência referida de disfonia.
Disfonia
Não
Cancer de Laringe n
Pré-escola
40
EnsinoFund.
42
Total
82
P = Prevalência da doença
RP = Razão de Prevalência
Sim
p
0,20
0,25
0,19
n
228
129
357
RPDisf =
n
268
171
439
p
0,61
0,39
1,00
Morte Sobrevida
0.006
0.394
E - (não)
Total
E - (não)
Total
Morte Sobrevida
0.006
0.394
Total
0.4
0.003
0.597
0.6
0.009
0.991
1
PDisfPré−escola 0,80
=
=1,07
0
,
75
PDisfEnsinoFund
Independência Estatística:
Exemplo de Dependência Estatística:
Fuma
E + (sim)
Fuma
E + (sim)
Total
p
0,80
0,75
0,81
Total
0.4
0.003
0.597
0.6
0.009
0.991
1
No exemplo, a probabilidade de morte difere de acordo com a
exposição ou não ao fumo.
P(M|E+) = 0,015 ≠ P(M|E-) = 0,005)
logo os eventos “Morte” e “Fumo” são eventos dependentes.
Se a probabilidade de morte é a mesma se o
indivíduo está exposto ou não a algum fator, diz-se que a
morte e o fator de exposição são estatisticamente
independentes.
Dois eventos são independentes se a ocorrência
ou não ocorrência de um deles não afeta a probabilidade
de ocorrência ou não ocorrência do outro.
Exemplo: Suponha agora o estudo de câncer (M = morte, S = sobrevida)
e cor dos cabelos (L = louro, NL = não louro).
Obs: Câncer e cor natural dos
cabelos seriam eventos
independentes, pois
P(M|L) = P(M|NL) = 0,009
Teorema de Bayes e Testes Diagnósticos
Uma aplicação muito útil e freqüente envolvendo probabilidade condicional é o
Teorema de Bayes. Para entendê-lo melhor, primeiro será feita uma aplicação prática
para então formalizá-lo.
A pergunta é: Dado que o teste teve um resultado positivo, qual a
probabilidade de estar doente efetivamente? Chama-se esta probabilidade
de valor preditivo positivo (VPP).
VPP = Valor preditivo positivo =
Pela definição de probabilidade condicional,
Suponha um teste com os valores de sensibilidade e especificidade conhecidos.
Sensibilidade = S = P (Τ
Τ+|D+) Probabilidade do teste ser + no grupo de D+
Especificidade = E = P (Τ
Τ− | D −) Probabilidade do teste ser - no grupo de DPrevalência = p = P (D+)
(probabilidade de doença ou probabilidade a priori)
P (D+|T+)
P (D+|T+) = P (D+ ∩ T+) / P (T+).
Probabilidade do teste ser positivo,
P(T+) = P(T+ ∩ D+) + P(T+ ∩ D−) = P(T+|D+)×
×P(D+) + P(T+|D−)×
×P(D−)
=
p × S + (1 – p) × (1 – E)
Aplicando a lei da multiplicação no numerador da relação acima,
P (D+ ∩ T+) = P (T+|D+) × P (D+) = p × S
= Sensibilidade x Prevalência da doença.
Agora, com todos os termos conhecidos, pode-se reescrever
VPP = P ( D+ | T+ ) =
P ( D+ ∩ T+ )
P (T+ | D+ ) P ( D+ )
ou
=
P (T+ )
P (T+ | D+ ) P ( D+ ) + P (T+ | D− ) P ( D− )
VPP = P ( D+ | T+ ) =
De forma análoga podemos obter uma expressão para o valor de predição
negativo
VPN = P ( D − | T − ) =
(1 − p ) × E
(1 − p ) × E + p × (1 − S )
S. p
S . p + (1 − E ).(1 − p )
Se a prevalência da Aids fosse de 15/100000, qual seria o
valor de predição positiva do teste? E o valor de predição
negativa do teste?
Decisões Incorretas:
Probabilidade de Falso Positivo: PFP = P(D - | T+) = 1 - P(D+ | T+) = 1 – VPP
Probabilidade de Falso Negativo: PFN = P(D+ | T-) = 1 - P(D - | T-) = 1 – VPN
Exemplo: Teste ELISA para detecçã
o do HIV (Ref. F. Soares)
detecção
Durante o mês de julho de 1985, a imprensa, através de editoriais, tratou
freqüentemente do assunto Aids. Um dos pontos em questão era o teste que
detecta a presença do vírus HIV. A versão do laboratório Abbott do teste
produziu 37 resultados positivos em 17420 amostras de sangue de pessoas
sadias; e 123 positivos em 129 pacientes, comprovadamente, com Aids.
Resultado do Teste
Calcule a sensibilidade e a especificidade do teste.
S = P(T+|D+) = 123/129 = 0,9535,
e
Τ− | D −) = (17420-37)/ 17420 = 17383/17420 = 0,9979
E = P (Τ
T+
T-
Doença
D+
DTotal
0,000143025 0,000006975 0,00224271
0,002099685 0,997750315 0,99775729
Exemplo: Teste ELISA para detecçã
o do HIV
detecção
Resultado do Teste
T+
T-
Doença
D+
DTotal
0,000143025 0,000006975 0,00224271
0,002099685 0,997750315 0,99775729
P(T+) = P(T+ ∩ D+) + P(T+ ∩ D-) = 0,000143025+ 0,002099685
= 0,00224271
VPP = P(D+ | T+) =
P (T + ∩ D + ) 0,000143025
= 0,06377
=
0,00224271
P (T + )
cont...
Valores de Predição (VPP E VPN) e proporção de falsos resultados (PFP e PFN) e proporção
de falsos resultados (PFP e PFN) do teste Elisa para detecção do HIV, versão ABBOTT, para
diferentes possíveis valores da prevalência (Ref. Fco. Soares, 1995).
Prevalência
1/100000
1/10000
1/1000
1/500
1/200
1/100
1/50
VPP(%)
0,47
4,54
32,21
48,77
70,47
82,75
90,65
VPN(%)
100,00
100,00
99,99
99,99
99,99
99,99
99,89
PFP(%)
99,53
95,46
67,79
51,23
29,53
17,25
9,35
PFN(%)
0,00
0,00
0,01
0,01
0,01
0,01
0,11
HIV/AIDS: Doença de prevalência pequena
Valor de Predição Positiva é pequena
Valor de Predição Negativa é alto
P(T-) = P(T- ∩ D+) + P(T- ∩ D -) = 0,000006975+ 0,997750315= 0,99775729
VPN = P(D- | T-) =
P (T − ∩ D − ) 0,997750315
= 0,99999
=
P (T − )
0,99775729
Variáveis Aleatórias e Distribuições de Probabilidades
A partir da realização de um experimento, pode-se estar interessado não
apenas no resultado observado, como também em alguma função do
espaço amostral em questão. Essas funções definidas no espaço amostral
são chamadas de variáveis aleatórias.
Exemplo: Num estudo sobre obesidade em adultos, um experimento
consiste em observar o peso e a altura dos indivíduos. Se I for o Índice de
Massa Corporal ( ), então I é uma variável aleatória que pode assumir
qualquer valor real maior que zero.
Como os valores de uma variável aleatória são determinados pelo
resultado de um experimento, pode-se associar probabilidades aos valores
possíveis de um variável aleatória.
As variáveis aleatórias podem ser classificadas como discretas ou
contí
contínuas.
Uso do teste em larga escala poderia resultar em testes falsos positivos
Resultado positivo deve ser reconfirmado através de teste baseado em tecnologia diferente do
ELISA.
É desejado prever, de alguma forma, o valor que a variável aleatória X irá
assumir (ou conhecer o comportamento da distribuição), embora essa
predição envolva um grau de incerteza. Diante disso, relaciona-se os
valores de uma variável aleatória e a probabilidade de suas ocorrências.
Duas funções são utilizadas para este fim: a função de densidade de
probabilidade e a função de distribuição acumulada.
No caso de variáveis aleatórias discretas, a função de densidade chama-se
simplesmente distribuição de probabilidades e mede a probabilidade de que a v. a.
X assuma um valor específico x ( P(X = x) ).
Suponha X = número de crianças por
família em uma amostra de 50 famílias. A
tabela a seguir especifica todos os valores
possíveis para X e as respectivas
probabilidade de ocorrência e função de
distribuição acumulada, estimadas a partir
das freqüências relativas na amostra
observada.
P(X = x)
0
Freqüência
observada
3
0,06
0,06
1
10
0,20
0,26
2
18
0,36
0,62
3
4
5
6
8
8
5
2
3
1
50
0,16
0,10
0,04
0,06
0,02
1,00
0,78
0,88
0,92
0,98
1,00
X
P(X <= x)
Distribuiçã
o Binomial
Distribuição
Distribuição de Probabilidades do número de sucessos quando n = 3
Uma das distribuições de probabilidade mais largamente aplicadas é a
distribuição binomial. Ela tem por base o ensaio de Bernoulli, que é um
experimento que apresenta apenas dois resultados possíveis,
mutuamente excludentes, tais como morrer ou sobreviver, masculino ou
feminino, sucesso ou fracasso.
Suponha que determinada cirurgia apresente 80% de probabilidade de
sucesso. A variável de interesse X é número de sucessos. Então, para um
paciente, tem-se:
w
X
P (X=x )
FFF
FFS ou FSF ou SFF
0
1
1. 0,80 . 0,23
3. 0,81 . 0,22
FSS ou SFS ou SSF
2
3. 0,82 . 0,21
SSS
3
1. 0,83 . 0,20
De forma geral, assumindo que:
1. tem-se n ensaios de Bernoulli
⇒
Ω={F,S}
w
F
S
P (X=x )
q = 1-p = 0,2
p = 0,8
X
0
1
2. os ensaios são independentes
3. a probabilidade de sucesso é igual a p em qualquer ensaio,
a distribuição Binomial estabelece que:
⇒
Ω = { FF, FS, SF, SS }
w
P (X=x )
X
FF
0
P(F∩F) = P(F) P(F) = (1-p)2 = 0.22
FS ou SF
1
P(F∩S) + P(S∩F) = 2 p (1-p) = 2 . 0.81 .0.21
SS
2
P(S∩S) = p2 = 0.82
n
P( X = x) =   p x (1 − p) n − x
 x
Dados os parâmetros da distribuição binomial (n e p), a média e a
variância de uma variável aleatória com essa distribuição são dadas por
np e np(1-p), respectivamente.
Média (X) = µ = n p
Variância (X) = σ2 = n p (1-p)
Exemplo: Suponha que 30% de uma população é imune a uma certa
doença. Qual a probabilidade de, num grupo de 5 pessoas desta
população, encontrarmos: 3 imunes?
a)
Seja X = número de pessoas imunes a doença
n = 5 pessoas observadas
p = 0,30 é a probabilidade de uma pessoa ser imune a doença
evento de interesse: [x = 3], logo
n
P(X = x | p = 0.3)
0.40
 5
P( X = 3) =   0,33 (1 − 0,3) 5 − 3 = 10 × (0,3)3 (0,7 )2 = 0,1323
 3
0.35
0.30
0.25
0.20
0.15
0.10
0.05
0.00
0
1
2
3
4
5
P(X=3) quando: n=5 e p = 0,30
Distribuição de Poisson
Distribuição de Probabilidade Binomial
quando: n = 5 e p = 0,3
Outra distribuição utilizada para modelar variáveis do tipo quantitativo
discreta é a distribuição de Poisson,
Empregada para modelar a ocorrência de eventos raros (eventos
com probabilidade de ocorrência muito pequena).
P(X = x | p = 0.3)
x P( X = x | p = 0.3 )
0
0.16807
1
0.36015
2
0.30870
3
0.13230
4
0.02835
5
0.00243
0.40
0.35
0.30
0.25
0.20
0.15
0.10
0.05
0.00
0
1
2
3
4
5
Exemplos:
1. Número de chegadas a um pronto-socorro durante a madrugada
b) Qual seria o valor com maior probabilidade de acontecer?
2. Número de pessoas com leucemia numa cidade
c) Qual a Probabilidade do número de imunes variar entre 3 e 5 inclusive?
3. Número de acidentes de carro na Ponte Rio-Niterói por dia
4. Número de metamielócitos no sangue de pessoas sadias
P( 3 ≤ X ≤ 5) = P(X = 3) + P(X = 4) + P(X = 5)
= 0,13230 + 0,02835 + 0,00243 = 0,16308
Distribuição de Poisson
A distribuição de Poisson geralmente está associada a um processo
aleatório, que objetiva estudar o número de eventos de interesse e o
tempo entre a ocorrência de dois eventos seguidos.
Este processo é chamado de Processo de Poisson e apresenta as
seguintes características:
O número de eventos que ocorrem num determinado intervalo de
tempo (ou espaço) é independente do número de eventos que
ocorrem num outro intervalo de tempo (ou espaço) disjunto do
primeiro.
Os eventos de interesse (falhas) ocorrem com alguma taxa média
de ocorrência λ, que é constante para todo intervalo de tempo (ou
espaço).
Quanto menor for o intervalo de tempo considerado, menor será a
probabilidade de que aconteça mais de um evento de interesse
nesse intervalo.
Distribuição de Poisson
Proporciona as probabilidades do número de "falhas" que
acontecem num determinado período de tempo ou espaço (ou
volume de matéria).
Para X = Número de Falhas
A probabilidade de X assumir um valor igual a k é dada por:
P( X = k ) = λ e
k
−λ
k!
onde :
,
k = 0,1,2,L
X = número de eventos
λ = taxa média do processo
k = 0,1,2, ...
e = 2.7182818.. (número de Euler)
Na distribuição de Poisson, a média e a variância são iguais a α.
= µ
Média (X)
Um hospital recebe em média quatro chamadas de urgência por dia.
= λ
Desejando melhor equipa-lo para suas funções, necessita-se
Variância (X) = σ2 = λ
conhecer qual a probabilidade de que o hospital receba:
= √λ
Desvio Padrão = σ
Exemplo:
a) Oito chamadas?
λ=4
λ=1
X = número de chamadas de urgência num dia
0.25
0.40
0.20
0.30
0.15
0.20
0.10
0.10
0.05
0.00
0
1
2
3
4
5
6
7
8
0.00
9
0
1 2
3
4 5
6
7 8
8 −4
9 10 11 12 13 14 15 16 17
P ( X = 8) = 4 e
8!
λ = 10
0.14
= 0.03
0.12
0.10
0.08
0.06
0.04
0.02
0.00
0
b)
1
2
3
4
5
6
7
8
9
10
11 12 13
14
15
16
17
18
19 20 21 22 23 24 25
Três ou menos chamadas num dia?
Distribuiçã
o de Poisson como Aproximaçã
o da Distribuiçã
o Binomial
Distribuição
Aproximação
Distribuição
P(X ≤ 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)
Quando:
= 0,018 + 0,073 + 0,147 + 0,195 = 0,433
o número de realizações de um experimento binomial (n) é grande e
a probabilidade de sucesso (p) é muito pequena de modo que np ≤ 7,
a distribuição binomial pode ser aproximada pela distribuição de
Poisson com
α=n×p
Distribuiçã
o de Poisson como Aproximaçã
o da Distribuiçã
o Binomial
Distribuição
Aproximação
Distribuição
Distribuição Normal ou Gaussiana
Exemplo: A probabilidade de uma pessoa sofrer intoxicação alimentar na
Tem sua origem associada ao eminente matemático alemão Gauss que
ao utilizá-la na construção da teoria dos erros, mostrou sua importância,
porém ela foi primeiramente estudada por Abraham de Moivre.
lanchonete de um parque de diversões é 0,001. Qual a probabilidade de
que em 2.000 pessoas que passam o dia no parque, duas sofram de
intoxicação alimentar?
α = n p = 2000 x 0,001 = 2
A distribuição Normal (ou Gaussiana) também é associada às medidas
biológicas e às medidas de produtos fabricados em série.
A distribuição Normal de uma variável aleatória contínua tem a seguinte
função de densidade:
P(X = 2) = 0,2707
x
0.0000
1.0000
2.0000
3.0000
4.0000
5.0000
6.0000
7.0000
8.0000
9.0000
f ( x) =
P(X=k)
0.1353
0.2707
0.2707
0.1804
0.0902
0.0361
0.0120
0.0034
0.0009
0.0002
1
2
1
e− 2 2 (x−µ )
σ
σ 2π
onde µ (média) e σ (desvio padrão) são os parâmetros da distribuição.
Algumas características da distribuição Normal:
1. A variável aleatória pode assumir qualquer valor (- ∞ < x < + ∞).
2.
Α expressão: X ~ N ( µ , σ ) denota que a variável aleatória X tem
distribuição Gaussiana ou Normal com média µ e desvio-padrão σ.
2
3. Na distribuição Normal a Média, Mediana e a Moda são iguais a µ .
4. A área total sob a curva e acima do eixo horizontal é igual a 1.
Distribuições Normais com o mesmo desvio-padrão e diferentes médias
(µ1 ≠ µ2 ), possuem a mesma forma mas diferem quanto a localização.
Isto é, quanto maior o valor da média mais à direita estará a curva.
Observe na figura que a distribuição em vermelho apresenta maior valor
para a média.
Área = 1
Para um mesmo valor de média e valores diferentes de desvio-padrão, a
distribuição com desvio-padrão de maior valor é mais “achatada”,
A área sob a curva normal
acusando maior variabilidade em torno da média. Aquela que tem menor
desvio-padrão, apresenta um pico e tem menor dispersão em torno da
média.
µ±1σ
68,26%
µ ± 1,96 σ 95,00%
µ ± 2,58 σ 99,00%
Distribuiçã
o Normal Padrã
Distribuição
Padrão
Distribuiçã
o Normal Padrã
Distribuição
Padrão
Uma distribuição Normal com média µ = 0 e desvio-padrão σ = 1, é
Z é uma variável continua logo P(Z = a) = 0, para qualquer
chamada de distribuição Normal padrão.
valor de a.
Para o caso: média µ = 0 e desvio-padrão σ = 1 foram
calculadas probabilidades da variável aleatória assumir
valores menores ou iguais a z0
i.e. P(Z ≤ z0),
disponibilizadas em tabelas ou em pacotes computacionais.
Uma variável aleatória com distribuição Normal padrão é usualmente
identificada pela letra Z, e representada por:
Z~N(0,1)
P(Z ≤ - 2,58) = 0,0049
P(Z ≤ - 0,74) = 0,2296
P(Z ≤ 2,00) = 0,9772
P(Z ≤ 2,58) = 0,9951
Calculo de Probabilidades do tipo: P(a < Z ≤ b)
Calculo de Probabilidades do tipo P(Z > z0),
P(Z > 2)
P(-1,96 < Z ≤ 1,96)
=
P(Z > 2)
-
=
1
P(Z ≤ 2)
= 1 - 0,9772 = 0.0228
=
1 -
P(Z > -1) = 1 - P(Z ≤ -1) = 1 - 0,1587 = 0.8413
-
=
P(-1,96 < Z ≤ 1,96)
=
P(Z ≤ 1,96)
-
=
0,9750
-
=
0,95
P(Z ≤ - 1,96)
0.02499
Calculo de Probabilidades do tipo: P(a < Z ≤ b)
Padronização:
Quando uma variável aleatória tem distribuição normal
P(-2,58 < Z ≤ 2,58)
-
=
com média µ ≠ 0 e σ ≠ 1
deve-se padronizar a variável através da seguinte transformação:
Z
=
x−µ
σ
A variável Z tem agora distribuição normal padrão (µ = 0 e σ = 1)
P(-2,58 < Z ≤ 2,58)
=
P(Z ≤ 2,58)
- P(Z ≤ - 2,58)
=
0,0.995
-
=
0,990
0.005
Escore padronizado
x i − µ , i = 1,2,..., n
=
zi
σ
Diferentemente do Coeficiente de Variação, o escore padronizado, é útil para
Escore padronizado
Exemplo:
Os escores padronizados são amplamente utilizados em teste de aptidão física.
Mathews (1980) compara testes de aptidão física e conhecimento desportivo.
comparação dos resultados indivíduais.
Os escores padronizados são muito úteis na comparação da posição relativa da
medida de um indivíduo dentro do grupo ao qual pertence, o que justifica sua
grande aplicação como medida de avaliação de desempenho.
Tabela 10: Resultados obtidos por duas alunas do curso secundário, média e desvio
padrão da turma em teste de aptidão física e conhecimento desportivo.
Teste
µ
σ
Maria
Joana
Maria
Joana
abdominais em 2 min
30
6
42
38
2,00
1,33
salto em extensão (cm)
155
23
102
173
-2.33
0,78
suspensão braços flexionados
(seg)
50
8
38
71
-1.50
2,63
1829
274
2149
1554
1,17
-1,00
75
12
97
70
1,83
-0,42
correr/andar em 12 min (m)
conhecimento desportivo
Fonte: http://leg.ufpr.br/~silvia/CE055/node27.html
x
Fonte: http://leg.ufpr.br/~silvia/CE055/node27.html
z
Escore padronizado
Exemplo: O conteúdo de glicose no sangue em pessoas adultas pode ser
(corrida/caminhada) está acima da média mas não é notável e ela tem um
considerado normalmente distribuído com média 100mh/100ml e desvio
padrão 10mg/100ml. Suponha que 500 indivíduos da população são
escolhidos ao acaso. Se os indivíduos com um conteúdo de glicose igual ou
maior que 120mg/100ml são considerados diabéticos, qual o número
esperado de diabéticos entre os 500 indivíduos escolhidos?
conhecimento desportivo bastante bom comparado com o grupo.
Seja X = conteúdo de glicose com distribuição X ~ N ( µ = 100 , σ = 10 )
Maria apresentou um desempenho muito acima da média em força
abdominal (dois desvios padrão acima da média); sua capacidade aeróbica
No salto de extensão e na suspensão com flexão do braço sobre
P( X > 120 ) = P (
X − 100 120 − 100
>
10
10
) = P(Z > 2 ) = 1 - P( Z ≤ 2 ) =
antebraço, Maria obteve escores abaixo das respectivas médias do grupo,
sendo que o desempenho de Maria para salto em extensão é bastante
= 1 - 0,9772 = 0,0227
N°esperado de diabéticos = 0,0227 × 500 = 11,35
ruim.
Descreva o desempenho de Joana.
X ~ N(0,1)
X ~ N ( 100 , 10 2 )
Fonte: http://leg.ufpr.br/~silvia/CE055/node27.html
Método da curva de Gauss
Faixas de Referencia ou valores de referência
Este método pressupõe que a variável de interesse tem distribuição
Gaussiana (normal).
A construção da Faixa de referência é um procedimento que permite a
caracterização do que é típico em uma determinada população.
É empregado largamente em Ciências da Saúde, por exemplo, nos
resultados de exames de laboratório na determinação dos valores de
referência para a Hemoglobina, Hematócrito, Hematias, etc.
Portanto, antes de utilizá-lo, é necessário verificar se as observações
dos indivíduos sadios provém de uma distribuição normal ou
aproximadamente normal.
Uma faixa de referência, usual considera aproximadamente 95% dos
indivíduos sadios. Cujos limites, conforme vimos são:
Outras aplicações:
- determinação de níveis toleráveis de barulho
- caracterização dos níveis de poluição em uma região.
µ ± 1,96 σ
De maneira análoga, podem ser obtidas outras faixas de referência
compreendendo outras porcentagens de indivíduos sadios, tais como:
Fonte: Nogueira et al. 1996
etc.
90%
µ ± 1,64 σ
99%,
µ ± 2,58 σ
Faixas de Referencia
Exemplo:
Sabendo-se que a taxa de hemoglobina (g%) em mulheres sadias tem
distribuição N(14,2), construiremos faixas de referência que
englobem:
X = conteúdo de glicose com distribuição e X ~ N ( 100 , 10 2 )
P(-1,96 < Z ≤ 1,96) = 0.95
95 %
95% das taxas de hemoglobina
µ ± 1,96 σ 14 ± 1,96 *2 10.08, 17.92
80,4 < Glicose ≤ 119,6)
-1,96 < Z < 1,96
90% das taxas de hemoglobina
µ ± 1,64 σ 14 ± 1, 64 *2 10.71, 17.29
P(-2,58 < Z ≤ 2,58) = 0.99
99 %
-2,58 < Z ≤ 2,58
Distribuição Qui-quadrado
A distribuição chi-quadrado (χ2), é uma das mais usadas em
processos de inferência estatística. Assume valores não-negativos e
é assimétrica.
Se forem
, k distribuições normais padronizadas
(ou seja, média 0 e desvio padrão 1) independentes, então a
soma de seus quadrados é uma distribuição Chi-quadrado
com k graus de liberdade:
74,2 < Glicose ≤ 125,8)
Distribuição Qui-quadrado
Distribuição T de Student
A distribuição t de Student, desenvolvida por William Sealy
Gosset.
A distribuição t é uma distribuição de probabilidade teórica.
É simétrica, semelhante à curva normal padrão, porém com caudas
mais largas, ou seja, uma simulação da t de Student pode gerar
valores mais extremos que uma simulação da normal.
O único parâmetro v que a define e caracteriza a sua forma é o
número de graus de liberdade. Quanto maior for esse parâmetro,
mais próxima da normal ela será.
A distribuição t de Student aparece naturalmente no problema de se determinar
a distribuição da média de uma população (que segue uma distribuição
Normal), a partir de uma amostra. Neste problema, não se conhecee qual é a
média ou o desvio padrão da distribuição.
Supondo que o tamanho da amostra n seja muito menor que o tamanho da
população, temos que a amostra é formada por n variáveis aleatórias normais,
independentes X1, X2, ..., Xn, cuja média amostral :
é o melhor estimador para a média da população (µ), e se a variância amostral é
dada pela seguinte expressão:
A variável aleatória dada por
Segue uma distribuição t de Student com ν = n-1 graus de liberdade.
Distribuição T
Distribuição F
Também denominada distribuição F de Snedecor ou distribuição
Fisher-Snedecor, encontra aplicações em alguns testes estatísticos.
Consideram-se as variáveis aleatórias U e V tais que
• U e V são independentes.
• U tem distribuição χ2 com α graus de liberdade.
• V tem distribuição χ2 com β graus de liberdade.
A Figura abaixo apresenta curvas aproximadas das funções de
distribuição acumulada e de densidade de probabilidades para α =
5eβ=2
Média da distribuição F:
E(X) = β
β −2
se β > 2
Variância da distribuição F:
2 β (α + β − 2)
2
Define-se uma nova variável aleatória X tal que
X = (U / α) / (V / β)
Então X é tem distribuição F com α e β graus de liberdade ou
X ~F(α, β).
Fonte:http://www.mspc.eng.br/matm/prob_est358.shtml
Algumas propriedades
01) Se X tem distribuição t-student com ν graus de liberdade, então
X2 ~F(1, ν).
03) Sejam as seguintes amostras:
X1, X2, ... , Xm de uma população com distribuição normal de
média µ1 e variância σ12.
Y1, Y2, ... , Yn de uma população com distribuição normal de
média µ2 e variância σ22.
As variâncias das amostras são:
∑ (y i − y )
∑ (x − x )
S =
S = m i− 1
n −1
2
Então a variável definida por Z = s1 / s22 tem distribuição F com
m e n graus de liberdade. Esta propriedade pode ser usada para
testar a igualdade de variância entre as duas populações.
2
2
2
2
1
2
Var(X) =
α (β − 2) (β − 4)
2