gabarito - Walter Tadeu

COLÉGIO PEDRO II - CAMPUS SÃO CRISTÓVÃO III
APROFUNDAMENTO DE MATEMÁTICA – 2014
PROFESSORES: MARIA HELENA / WALTER TADEU
AULA 1: Geometria Plana – Áreas
QUESTÕES - GABARITO
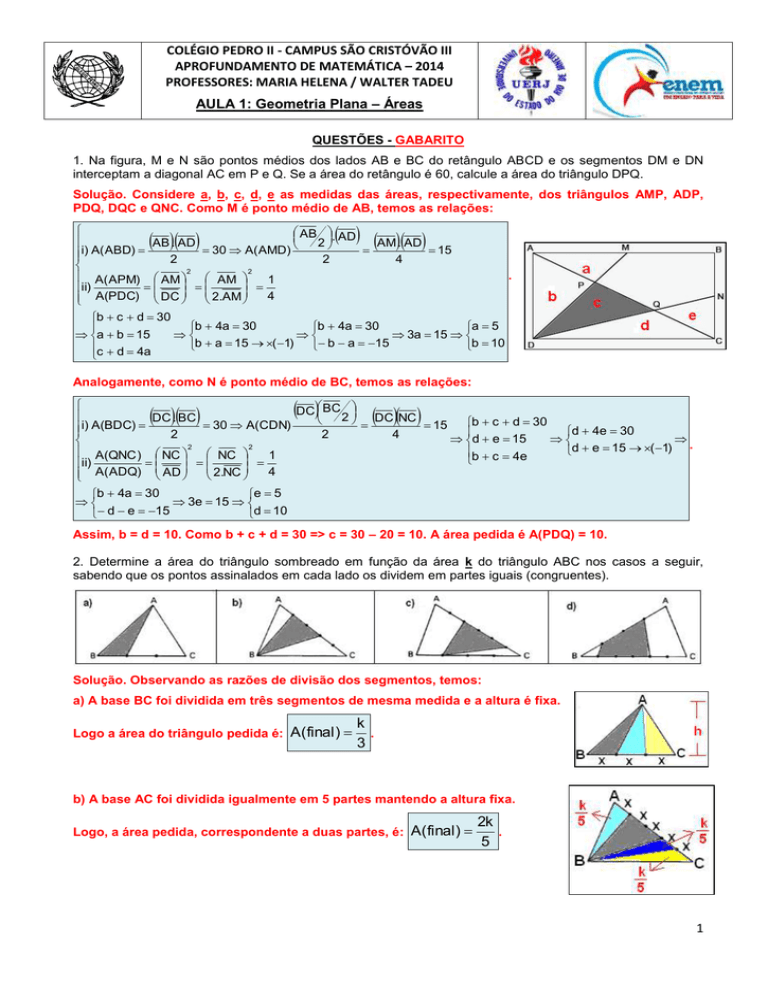
1. Na figura, M e N são pontos médios dos lados AB e BC do retângulo ABCD e os segmentos DM e DN
interceptam a diagonal AC em P e Q. Se a área do retângulo é 60, calcule a área do triângulo DPQ.
Solução. Considere a, b, c, d, e as medidas das áreas, respectivamente, dos triângulos AMP, ADP,
PDQ, DQC e QNC. Como M é ponto médio de AB, temos as relações:
    

 AB . AD

2
AB . AD
AM . AD
i) A( ABD) 
 30  A( AMD) 

 15


2
2
4

2
2
 A( APM)  AM   AM 
 
 1
 
ii)
 

4

 A(PDC)  DC   2.AM 
  
.
b  c  d  30
b  4a  30
b  4a  30
a  5

 a  b  15


 3a  15  
b  a  15  ( 1)  b  a  15
b  10
c  d  4a

Analogamente, como N é ponto médio de BC, temos as relações:
 

DC  BC 

2  DC NC
DC . BC

 30  A(CDN)

 15 b  c  d  30
i) A(BDC) 
d  4e  30

2
2
4
 d  e  15



2
2
d  e  15  ( 1) .

 A(QNC )  NC   NC 

b  c  4e
 
 1
 
ii)



A
(
ADQ
)
4
AD
2
.
NC

 


  
  
b  4a  30
e  5

 3e  15  
 d  e  15
d  10
Assim, b = d = 10. Como b + c + d = 30 => c = 30 – 20 = 10. A área pedida é A(PDQ) = 10.
2. Determine a área do triângulo sombreado em função da área k do triângulo ABC nos casos a seguir,
sabendo que os pontos assinalados em cada lado os dividem em partes iguais (congruentes).
Solução. Observando as razões de divisão dos segmentos, temos:
a) A base BC foi dividida em três segmentos de mesma medida e a altura é fixa.
Logo a área do triângulo pedida é: A( final ) 
k
.
3
b) A base AC foi dividida igualmente em 5 partes mantendo a altura fixa.
Logo, a área pedida, correspondente a duas partes, é: A( final ) 
2k
.
5
1
c) A base BC foi dividida em 4 em partes iguais de medida “y”, mantendo a altura em relação a essa
base fixa.
Logo, uma dessas partes possui área valendo A 1 
A área restante vale A  A 1  k 
k
.
4
k 4k  k 3k


. Esta área restante teve sua
4
4
4
base AC dividida em 6 partes iguais e mantendo sua respectiva altura fixa.
A área pedida (3 partes) é: A( final ) 
3  3k  9k 3k
.  

.
6  4  24 8
d) A base BC foi dividida em 6 em partes iguais de medida “y”, mantendo a altura em relação a essa
base fixa. A área (duas partes) vale A 1 
2k k
2k
 . A área restante é A 
.
6 3
3
A base AB foi dividida em 4 partes iguais, mantendo-se fixa a altura relativa a
essa base.
A área corresponde a duas partes da área restante (a + b) é: A 2 
A área indicada pela letra c corresponde a A c 
A área S (a + b + c) pedida é: A( final ) 
2  2k  k
.   .
4 3  3
3  1  2k  k
.    .
4  4  3  8
k k 8k  3k 11k
 

.
3 8
24
24
3. Determine a área da região sombreada em função da área k do paralelogramo ABC nos casos a seguir,
sabendo que os pontos assinalados em cada lado os dividem em partes de medidas iguais.
Solução. Observando as razões de divisão dos segmentos, temos:
a) A diagonal AD divide o paralelogramo em duas áreas iguais a
k
.
2
A base CD foi dividida em seis segmentos de mesma medida e a altura é
fixa. A área de cada um dos triângulos de vértice em A e base x é
k k
6k  k 5k
1k  k



. A área restante será:
.
 
2 12
12
12
6  2  12
A base AC foi dividida em 5 partes iguais com altura fixa. Logo, a área
representada por a vale: A(a) 
1  5k  k
.
 
5  12  12
A área representada pela letra b vale: A(a) 
4  3   5k  k
 .   .
5  5   12  5
Logo a área do triângulo pedida é: A( final )  a  b 
k k 5k  12k 17k
 

.
12 5
60
60
2
b) As alturas dos triângulos assinalados são as mesmas do paralelogramo. Logo, temos:

 AB .h

4
AB .H k

i
)
A
(
a
)




k
k 3k  k 4k k
k  k
2
8
8
 Área(pedida)  2.  
 



8
12
4
12
12
12 3 .


 
DC



.
h

6 
DC .H k
ii) A(b)  



2
12
12
b

c

d

30

b  4a  30
b  4a  30
a  5

 a  b  15


 3a  15  
b  a  15  ( 1)  b  a  15
b  10
c  d  4a

 
 
4. Na figura, ABCD é um paralelogramo de área S e M é ponto médio
sombreada de S.
Solução. Observando as razões de divisão dos segmentos, temos:
CD determine a área da região

S
S

i) A(BDC) 
2
a  c  4

S


ac

S

DC
A
(
BDC
)
S
S



4 
 A(BMC) 
 2   b  c   
.
ii) MC 
2
2
2
4
2


4a  c  S

 A(EMC)  MC 2  MC 2 1
b  4a
2
ii)

 
 
 




4
 A(EAB)  AB   2.AB 
 4a  a 
S
S
S
 3a   a 
4
4
12
5. Se a área do triângulo ABCD é k e os pontos assinalados em cada lado o dividem em partes iguais,
determine a área do triângulo sombreado em função de k.
Solução. Considere as medidas de áreas a, 2a, 3b e 2b. Observando as divisões e as respectivas
razões, temos:
2k

3a  2b  5  (5) 15a  10b  2k
2k
4k

 13a 


2k  13a  2k 
.
k
3
3

2
a

10
b


a  5b   ( 2)

3

3
4k
 4k  8k
a
 2a  Área(pedida)  2.  
39
 39  39
6. Se os pontos R, S, T, U, V e X dividem AB , BC e AC , respectivamente, em três partes iguais, determine
a área do triângulo sombreado em função da área k do triângulo ABC.
Solução. Observando as analogias nos casos, temos:
k

3a  y  3  ( 3)  9a  3 y  k


2k 
2a  3 y  2k
2a  3 y  3

3
.
k
k
 7a    a  .
3
21
k 3k 18k 4k
Logo, y  


3 21 21 21
Temos: 3y + 9a – 3a + A(EDF) = K.
Calculando a área, vem:
 4k 
k 
A(EDF)  k  3.   6. 
21
 
 21
.
18k 21k  18k 3k k
A(EDF)  k 



21
21
21 7
3
7. (UERJ) Considere uma placa retangular ABCD de acrílico, cuja diagonal AC mede 40 cm. Um estudante,
para construir um par de esquadros, fez dois cortes retos nessa placa nas direções AE e AC, de modo que
DÂE=45º e BÂC=30º, conforme ilustrado a seguir. Após isso, o estudante
descartou a parte triangular CAE, restando os dois esquadros. Admitindo
3  1,7 que a espessura do acrílico seja desprezível e que a área, em
cm², do triângulo CAE equivale a:
a) 80
b) 100
c) 140
d) 180
Solução. Identificando os valores de x, y e z na figura temos:
i) y = 20cm pois é cateto oposto ao ângulo de 30º no triângulo
retângulo ABC. Também será o valor da altura do triângulo AEC.
ii) x = 20 3  20.(1,7)  34cm , pois é oposto ao ângulo de 60º do triângulo ABC. Vale a metade da
hipotenusa multiplicado pela raiz de 3.
iii) DE = y = 20cm, pois é cateto do triângulo retângulo isósceles ADE. Logo z = EC = 34 – 20 = 14cm.
A área do triângulo CAE vale: A 
EC  AD 14  20

 140cm 2 .
2
2
8. (ENEM) O tangram é um jogo oriental antigo, uma espécie de quebra-cabeça, constituído de sete peças: 5
triângulos retângulos e isósceles, 1 paralelogramo e 1 quadrado. Essas peças são obtidas recortando-se um
quadrado de acordo com o esquema da figura 1. Utilizando-se todas as sete peças, é possível representar
uma grande diversidade de formas, como as exemplificadas nas figuras 2 e 3. Se o lado AB do hexágono
mostrado na figura 2 mede 2cm, então a área da figura 3, que representa uma “casinha”, é igual a:
a) 4cm2
b) 8cm2
c) 12cm2
d) 14cm2
e) 16cm2
Solução. A casinha é feita com as mesmas peças da figura 1 e da
figura 2. Logo, as áreas são as mesmas. O lado do quadrado
construído na Figura 1 é a hipotenusa a do triângulo retângulo
isósceles maior. O lado AB do hexágono da figura 2 mede 2cm e é
formado por um dos triângulos retângulos isósceles menores com
catetos de mesma medida do quadrado. Essa medida é a mesma do
cateto do triângulo retângulo maior. Temos:
a 2  2 2  2 2  4  4  8cm2
Área(quadrado )  Área(ca sinh a)  a 2  8cm2
.
9. (ENEM) Uma empresa produz tampas circulares de alumínio para tanques cilíndricos a partir de chapas
quadradas de 2 metros de lado, conforme a figura. Para 1 tampa grande, a
empresa produz 4 tampas médias e 16 tampas pequenas. As sobras de
material da produção diária das tampas grandes, médias e pequenas dessa
empresa são doadas, respectivamente, a três entidades: I, II e III, para
efetuarem reciclagem do material. A partir dessas informações, pode-se
concluir que:
a) a entidade I recebe mais material do que a entidade II.
b) a entidade I recebe metade de material do que a entidade III.
c) a entidade II recebe o dobro de material do que a entidade III.
d) as entidades I e II recebem juntas, menos material do que a entidade III.
e) as três entidades recebem iguais quantidades de material.
Solução. As chapas possuem área igual a 4m2. Os raios das tampas grande, média e pequena são,
respectivamente, 1m, 0,5m e 0,25m. Calculando as sobras em cada produção, temos:


área : 4. (0,5) 2  4.0,25   m 2
.
4 Tampas (média ) : 
2
sobra : 4   m
área : (1) 2   m 2
.
Tampa (grande ) : 
2
sobra : 4   m


área : 16. (0,25) 2  16.0,0625   m 2
.
16 Tampas (pequenas ) : 
2


sobra
:
4


m

As sobras são as mesmas nas três produções.
4
10. (UERJ) Um tabuleiro retangular com pregos dispostos em linhas e colunas igualmente espaçadas foi
usado em uma aula sobre área de polígonos. A figura abaixo representa o tabuleiro com um elástico fixado
em quatro pregos indicados pelos pontos A, B, C e D.
Considere u a unidade de área equivalente ao menor quadrado que
pode ser construído com vértices em quatro pregos do tabuleiro.
Calcule, em u, a área do quadrilátero ABCD formado pelo elástico.
Solução. Fechando um retângulo de dimensões 9 x 5, temos uma
área de 45. São identificados em volta do quadrilátero quatro
triângulos retângulos: 1, 2, 3 e 4. Calculando suas áreas e a
diferença em relação ao retângulo, temos:
(3)( 4)

T(1)  2  6

.
T(2)  (5)(1)  2,5

2
 Soma(Triângulos )  6  2,5  7  4  19,5  A(Quadriláte ro )  45  19,5  25,5

T(3)  (2)(7)  7

2

(2)( 4)
T( 4) 
4
2

11. (UERJ) Considere um setor circular AOC, cujo ângulo central Ө é medido em radianos. A reta que
tangencia o círculo no extremo P do diâmetro CP encontra o prolongamento do diâmetro AB em um ponto Q,
como ilustra a figura. Sabendo que o ângulo Ө satisfaz a igualdade tgӨ = 2Ө, calcule a razão entre a área do
setor AOC e a área do triângulo OPQ.
Solução. O triângulo OPQ é retângulo em P, pois é ponto de tangência. Encontrando as áreas
respectivas e a razão pedida, temos:
(QP ).( OP )

A OQP 
(OP.tg).( OP ) (OP )2.tg R2.2
2
i) 
 A OQP 


2
2
2
tg  QP  QP  OP.tg
OP

 
 
2  R2
R2 . R2 .
ii) 
 A AOC 

2
2
  A AOC
2
R
A AOC
R 2 2
1
 22 
.

A OQP R .2
2 R2.2 2
2
.
12) (ENEM) Ao morrer, o pai de João, Pedro e José deixou como herança um terreno retangular com
medidas de 3km x 2km que contém uma área de extração de ouro delimitada por um quarto de círculo de
raio 1 km a partir do canto inferior esquerdo da propriedade. Dado o maior valor da área de extração de ouro,
os irmãos acordaram em repartir a propriedade de modo que cada um ficasse com a terça parte da área de
extração, conforme mostra a figura. Em relação à partilha
proposta, constata-se que a porcentagem da área do terreno
que coube a João corresponde, aproximadamente, a:
3
3
(considere
a) 50%
b) 43%
c) 37%
d) 33%
e) 19%
Solução. O quarto de círculo corresponde a um setor de
90º. A parte que coube a João é um triângulo retângulo
com ângulo de 30º e 60º. O terreno possui área igual a
(2).(3) = 6km². Calculando a área da parte de João e
verificando o percentual em relação ao terreno, temos:

tg30º 
i) 
tg30º 

y
2
3
 0,58
3

y
(2)(1,16)
 0,58  y  1,16km ; ii) Área(João) :
 1,16km²
2
2
iii)
.
Área(João)
 0,193  19%
Área(Terreno )
5