MÓDULO 6 – PONTOS NOTÁVEIS Chama
Propaganda
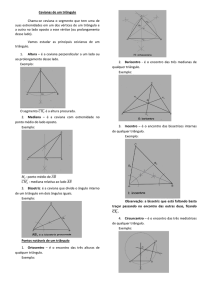
MÓDULO 6 – PONTOS NOTÁVEIS Altura - Ortocentro Chama-se ceviana de um triângulo, todo segmento com uma extremidade num vértice desse triângulo e a outra num ponto qualquer da reta suporte do lado oposto. Altura de um triângulo é qualquer ceviana perpendicular ao lado ao qual ela é relativa. Os segmentos AL, AP e CQ são cevianas do triângulo ABC acima. AL e AP são cevianas relativas ao vértice A, ou ao lado BC, enquanto CQ é relativa ao vértice C, ou ao lado AB. Os pontos L, P e Q são os pés dessas cevianas. As alturas do triângulo podem ser cevianas externas a ele (no triângulo obtusângulo) ou podem até mesmo coincidir com lados (no triângulo retângulo). Mediana – Baricentro Mediana de um triângulo é qualquer ceviana com o pé no ponto médio de um lado AB e CB são alturas do triângulo retângulo acima Propriedade. As retas suportes das alturas do triângulo concorrem num mesmo ponto H, chamado ortocentro. O ortocentro pode ser interno, externo ou até coincidir com um vértice do triângulo. Mediatriz – Circuncentro AG BG CG 2 = = = GM GN GL 1 Propriedade. As três medianas do triângulo concorrem num mesmo ponto G, denominado baricentro do triângulo. O baricentro divide cada mediana em segmentos proporcionais a 2 e 1. Mediatriz, como já definimos antes, é a reta perpendicular a um segmento de reta, passando pelo ponto médio do mesmo. Bissetriz Interna – Incentro Bissetriz interna de um triângulo é qualquer ceviana que divide um ângulo interno em dois ângulos congruentes. Propriedade. As mediatrizes dos lados do triângulo concorrem num mesmo ponto O denominado circuncentro. O circuncentro é o centro da circunferência circunscrita ao triângulo. Propriedade. As bissetrizes do triângulo concorrem num mesmo ponto I, chamado incentro. O incentro é o centro da circunferência inscrita no triângulo. Observação O circuncentro também pode ser externo ao triângulo (no triângulo obtusângulo) ou pertencer a um lado (no triângulo retângulo). Mais adiante estudaremos esses casos.
