MÓDULO DE WEIBULL

F. Jorge Lino
Módulo de Weibull
MÓDULO DE WEIBULL
F. Jorge Lino
Departamento de Engenharia Mecânica e Gestão Industrial da Faculdade de Engenharia da Universidade do Porto,
Rua Dr. Roberto Frias, 4200-465 Porto, Portugal, Telf. 22508704/42, [email protected], www.fe.up.pt/~falves
1.
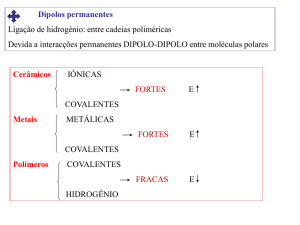
Natureza Estatística da Fractura: Análise de Weibull
O facto de Leonardo da Vinci repetir várias vezes as suas experiências para verificar os
resultados obtidos, mostra a sua preocupação com a natureza estatística dos fenómenos de
fractura. Geralmente, a variação estatística de um dado valor de uma propriedade mecânica (por
exemplo, a resistência à fractura) depende de erros inerentes às medições, tais como variações no
alinhamento da amostra e do meio ambiente do ensaio, e variações inerentes às propriedades do
material. Nesta análise, apenas se considera a última fonte de variação estatística das
propriedades de fractura. Sendo assim, um evento de fractura dependerá da probabilidade de que
uma fissura de uma dada dimensão e orientação esteja presente quando é aplicada uma tensão
específica. Por exemplo, considere-se a existência dos 4 tipos diferentes de fissuras
representados na figura seguinte.
F
A
a
B
b
F
Admita-se ainda que os comprimentos das fissuras A e B são iguais aos comprimentos das
fissuras a e b, respectivamente, e que cada defeito actua independentemente dos outros três. A
Fevereiro 2006
1
F. Jorge Lino
Módulo de Weibull
fractura ocorrerá quando σ B atingir um valor crítico. Uma vez que A<B, não ocorrerá fractura
associada à fissura A. Além disso, uma vez que as fissuras a e b são paralelas à direcção da força
aplicada, também não ocorrerá fractura associada a esta fissuras, mesmo sendo b=B.
Consequentemente, a probabilidade de fractura dependerá somente da existência da fissura do
tipo B.
Um elemento fundamental no projecto e fabrico de um componente diz respeito à sua
fiabilidade (geralmente determinada por questões de segurança e/ou económicas), pelo que se
torna necessário conhecer a probabilidade estatística de que um dado evento de fractura ocorra.
Para o caso da fractura de fios frágeis, tais como os estudados por da Vinci, a fractura dependerá
somente do comprimento do fio: quanto maior for o comprimento do fio, maior será a tendência
para que um defeito crítico que cause fractura possa estar presente. Esta teoria “do elo mais
fraco” significa que a fractura é dependente do volume de material do fio, sendo este
proporcional ao comprimento do fio (de um dado diâmetro). Tendo em conta que um sólido
possui maior quantidade de defeitos na sua superfície do que no seu interior (por exemplo,
defeitos produzidos por acabamento superficial ou corrosão superficial), a probabilidade de
fractura dependerá apenas da área total superficial do componente.
Para questões de projecto, é geralmente mais importante determinar a probabilidade de que
uma propriedade de um componente exceda um valor limite do que determinar um valor
particular tal como a tensão média de ruptura. A experiência demonstrou que uma distribuição
normal (Gaussiana) dos valores de uma determinada propriedade de um material dúctil fornece
uma caracterização razoavelmente rigorosa do comportamento do material; o mesmo não se
poderá dizer para o caso de um sólido frágil. Como tal, serão necessárias outras teorias
estatísticas que considerem a variabilidade da tensão e da resistência à fractura dos sólidos
frágeis. A discussão que se segue, baseada na análise de Weibull, caracteriza a probabilidade de
sobrevivência de um dado componente em função do seu volume e da tensão aplicada.
Para o caso de um veio frágil de comprimento L, sujeito a uma tensão σ, a probabilidade
de sobrevivência é dada por S(L). Para uma outra peça no mesmo material com comprimento L’,
a probabilidade de sobrevivência à mesma tensão é S(L’). Se se juntarem “x” peças deste veio, a
probabilidade total de sobrevivência, para a mesma tensão, será S(L0)x, sendo L0 o comprimento
de cada unidade. (A probabilidade de sobrevivência dos “x” segmentos do veio é análoga à
probabilidade de obter um resultado específico com uma série de lançamentos de uma moeda.
Uma vez que a probabilidade de obter uma cara é 1/2, a probabilidade de obter “duas” caras será
Fevereiro 2006
2
F. Jorge Lino
Módulo de Weibull
1/4. Para “três” caras, a probabilidade será 1/8, ou (1/2)3). Se a distribuição de fissuras em cada
volume for a mesma, a probabilidade de sobrevivência do veio será:
S (V ) = S(V0 )
x
,
(1)
sendo V0 o volume de cada unidade do sólido. Utilizando logaritmos e rearranjando a equação
(1), teremos
(
)
S (V ) = exp x ln[S(V0 )] .
(2)
Weibull definiu o risco de ruptura R como sendo
R = − x ln[S(V0 )] ,
(3)
S (V ) = exp (− R) .
(4)
e consequentemente
Para um volume V, demonstra-se que o risco de ruptura é
R = ∫ f (σ )dV ,
(5)
V
sendo apenas função da tensão.
Alem disso, segundo Weibull
 (σ − σ u )
f (σ ) = 
 ,
 σ0 
m
(6)
onde:
σ
- tensão aplicada
σu
- tensão abaixo da qual há 0% de probabilidades de ruptura. Isto implica a existência de
um limite superior para o tamanho dos defeitos presentes no material. (No caso da
Fevereiro 2006
3
F. Jorge Lino
Módulo de Weibull
fadiga em aços, σ u = σ fadiga . Para os cerâmicos frágeis, σ u = 0 uma vez que qualquer
tensão de tracção poderá causar fractura. Para σ < 0 não é previsível a ocorrência de
fractura, uma vez que tensões de compressão tendem a fechar a fissura.).
σ0
- tensão característica, sendo semelhante à tensão (resistência) média do material.
m
- módulo de Weibull que caracteriza a variância na resistência do material, sendo
análogo ao desvio padrão da resistência dos materiais.
Valores crescentes de m reflectem o comportamento de um material mais homogéneo, com
níveis de resistência, para um dado componente, mais previsíveis. No limite, quando m tender
para infinito, a probabilidade de fractura, para todos os níveis de tensão < σ 0 , será zero. Quando
σ = σ 0 , a probabilidade de fractura será 1. Contrariamente, quando m se aproxima de 0, R tende
para a unidade, ocorrendo fractura com igual probabilidade para qualquer nível de tensão. Para
todos os outros valores (0<m<∞), o risco de fractura será também função do módulo de Weibull.
Por exemplo, se σ u = 0 e f (σ ) constante, teremos para um volume unitário e para um risco de
fractura de 0.5:
σ

0.5 =  R = 0.5 
 σ0 
m
,
(7)
e consequentemente, o nível de tensão correspondente a um risco de ruptura de 0.5 é
1
σ R= 0.5 = (0.5) m σ 0 .
(8)
Quando m=2 ou m=20, σ R = 0.5 será 0.71σ 0 e 0.97σ 0 , respectivamente, ou seja, quanto mais
baixo for o valor de m, menor será a tensão admissível para assegurar a mesma probabilidade de
ruptura. Alem disso, é perigoso considerar o mesmo coeficiente de segurança (que traduz uma
fracção de σ 0 ) para dois materiais frágeis diferentes (m diferente), uma vez que a mesma
probabilidade de fractura dos dois materiais corresponde a diferentes fracções das suas tensões
médias.
Fevereiro 2006
4
F. Jorge Lino
2.
Módulo de Weibull
Efeito do Tamanho na Natureza Estatística da Fractura
Combinando as equações (4) a (6), a probabilidade de sobrevivência para uma tensão
uniforme é dada por
  σ − σ  m 
u
S (V ) = exp − V 
  .
  σ 0  
(9)
O mesmo é dizer que o risco de falha F é
  σ − σ  m 
u
F = 1 − exp −V 
 .
  σ 0  
(10)
Considerando o duplo logaritmo da equação (9) e rearranjando, poderá obter-se uma
relação linear entre a probabilidade de sobrevivência e a tensão aplicada num componente, sendo
o declive do gráfico caracterizado pelo módulo de Weibull, m (ver por exemplo a figura
seguinte).
A equação (9) mostra que para a mesma probabilidade de sobrevivência, a resistência à
fractura de um dado material varia com o volume do componente. Por exemplo, se σ u = 0 ,
V1 (σ 1 ) = V2 (σ 2 )
m
Fevereiro 2006
m
,
(11)
5
F. Jorge Lino
Módulo de Weibull
e
1
σ 1  V2  m
= 
.
σ 2  V1 
(12)
Logicamente, que para uma probabilidade igual de sobrevivência, quanto maior for o
volume do componente, mais baixa é a tensão necessária para ocorrer a fractura (ver figura
anterior).
Exemplo
Considere a utilização de duas peças fabricadas em materiais cerâmicos frágeis numa dada
aplicação. Os módulos de Weibull para os dois materiais são 2 e 10, respectivamente. Se σ A e
σ B representarem as tensões necessárias para a mesma probabilidade de sobrevivência de
provetes laboratoriais dos dois materiais, de quanto deverão ser alteradas as tensões respectivas
se o volumes dos componentes reais de cada material forem 10x maiores do que os dos provetes
laboratoriais?
Em cada caso, a tensão necessária para a mesma probabilidade de sobrevivência varia com
a relação volume provete/componente (ver equação (12)). Para o caso do material com módulo
de Weibull mais elevado, a tensão para a mesma probabilidade de sobrevivência diminuirá
1.26x, considerando o volume do componente 10x maior de que o do provete. Mais preocupante
será a tensão necessária para a mesma probabilidade de sobrevivência do outro material, a qual
diminuirá 3.16x, quando o volume aumentar 10x. Obviamente que o material com o maior grau
de dispersão nas propriedades mecânicas (isto é, módulo de Weibull mais baixo) será mais
sensível ao efeito de tamanho.
A probabilidade de sobrevivência dependerá também da existência de gradientes de tensão
e do volume de material associado que fica sujeito à tensão máxima no componente ou provete.
Por exemplo, espera-se que a probabilidade de fractura seja maior em tracção do que em
compressão. Uma força de tracção produz a mesma tensão através de toda a área da secção
transversal do componente, enquanto que forças de flexão originam uma tensão máxima somente
na parte exterior do veio. Considerando os volumes respectivos dos locais sujeitos a tensões
Fevereiro 2006
6
F. Jorge Lino
Módulo de Weibull
máximas de tracção e de flexão, poderá ser demonstrado que para a mesma probabilidade de
sobrevivência os níveis de tensão de fractura nas amostras sujeitas a tracção e flexão serão
diferentes. Considere-se a relação entre forças de tracção e flexão para a mesma probabilidade de
sobrevivência:
1
σ 3pontos
2 m
= {2(m + 1) } .
σ tracção
(13)
Se o módulo de Weibull de dois materiais for 2 e 10, respectivamente, tal como foi
exemplificado no exemplo anterior, a relação tensão flexão/tracção para uma probabilidade igual
de sobrevivência será 4.24 e 1.73, respectivamente. A barra sujeita à flexão terá maior resistência
uma vez que o volume de material sujeito à tensão máxima é menor do que o da barra sujeita à
tracção. Isto é verdade especialmente para os casos em que m é baixo. Contrariamente, à medida
que m se aproxima do infinito, as propriedades das barras sujeitas à tracção e compressão
convergem para o mesmo valor.
Fevereiro 2006
7