Gabarito Extensivo – MATEMÁTICA volume 1 – Frente D

Gabarito Extensivo – MATEMÁTICA
volume 1 – Frente D
01)
8x − 40 = 6x − 20
8x − 6x = −20 + 40
2x = 20
x = 10
• 8x − 40 = 8.10 − 40 = 80 − 40 = 40°
• 6x − 20 = 6.10 − 20 = 60 − 20 = 40°
02)
Ponteiro pequeno (horas):
30° - 1 hora = 60 minutos
12° - ?
30 60
=
12 x
x = 24 min
Portanto, 1h24min
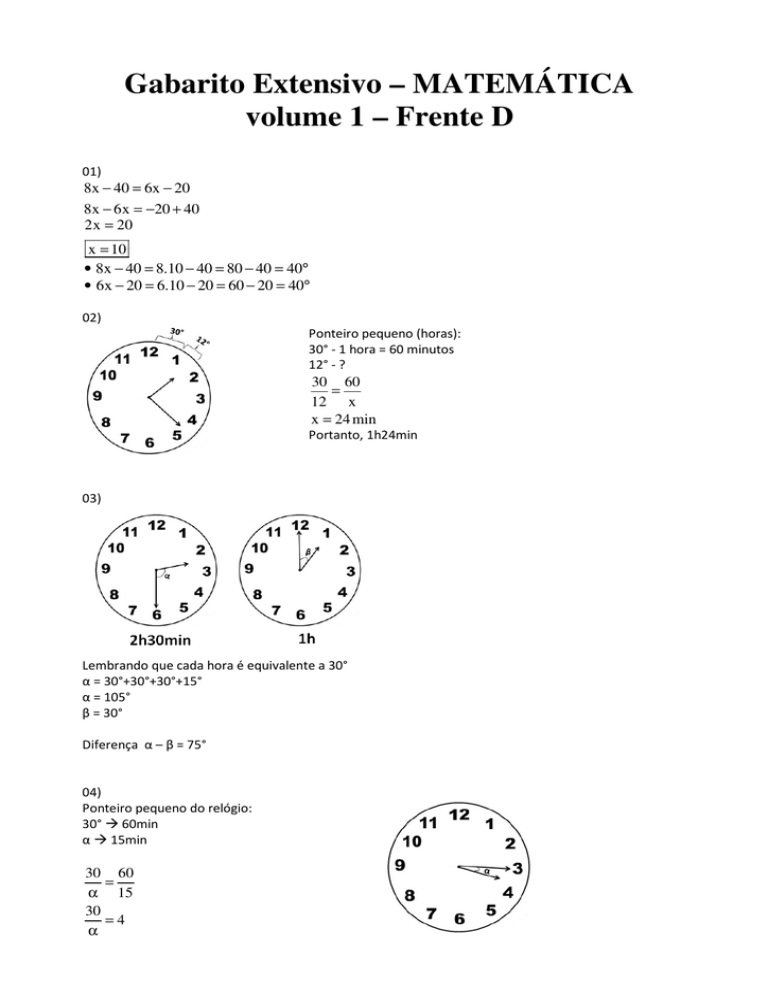
03)
Lembrando que cada hora é equivalente a 30°
α = 30°+30°+30°+15°
α = 105°
β = 30°
Diferença α – β = 75°
04)
Ponteiro pequeno do relógio:
30° 60min
α 15min
30 60
=
α 15
30
=4
α
4α = 30
α = 7, 5°
OBS:
1°60’
0,5°x
x = 30’ = 30 minutos
Portanto,
α = 7°30 '
05)
(A + C) − (B + D) = (22
°32 '15''
+ 75°01'52
°49 ' 47''
+ 32º 44 ' 20
'') − (17
'')
i
i)
ii
ii)
22°32 '15 ''
17°49 ' 47 ''
+ 75°01'52 ''
97°33'67 ''
+ 32º 44 ' 20 ''
49°93'67 ''
OBS: 60’’ 1’
OBS: 60’’ 1’ 49°93'67 '' = 49°94'07 ''
97°33'67 '' = 97°34 '07 ''
60’ 1° 49°94 '07 '' = 50°34 '07 ''
Portanto, i-ii =
i − ii :
97°34 '07 ''
− 50°34 '07 ''
47°00 '00 ''
i − ii = 47°
06)
Considerando o deslocamento do ponteiro a partir das 12h (pequeno).
Ponteiro menor
Ponteiro maior
360 12h
=
x
2h
12x = 360.2
30° 60 min
=
y
32 min
60y = 32.30
x = 60º
y = 16º
Portanto, entre 12h e 2h32min o ponteiro desloca-se x+y = 60°+16° = 76°. Sendo que o ponteiro maior
desloca-se 360° em 1 hora, logo:
360° 1h 60min
360° 60min
z 32min
360 60
=
z
32
60z = 360.32
z = 192°
Portanto, a diferença entre eles é o menor ângulo:
192° − 76° = 116°
07)
Ponteiro menor
Ponteiro Maior
360º 12h
=
x
1h
12x = 360
30º 60 min
=
x ' 50 min
60x ' = 30.50
x = 30°
x ' = 25°
OBS: Cada hora = 30°
Logo, α = 30°+30°+30°+25°=115°
α = 115°
08)
10h10min
P. menor
P. maior
30º 60
=
x
10
x = 5°
360º 60
=
x'
10
x ' = 60°
Portanto,
α = 180° − P.menor – P.maior
α = 180° − 5° − 60°
α = 115°
09)
30º 60 min
=
y
15 min
360º 60 min
=
x
15 min
x = 90°
y = 7,5° → y = 7°30 '
Menor ângulo: 90° - 7°30’ = 82°30’
10)
360° = 2πrad
rad =
360
360
=
= 57,3° → 1rad = 57,3°
2π 2.3,14
11)
2πrad
3
360° 2πrad
=
120°
x
3x = 2πrad
a)
x=
2πrad
3
5πrad
4
360° 2πrad
=
225°
x
8x = 10πrad
b)
x=
10πrad 5πrad
=
8
4
d)540°
e)112,5°
360° 2πrad
=
x
3πrad
2x = 360.3
360° 2πrad
=
5π
x
rad
8
360°
8
= 2.
x
5
x = 112,5°
x = 540°
12) No problema considerar x-56° x + 56°
Ângulos opostos pelo vértice são iguais, logo
3x − 80 = x + 56
3x − x = 80 + 56
2x = 136
x = 68°
4πrad
5
360° 2πrad
=
144°
x
5x = 4πrad
c)
x=
4π
rad
5
13)
= 180° = π
AOD
+ MON
= AOD
POD
2θ + 2β + 2α = π
2(θ + β + α ) = π
π
θ + β + α = rad
2
14)
a) 54°36’31’’
b)
32°53'36 ''
+ 21°42 '55''
16°29'20 ''
7
53°95'91''
60’’=1’ 53°96'31''
60’=1° 54°36'31''
Transformando tudo em segundos.
1°60’
16°x
x=960’+29’=989’20’’
1’60’’
989’x
x = 59340’’+20
x = 59360’’
Portanto,
59360 ÷ 7 = 8480 ''
8460 ''
20 ''
60
→ 141' 20 ''
→
120 '
21' 20 ''
60
→ 2°21' 20 ''
→
c) 5.(34°28’40’’)
Primeiro, transformar tudo em segundos:
x = 124120’’.5
x = 620600’’
x=
620580 ''
20 ''
60
x = 10343’20’’
10320 '
23' 20 ''
60
x = 172°23' 20 ''
x=
d)
24°31' 25 ''
OBS:
− 12°51' 42 ''
31’ = 30’+60’’
↓
25’’+60’’=85’’
24°30 '85 ''
− 12°51' 42 ''
↓
OBS:
24° = 23° + 60’
30’+60’=90’
23°90 '85 ''
− 12°51' 42 ''
11°39 ' 43''
15) Falta indicar no problema o ângulo 135°40’
2
3
1°) 2. (x + 18°)
2°)
2
(x + 18°)
3
3°) x+18°
4°) x
Portanto,
4
2
(x + 18°) + (x + 18°) + x + 18° + x = 135°40 '
3
3
4x
2x
+ 24° +
+ 12° + 2x + 18° = 135°40 '
3
3
4x 2x
+
+ 2x = 135°40 '− 24° − 12° − 18°
3
3
4x + 2x + 6x
= 81°40 '
3
12x = 3(81
°40
')
81°+
2°
3
245°
≈ 20, 40°
12
x = 20°25'
x=
16)
x
+ 18°
4
4x − 144 x + 72
=
4
4
3x = 216
x − 36° =
x = 72°
x
72
+ 18 =
+ 18 = 36°
4
4
Portanto,
y = 180° − 36° = 144°
y = 144°
17)
3α + β = 3.45+60=195°
18)
x = 180-95
x=85°
19)
X=83°
20) C
π
  π−x 
3 − x  = 

2
  3 
3π
π−x
− 3x =
2
3
9π − 18x 2π − 2x
=
6
6
7 π = 16x
x=
7π
16
21)
y = 180° - 90°
y = 90°
22)
α = 40° e β = 65°
x + y =?
x = 180° – 75° = 105°
y= 180 – 40° = 140°
x+y=105+140 = 245°
23) B
Onde r//u
x+20°=120°
x = 100°
x = y = 100°
2x+3y=?
2.100+3.100=500
24)
θ = 180°-120°-40°
θ = 20°
25)
Bissetriz 46°
Um dos ângulos = 32°
Outro ângulo = x
x + 16 = 46
x = 46 – 16
x = 30° Só que este ângulo é a metade da bissetriz, logo o 2° ângulo é 30x2 = 60°
26)
r//s
x=180°-68°-40°
x=172°
27)
5a + 3a − a + 3a − a = 180°
9a = 180
180
a=
9
a = 20
Sendo AC=AB,
5a + 180 − x + 180 − x = 150
5a − 2x = −180
5.20 − 2x = −180
100 − 2x = −180
−2x = −180 − 100
280
2
x = 140°
x=
28)
Complemento → 90° − x → 2.(90° − x)
 180° − x 
Suplemento → 180° − x → 

5


180° − x
180° − 2x =
5
180.5 − 10x = 180 − x
10x − x = 900 − 180
9x = 720
720
x=
9
x = 80°
360° − x = 360° − 80° = 280°
29) B
AC está para BC assim como DF=DE e EF está para
EF.
X está para 8 assim como 5+x está para x-10
x(x-10)=8(5+x)
x2-10x=40+8x
x2-18x-40=0
x’=20
x’’= -2 Não serve.
AC está para BC assim como GI está para HI.
x y
20 y
=
→
=
8 10
8 10
y = 25
Logo, x+y = 20 + 25 = 45
Resposta: (B) entre 41 e 46
30)
90 − A
=5
180 − B
90 − A = 900 − 5B
− A = 900 − 90 − 5B
− A = 5B − 810
Consecutivos.
2A + 2B = 360°
2(A + B) = 360
A + B = 180
A = 180 − B
180 − B = 5B − 810
6B = 990
B = 165°
A = 180° − 165°
A = 15°
A = 15° e B = 165°
31) B = 85°
32)
Observe AF e BF conforme a figura
OBS: Os triângulos CEF e DEF, temos:
= m(BCE)
+ m(CEF)
+ m(DEF)
+ m(AED)
=
m(CFD)
+ m(CED)
+ CDE
= 130O
m(BCE)
Portanto,
= 130o
AFB
180 − 130
= 25o
2
33)
Α = 10o +60o=70o
Se u’ e t’ que passam pelos pontos A e B são
paralelas às retas r e s.
34)
7
e
2
180(n − 2) 7 360
= .
n
2 n
180(n − 2) = 7.180
i=
n =7+2
n =9
35)
n=9
n(n − 3) 9(9 − 3)
=
= 27
2
2
d = 27
d=
36)
n(n − 3)
= 170
2
n 2 − 3n = 340
n 2 − 3n − 340 = 0
n=
−b ± b 2 − 4ac
2a
3 ± (−3) 2 − 4.1.(−340) 3 ± 1369 +3 ± 37
n=
=
=
2.1
2
2
n’=20
n’’=-17
i=
180(20 − 2)
= 162o
20
37)
n(n − 3)
= 2n
2
n 2 − 3n = 4n
n 2 − 3n − 4n = 0
n 2 − 7n = 0
n(n − 7) = 0
n'=0
n``= 7
38)
z + w = 190o
z
+ w + 2x + 2y = 360o
190o
190o + 2x + 2y = 360o
2x + 2y = 170o
x + y = 85o
α + x
+ y = 180o
85o
α + 85o = 180o
α = 95o
39)
180 (n − 2) = 2160
216
= 12
18
n = 2 + 12
n−2=
n = 14
n(n − 3) 14(14 − 3)
D=
=
= 7.11 = 77 diagonais.
2
2
40)
n(n − 3)
= n +3
2
n 2 − 3n = 2n + 6
n 2 − 5n − 6 = 0
n`= 6
n''=-1
Portanto
i=
180(6 − 2)
6
i = 120o
41)
x 1
=
y 3
180(x − 2)
3
x
=
180(y − 2) 5
y
y = 3x
(x − 2)
y
3
.
=
x
(y − 2) 5
(x − 2)
3x
3
.
=
x
(3x − 2) 5
3x 2 − 6x 3
=
3x 2 − 2x 5
3 x (x − 2) 3
=
x (3x − 2) 5
5(x − 2) = (3x − 2)
5x − 10 = 3x − 2
5x − 3x = 10 − 2
2x = 8
x=4
y = 3x = 3.4 = 12
y = 12
Logo,
x: quadrado
y: dodecágono
42)
a + b + c + d = 360o
x
3x
+ 2x +
+ x = 360o
2
2
x + 4x + 3x + 2x
= 360o
2
10x
= 360o
2
5x = 360o
x = 72o
Onde,
d = x = 72o
e = 90o
d + e + f = 180o
72o + 90o + f = 180o
f = 180o − 162o
f = 18o
43) A soma dos ângulos internos de um polígono é dado por (n-2)180. E caso este seja regular, a
(n − 2)180o
medida de cada ângulo é dado por
. No polígono regular, todos os ângulos internos são
n
iguais. Logo,
(n − 2)180o
= 160o
n
180n − 360 = 160n
180n − 160n = 360
20n = 360
360
n=
20
n = 18
Diagonal do polígono
n(n − 3) 18(18 − 3)
=
= 9.15
2
2
D = 135
D=
44)
T → 12 = x 2 + x 2
2x 2 = 1
x=
1 2
2
.
=
2 2
2
ABCDEFG = 1dm
Área PQRS = ?
2
2 2 2
+1+
=
+1 = 2 +1
2
2
2
Área do quadrado = . e os lados são iguais:
Área:
(
)(
2 +1
)
2 + 1 = 2. 2 + 2 + 2 + 1
Área: 2 + 2 2 + 1 = 3 + 2 2dm2
Resposta: A A = 3 + 2 2dm 2
45)
Si = 720o
razão = 20o
An = Ai + (n − 1)r
(n − 2)180 = 720
180n − 360 = 720
180n = 720 + 360
n=6
180(n − 2) 180(6 − 2)
Ai =
=
n
6
Ai = 150o
Ai + Ae = 180o
Ae = 180o − 150o
Ae = 30o
An = Ai + (n + 1)r
An = 30 + (6 − 1)20
An = 130o
Se a razão está para 20o 130o-20o=110o
46)
2
2
 11 − x   13 − x 
A⇒x =
 +

 2   2 
121 + x 2 − 22x 169 + x 2 − 26x
x2 =
+
4
4
2
4x 2 = 121 + x 2 − 22x + 169 + x 2 − 26x
4x 2 − 2x 2 − 48x − 290 = 0
2x 2 − 48x − 290 = 0
(÷2)
2
x − 24x − 145 = 0
x`=-29
x``=5
x=5
47)
0, 2
x`
0, 2
sen30o =
x`
1 0, 2
=
2 x`
x`= 0, 4 → CD
senθ =
Perímetro: AB+BC+CD+DE+EF+FG+GH+AH
P = 0, 4 + 1 + CD
+ 1 + 0,3 + 3,85
+ 1 + EF
T'
T ''
P=7,55+CD+EF
P=7,55+0,4+0,6
P=8,55m
48)
a) É um polígono regular com os oitos lados iguais e com seus ângulos internos e externos iguais.
b) Cálculo do ângulo central:
360
360
= 45o .
, onde n = 8 n
8
c) Si = (n-2)180°
Si = (8-2)180°
Si = 1080o
49) Polígonos estrelas são formados por cordas e ângulos em número iguais onde
α = β =γ =δ =ε = A
Se: α + β + γ + δ + ε = 5A = Si
5 ângulos iguais
5 cordas iguais (diagonais)
n(n − 3)
2
2
n − 3n
5=
2
2
n − 3n − 10 = 0
d=
n`= 5
n ``= −2
Portanto,
Sendo Si = a in e a i =
180(n − 2)
n
180(n − 2). n
n
5A = 180(5 − 2)
Si =
A = 108o
50)
n = n + 3

d = 3d
n(n − 3)
d=
2
(n + 3)(n + 3 − 3)
3d =
2
2
n + 3n
3d =
2
3n(n − 3) n 2 + 3n
=
2
2
3n 2 − 9n − n 2 − 3n = 0
2n 2 − 6n = 0
n 2 − 3n = 0
n(n − 3) = 0
n`= 0 → Não serve
n``= 3
n = n +3
n = 3+3 = 6
Si = 180(n − 2)
Si = 180(6 − 2)
Si = 180.4
Si = 720o
51) B
São formados 5 triângulos. Portanto, 5 x 180o = 900o .
52) 190
PG (360, 1080, 3240). Se n2 e n3 são os números de lados do segundo e terceiro polígonos
respectivamente, obtem-se que:
n(n − 3) 20(20 − 3)
=
= 170
2
2
n(n − 3) 8(8 − 3)
•d=
=
= 20
2
2
•d=
Total = 170 + 20 = 190 diagonais.
53)
Sint = 180o (n − 2) , com n = número de lados
2x+3x+4x+5x+6x=180.3
20x=540
x = 27
O menor ângulo é 2.27 = 54o
O complemento é o valor que falta para 90o: 90o – 54o = 36o
O maior desses ângulos é 6.x = 162o.
O suplemento é quanto falta para 180o: 180-162=18o.
Portanto,
Soma: 36 + 18 = 54o.
54) C
Visando x graus no sentido anti-horário (esquerda), a cada 4 metros, forma-se um ângulo de x, que deve
ser igual ao ângulo externo de um pentágono regular.
Portanto,
x=
360
= 72o
5
Nos passos I e II são construídos dois lados do pentágono. Portanto, é preciso executar o passo IV pelo
menos 3 vezes ou seja, y ≥ 3 .
Temos então, x.y ≥ 72.3 → xy ≥ 216
55) A
A soma dos ângulos internos desse polígono convexo é:
+B
+C
+D
+E
= 540o
A
2A + 2B + 2C + 2D + 2E = 1080o
2E + B = 360o
2A + C = 360o
2A + B + C + 360 + 360 = 1080
2A + B + C = 1080 − 360 − 360
2A + B + C = 360O
56)
θ = 30º + 60º = 90º .
57)
a = 100º
b = 110º
x=?
x + 80 + 70 = 180
x = 30º
58) B
40º + 2y = 180°
2y = 140
y = 70°
x + y + 40° = 180°
x + 70 + 40 = 180°
x = 180 – 110
x = 70°
59) A
=C
= 70° , pois ABC é isósceles,
Em ABC, B
logo y + z = 70°.
Em PBC, x + y + z = 180°
x + 70 = 180
x = 110°
60) C
x = 40° + 55°
x = 95°
61) B
I – Falsa
II – Verdadeiro. Se apenas um ângulo for igual, os
outros dois serão obtusos (maior que 90°), o que é
um absurdo, pois a soma dos ângulos internos
seria maior do que 180°.
III. Falsa
62) C
Os triângulos MCA e MBD têm dois lados
congruentes e que o ângulo compreendido entre
eles também é congruente. Logo, β = 84°
63) O Gabarito deve considerar o item B
Resolução: Os triângulos VWS e URT são equiláteros e assim possuem seus ângulos internos de 60°.
Soma dos ângulos internos = 180°
60° + 80° + α = 180°
α = 180° – 60° – 80°
α = 180° – 140°
α = 40°
64) C
a=x
a=4
b=3
c=4
b=3
c=x
a 2 = b 2 + c2
a 2 = b 2 + c2
x 2 = 32 + 42
4 2 = 32 + x 2
x 2 = 9 + 16
x 2 = 16 − 9
x 2 = 25
x2 = 7
x=5
x= 7
1 < x < 7 ou 5 < x < 7 .
65) B
XY = XZ
XP = PZ
PO = YO
b = 2a
a + 4a + 4a = 180°
9a = 180°
a = 20°
66) B
67)
180° = α + 30 + 180 − 60 − β
0 = α − β − 30
α − β = 30°
68)
a) o triângulo é acutângulo; ou seja todos os ângulos são < 90° (possuem 3 ângulos agudos).
69) C
C = 180° − z
(1)
C = 180° − y − 84º
(2)
180° − z = 180° − y − 84°
− z = − y − 84°
z = y + 84°
BC=BD
z + 2y = 180°
y + 84° + 2y = 180°
3y = 96
y = 32°
Portanto,
x + 32° + 48° + 48° = 180°
x = 180° − 128°
x = 52°
70) A
3k + 4k + 6k = 195
13k = 195
k = 15
O maior lado mede 6k = 6.15 = 90 metros
71) E
DC < AB + BC
73) B
2
m
H +   = (2m) 2
2
m2
H 2 = 4m 2 −
4
2
H = 4m 2 −
m2
4
16m 2 − m 2
15m 2
=
4
4
m
H=
15
2
m
m.
15
b.H
m2
2
Área =
=
=
15
2
2
2
H=