CINEMÁTICA ESCALAR Velocidade Escalar

CINEMÁTICA ESCALAR
A Física objetiva o estudo dos fenômenos físicos por meio de observação, medição e experimentação,
permite aos cientistas identificar os princípios e leis que regem estes fenômenos e fazer as
generalizações que são a base para invenções capazes de mudar o percurso da história da humanidade.
Neste ano estudaremos a Mecânica, que divide-se em dois tópicos:
Cinemática – Estudo dos movimentos; exploração de conceitos básicos como posição, velocidade e
aceleração.
Estática/Dinâmica – Análise do conceito de força e sua relação com o movimento; estudo de algumas
forças peculiares, até chegar ao conceito de trabalho e energia.
Ponto Material – No enunciado de temas e questões de física é comum a expressão ponto material: “... o
ponto material se desloca com v = 2 m/s...”.
Qual o significado dessa expressão? Qual a sua utilidade? A idéia física de ponto material é a de um
corpo cujas dimensões possam ser desprezadas em relação a outras dimensões envolvidas no
fenômeno que se esteja examinando.
Referencial – É o lugar onde está localizado de fato um observador em relação ao qual um dado
fenômeno (como um corpo em movimento) está sendo analisado. Por exemplo, quando o movimento é
analisado a partir de um referencial preso à Terra, imaginemos um observador ligado à ela e nos
transmitindo as imagens do fenômeno como ele o vê.
Movimento e repouso – Um corpo está em movimento em relação a um dado referencial quando as
sucessivas posições ocupadas pelo corpo, em relação a esse referencial, se modificam no decorrer do
tempo. Caso contrário, dizemos que o corpo está em repouso em relação a esse mesmo referencial.
Trajetória – Corresponde a linha geométrica descrita por um ponto material ao se deslocar em relação a
um dado referencial. A forma assumida pela trajetória depende do referencial adotado.
Espaço – representado pela letra s, é a medida algébrica, ao longo de uma determinada trajetória, da
distância do ponto onde se encontra o móvel ao ponto de referência adotado como origem.
Deslocamento Escalar – É a variação do espaço, representamos por Δs , dado pela diferença entre o
espaço final e o espaço inicial.
Velocidade Escalar
Imaginemos uma formiga em movimento e um homem andando sem correr. qual deles é o mais rápido?
Certamente o homem é o mais rápido, pois, num mesmo intervalo de tempo, o homem percorrerá uma
distância muito maior do que a percorrida pela formiga. Em vez de dizer que o homem é o mais rápido,
podemos dizer que a velocidade do homem é maior do que a velocidade da formiga.
A velocidade escalar média é a relação entre o deslocamento escalar Δ s e o correspondente intervalo de
tempo Δt
No Sistema Internacional (SI), a unidade de velocidade é metro por segundo (m/s). É também muito
comum o emprego da unidade quilômetro por hora (km/h). Pode-se demonstrar que 1 m/s é equivalente
a 3,6 km/h. Assim temos:
Movimento Progressivo – Acontece quando a velocidade escalar é positiva, significa que o móvel se
desloca a favor da orientação da trajetória.
Movimento Retrógrado – Acontece quando a velocidade escalar é negativa, significa que o móvel se
desloca contra a orientação da trajetória.
MOVIMENTO UNIFORME
Nas grandes cidades, devido ao intenso trânsito de veículos. é praticamente impossível manter
constante a velocidade de um carro. Mas, ao efetuarmos uma viagem, dependendo das condições da
rodovia, conseguimos manter o carro em velocidade constante durante um bom tempo. Quando isso
acontece, dizemos que o movimento do carro é uniforme.
O movimento de uma pessoa transportada numa escada rolante, o da Lua em torno da Terra e o dos
ponteiros de um relógio são exemplos de movimentos praticamente uniformes.
Função Horária
A função horária do espaço do movimento uniforme nos fornece o espaço de um móvel em qualquer
instante t≠0 , desde que sejam conhecidos o espaço inicial e a velocidade.
S = S0 + Vt
Exercícios:
1. Considere a seguinte situação: um ônibus movendo-se por uma estrada, e duas pessoas, uma, A,
sentada no ônibus, e outra, B, parada na estrada, ambas observando uma lâmpada fixa no teto do
ônibus.
A diz: “A lâmpada não se move em relação a mim.”
B diz: “A lâmpada está se movimentando, uma vez que ela está se afastando de mim.”
(a) A está errada e B está certa
(b) A está certa e B está errada
(c) Ambas estão erradas
(d) Cada uma, dentro do seu ponto de vista, está certa
2. A figura representa quatro posições (A, B, C e D) ocupadas por um móvel em um movimento
retilíneo.
a) Qual o espaço (posição) do móvel quando ele se encontra no ponto B? E quando se encontra no ponto
D?
b) Suponha que o móvel se desloque de A para C, determine o deslocamento e a distância percorrida.
c) Suponha, agora, que o móvel se desloque de B para D e, em seguida, retorne a C. Determine o
deslocamento entre B e C, e a distância percorrida neste deslocamento.
d) Suponha, agora, que o móvel se desloque de B para D e, em seguida, de D para A. Determine o
deslocamento entre B e A, e a distância percorrida neste deslocamento.
3. Um automóvel passou pelo km 24 de uma rodovia às 12 h. Em seguida, passou pelo km 208 da
mesma rodovia, às 14 h. Qual foi a velocidade média do automóvel entre os dois pontos, em km/h e em
m/s?
4. Transforme:
a) 36 km/h em m/s
b) 54 km /h em m/s
c) 30 m/s em km/h
d) 10 m/s em km/h
e) 20 m/s em km/h
5. As cidades de Vitória, no Espírito Santo, e Salvador, na Bahia, estão separadas por 1200km,
aproximadamente. Um automóvel sai de Vitória às 6 h, com destino a Salvador. Durante o trajeto o
motorista para por 1 h, para reabastecimento e lanche. Às 21 h ele chega a Salvador, tendo gasto na
viagem 104 litros de combustível. Determine:
a) Qual foi a velocidade média de toda a viagem?
b) Qual foi o consumo médio do combustível, em km/L?
6. Um atleta percorre 100 m em 10 s. Qual é a sua velocidade escalar média?
7. Uma pessoa percorre a pé 600 m em 10 min. Qual é a velocidade média dessa pessoa em m/s? E em
km/h?
8. Um automóvel passa pelo km 60 de uma rodovia às 10 h e pelo km 180 às 12 h. A velocidade escalar
média do automóvel entre esses dois pontos foi de:
(a) 120 km/h
(b) 90 km/h
(c) 60 km/h
(d) 30 km/h
(e) 13 km/h
9. Um ônibus parte às 8 h de uma cidade localizada no km 100 de uma rodovia e às 12 h para em um
posto localizado no km 400 dessa mesma rodovia para almoço. A velocidade média do ônibus nesse
trajeto foi de:
(a) 60 km/h
(b) 75 km/h
(c) 80 km/h
(d) 90 km/h
(e) 100 km/h
10. Um carro faz uma viagem de 400 km a uma velocidade média de 80 km/h. Um segundo carro,
partindo 1 h mais tarde, para chegar junto com o primeiro carro, deve movimentar-se a uma velocidade
média de:
(a) 66,7 km/h
(b) 80 km/h
(c) 90 km/h
(d) 100 km/h
(e) 120 km/h
11. Dois amigos fazem uma viagem de carro até uma praia, distante 800 km de sua cidade, em 10 h,
incluindo meia hora de parada para lanche e reabastecimento. A velocidade média do carro nessa
viagem foi de:
(a) 80 km/h
(b) 84 km/h
(c) 90 km/h
(d) 100 km/h
(e) 110 km/h
12. Qual é a velocidade média, em km/h, de uma pessoa que percorre, a pé, 1200 m em 20 min?
(a) 4,8
(b) 3,6
(c) 2,7
(d) 2,1
(e) 1,2
13. Um veículo vai do ponto A ao ponto B com velocidade média de 20 m/s e do ponto B ao ponto C com
velocidade média de 40 m/s. Calcule a velocidade média, em m/s, para todo o percurso.
14. Um observador O, situado em C vê passar uma carreta M dotada de velocidade constante 17 m/s;
4,2 segundos depois ouve o choque da carreta contra o obstáculo AB . Sendo de 340 m/s a velocidade
de propagação do som no ar, qual a distância, em metros, que separa o observador do obstáculo?
C
15. Os astrônomos costumam usar uma unidade de comprimento denominada ano-luz que é definida
como a distância percorrida pela luz, no vácuo, em 1 ano. Sabendo que a velocidade da luz no vácuo é
aproximadamente igual a 3 · 108m/s, o valor aproximado de 1 ano-luz é:
(a) 7,2 · 1012m
(b) 3,6 · 1012m
(c) 3,6 · 1015m
(d) 9,5 · 1015m
(e) 9,5 · 1012m
16. Os marinheiros costumam usar uma unidade de velocidade denominada nó. Por definição, 1 nó é
igual a 1 milha marítima por hora. Sabendo que 1 milha marítima é igual a 1852 metros, calcule o valor
aproximado, em km/h, da velocidade de um navio que se move com velocidade de 20 nós.
17. A velocidade máxima na BR-471, que corta a reserva do Taim, no Rio Grande do Sul, é de 60 km/h.
Essa velocidade corresponde a:
(a) 10 m/s
(b) 16,7 m/s
(c) 33,3 m/s
(d) 216 m/s
(e) 133 m/s
18. A distância média da Terra à Lua é de 390.000 km. Sendo a velocidade da luz no vácuo igual a
300.000 km/s, o tempo médio gasto por ela para percorrer essa distância é de:
(a) 0,77 s
(b) 1,3 s
(c) 13 s
(d) 77 s
(e) 1300 s
19. Um ônibus gastou 6 h para ir da Ponte do Rio Grande até são Paulo que distam aproximadamente
420 km. Percorreu, nas primeiras 3 h, 220 km e, nas 3 h seguintes, os 200 km restantes. É correto
afirmar que a velocidade média do ônibus foi de:
(a) 75 km/h
(b) 65 km/h
(c) 70 km/h
(d) 80 km/h
(e) 120 Km/h
20. Um carro movimenta-se com velocidade constante de 90 km/h. Quanto tempo ele demora para
alcançar um caminhão que está 500 m à frente e se desloca com velocidade de 54 km /h?
21. Em cada caso a seguir é dada a equação horária do espaço de uma partícula, no SI. Em cada caso,
determine o espaço inicial e a velocidade escalar e diga se o movimento é progressivo ou retrógrado.
a) s = 10 -2t
b) s = -8 + 3t
c) s = 4t
d) s = t + 20
22.Um automóvel que se desloca com velocidade constante de 72 km/h persegue outro que se desloca
com velocidade de 54 km/h, no mesmo sentido e na mesma estrada. O primeiro encontra-se 200 m
atrás do segundo no instante t = 0. O primeiro estará ao lado do segundo no instante:
(a) t = 10 s
(b) t = 20 s
(c) t = 30 s
(d) t = 40 s
(e) t = 50 s
23. Dois móveis, A e B, percorrem um trecho de estrada retilínea representado pelo eixo orientado. As
posições no instante inicial (t = 0) e os sentidos dos movimentos estão indicados na figura.
O instante de encontro é:
(a) 10 min
(b) 20 min
(c) 30 min
(d) 40 min
(e) 50 min
24. Você faz determinado percurso em 2,0 horas, de automóvel, se a sua velocidade média for 75 km/h.
Se você fizesse essa viagem a uma velocidade média de 100 km/h, você ganharia:
(a) 75 min
(b) 35 min
(c) 50 min
(d) 30 min
(e) 25 min
GABARITO:
1–D
2 – a) 25 m; 65 m
b) 30 m; 30 m
c) 15 m; 65 m
d) – 15 m; 95 m
3 – 92 Km/h; 25,56 m/s
4 – a) 20 m/s
b) 15 m/s
c) 108 Km/h
d) 36 Km/h
e) 72 Km/h
5 – a) 80 Km/h
b) 11,54 Km/L
6 – 10 m/s
7 – 1,0 m/s; 3,6 Km/h
8–C
9–B
10 – D
11 – A
12 – B
13 – 32 m/s
14 – 68 m
15 – D
16 – 37 Km/h
17 – B
18 – B
19 – C
20 – 50 s
21 – a) S0 = 10 m ; Vm = -2 m/s; RETRÓGRADO
b) S0 = - 8 m ; Vm = 3 m/s ; PROGRESSIVO
c) S0 = 0 m ; Vm = 4 m/s ; PROGRESSIVO
d) S0 = 20 m ; Vm = 1 m/s ; PROGRESSIVO
22 – D
23 – D
24 – D
Movimento Uniformemente Variado
Movimento uniformemente variado (MUV) é o movimento no qual a velocidade escalar varia uniformemente com o
tempo e a aceleração escalar é constante e diferente de zero (a ≠ 0). A aceleração escalar calculada em qualquer
instante é sempre a mesma para qualquer intervalo de tempo.
Vamos analisar agora o que acontece quando um carro está sendo freado.
Quando um carro está com uma velocidade de 20 m/s e freia até parar, como varia a sua velocidade?
Sua velocidade inicial pode diminuir a uma taxa de 5 m/s a cada segundo. Isto significa que em 1 s a sua velocidade
passa de 20,0 m/s para 15,0 m/s; decorrido mais 1 s a velocidade diminui para 10,0 m/s e assim sucessivamente até
parar.
Neste caso o movimento é uniformemente variado e é retardado, porque o valor absoluto da velocidade diminui no
decorrer do tempo (20,0 m/s, 15,0 m/s, 10,0 m/s, 5,0 m/s, 0,0 m/s).
A aceleração é constante e igual a - 5 m/s2 (o sinal negativo indica que o sentido da aceleração é oposto ao da
velocidade).
Se o valor absoluto da velocidade estivesse aumentando, o movimento seria acelerado, e neste caso, o sinal da
aceleração seria o mesmo da velocidade (o sentido da aceleração seria o mesmo da velocidade).
 Equações do MUV
a) Função Horária da Velocidade no MUV
Para obter a função (ou equação) da velocidade no movimento uniformemente variado, podemos partir do conceito de
aceleração escalar média, que diz:
A aceleração escalar média é a razão entre a variação da velocidade do móvel pelo intervalo de tempo gasto.
Matematicamente temos:
Fazendo t0 = 0, teremos:
E agora fazendo o produto do meio pelos extremos, teremos a função velocidade do movimento uniformemente
variado, veja:
V = V0 + at
Onde: V0 é a velocidade inicial do móvel e a é a aceleração.
b) Função Horária da Posição no MUV
A função horária da posição no MUV é:
Onde: S0 é a posição inicial, V0 é a velocidade inicial do móvel e a é a aceleração.
c) Equação de Torricelli
(V)2 = (V0)2+ 2 a ΔS
Onde: V é a velocidade final, V0 é a velocidade inicial do móvel, a é a aceleração e ΔS é o deslocamento.
 Gráficos do MUV
Podemos representar a função da velocidade, da posição e da aceleração do movimento uniformemente variado
através de gráficos.
a) Vxt: (velocidade em função do tempo dada pela equação V = V0 + at)
A função da velocidade é uma função do primeiro grau, sendo assim o gráfico é uma reta, que pode ser crescente ou
decrescente, dependendo do sinal da aceleração, positiva ou negativa. Veja:
b) axt: (aceleração em função do tempo)
A aceleração no MUV é constante e diferente de zero. Sendo assim, o seu gráfico é uma reta paralela ou eixo das
abscissas (eixo do tempo), veja:
Se a reta estiver acima do eixo a aceleração é positiva, do
contrário a aceleração é negativa.
c) Sxt: (posição em função do tempo dada pela equação
)
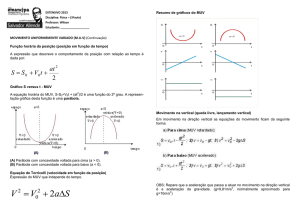
A função posição no MUV é uma função do segundo grau que pode ter concavidade para cima ou para baixo,
dependendo do sinal da aceleração, positivo ou negativo. Veja:
(A) Parábola com concavidade
voltada para cima (a > 0).
(B) Parábola com concavidade
voltada para baixo (a < 0).
E os vértices das parábolas indicam o instante que a velocidade é nula, isto só ocorre se inicialmente o sentido da
velocidade for oposto ao sentido da aceleração, isto é, inicialmente termos movimento retardado. Caso contrário, o
gráfico da parábola (Sxt) não terá vértice.
Exercícios:
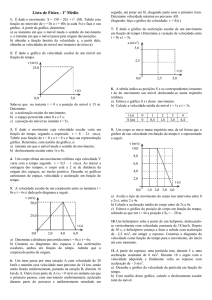
1. Um corpo, no instante de tempo t0 = 0 s, é lançado verticalmente para cima e alcança uma altura “H” num instante de
tempo “t”. Supondo nula a resistência do ar, identifique entre os gráficos abaixo, o que melhor representa a variação do
deslocamento do corpo, em função do tempo, desde “t0” até “t”. As curvas são ramos de parábola.
2. Um trem que possui 100 m de comprimento atinge a boca de um túnel e 30 s após, a extremidade de seu último
vagão abandona o túnel. Sabendo que a velocidade do trem é constante e igual a 20 m/s, podemos concluir que o
comprimento do túnel é:
(a) 4,5x102 m.
(b) 5,0x102 m.
(c) 6,0x102 m.
(d) 7,0x102 m.
(e) 7,5x102 m.
3. Um corpo, que se movimenta retilineamente, tem sua velocidade variando em função do tempo, conforme mostra o
gráfico abaixo.
Pode-se afirmar que aceleração que atuou neste corpo foi:
(a) maior no intervalo "C" do que no intervalo "A".
(b) nula no intervalo de tempo "B".
(c) nula no intervalo de tempo "D".
(d) variável nos intervalos de tempo "B" e "D".
(e) constante no intervalo de tempo "D".
4. Quando um corpo se movimenta retilineamente, sua velocidade varia de acordo com o tempo, conforme mostra a
seguinte tabela:
O Gráfico que melhor representa o comportamento da aceleração deste corpo em função do tempo é:
5. Um corpo de massa m movimenta-se sobre uma estrada retilínea, partindo de uma posição inicial -10m. O gráfico
representa a velocidade deste corpo em função do tempo.
A equação da velocidade que descreve este movimento é:
(a) V = 5 (-2 + t)
(b) V = 5 – 2,5 t
(c) V = -10 + 2,5 t
(d) V = 5 + t/2
(e) V = 5 (1 + t/2)
6. Lança-se um corpo para cima com uma velocidade inicial Vi e este leva um tempo t1 para atingir a altura máxima.
Pode-se afirmar, desprezando as forças de resistência do ar:
(a) Na metade da altura V = Vi/2
(b) Na metade da altura t = t1/2
(c) Para t = t1 a aceleração é zero.
(d) Para t = 2t1 o corpo estará no ponto de partida.
(e) Na metade da altura t = 3t1/2 .
7. Considere o gráfico posição (X) em função do tempo (t) para um móvel em movimento retilíneo. Qual é o gráfico
velocidade (V) em função do tempo (t) correspondente?
8. O gráfico em função do tempo mostra dois carros A e B em movimento retilíneo. Em t = 0s os carros estão na
mesma posição.
O instante em que os carros novamente se encontram na mesma posição é:
(a) 4,0 s
(b) 12,0 s
(c) 16,0 s
(d) 18,0 s
(e) 20 s
9. Um corpo é lançado de baixo para cima sobre um plano inclinado, livre de atrito, com velocidade inicial de 6,0 m/s.
Após 5/3 s ele atinge o topo do plano com velocidade de 1,0 m/s. A equação de velocidade que melhor se adapta a
este movimento é:
(a) V = 6 - 5t/3
(b) V = 5 - 5t/3
(c) V = 1 - 5t/3
(d) V = 6 - 3t
(e) V = 6 – t
10. Dois móveis, A e B, descrevem respectivamente um movimento retilíneo, representados pelo gráfico V x t abaixo.
A razão entre os deslocamentos dos móveis A e B durante os respectivos intervalos de tempo é:
(a) 5/6 (b) 3/20 (c) 1/2 (d) 1/15 (e) 4/30
11. Uma polia A de raio RA = 0,2 m está ligada, através de uma correia, a outra polia B de raio R B = 0,4 m sem
nenhum deslizamento entre as polias e a correia, durante o movimento.
Se o movimento descrito pelas polias A e B for movimento circular uniforme, então a velocidade angular da polia A é
numericamente:
(a)
(b)
(c)
(d)
(e)
igual à velocidade angular da polia B.
igual à velocidade tangencial da polia A .
a metade do que a velocidade angular da polia B.
ao dobro do que a velocidade angular da polia B.
a metade à velocidade tangencial da polia B.
12. Um móvel descreve um movimento retilíneo sob a ação de uma força constante, partindo da origem com
velocidade inicial nula e passando sucessivamente pelas posições X1 , X2 , X3 , X4 e X5 . O móvel gasta um intervalo
de tempo igual a 1/10 de segundo na passagem entre duas posições sucessivas.
Sendo constante a aceleração do móvel, podemos afirmar que esta aceleração vale, em m/s 2:
(a) 1
(b) 2
(c) 3
(d) 4
(e) 5
13. Uma esfera está deslizando sobre uma mesa sem atritos, com certa velocidade V0 . Quando a esfera abandona a
superfície da mesa, projetando-se no vácuo sob a ação da gravidade, descreve a trajetória representada na figura
abaixo.
A altura da mesa Y é de 5 m e o alcance horizontal
X é 10 m. Qual a velocidade inicial V0 da esfera, em
m/s?
(a) 2
(b) 4
(c) 5
(d) 8
(e) 10
Para responder às questões 14 e 15, utilize o gráfico v x t abaixo.
14. No intervalo de tempo compreendido entre t = 0s e t = 2s, a aceleração, em m/s2 é igual a:
(a) zero
(b) 2,0
(c) 3,5
(d) 4,0
(e) 5,0
15. Entre os instantes t = 4s e t = 8s, a distância percorrida pelo móvel, em metros, é de:
(a) 5,0
(b) 10
(c) 20
(d) 30
(e) 40
16. Qual dos gráficos abaixo representa a variação da velocidade V, em função do tempo t, de uma pedra lançada
verticalmente para cima? (A resistência do ar é desprezível.)
17. A posição inicial de um móvel que descreve um movimento retilíneo, representado pelo gráfico v = f(t) a seguir, vale
10 m.
A equação horária que melhor representa o movimento considerado é:
(a) S = 10 + 30t - 4t2
(b) S = 10 + 30t + 2t2
(c) S = 10 + 30t - 2t2
(d) S = 30t - 4t2
(e) S = 30t - 2t2
18. Dois automóveis, A e B, se deslocam sobre uma mesma estrada, na mesma direção e em sentidos opostos,
animados, respectivamente, das velocidades constantes VA = 90 km/h e VB = 60 km/h. Num determinado instante t0 =
0s , passam pelo mesmo ponto. Ao final de 15 min, contados a partir da passagem pelo referido ponto, a distância
entre os automóveis, em km, será:
(a) 10,0
(b) 37,5
(c) 42,7
(d) 54,8
(e) 81,3
GABARITO:
1–A
2–B
3–E
4–B
5–E
6–D
7–B
8–E
9–D
10 – B
11 – D
12 – E
13 – A
14 – E
15 – D
16 – E
17 – C
18 – B