Grafos - Inf

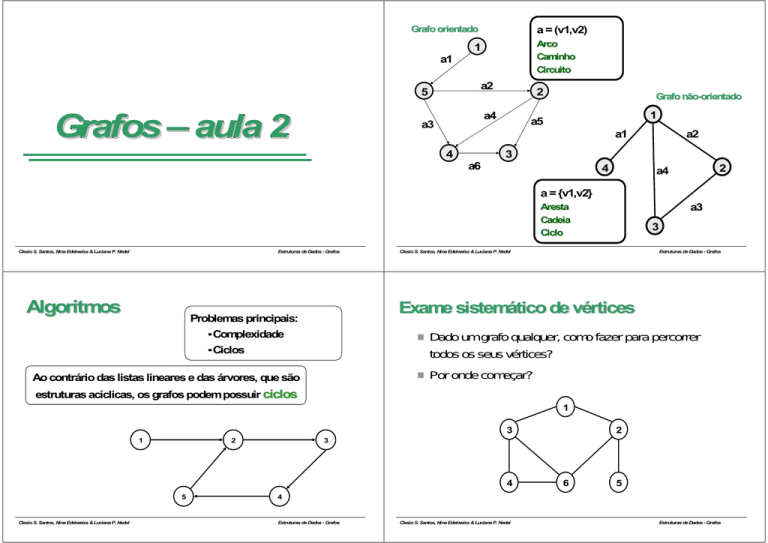
Grafo orientado
a = (v1,v2)
Arco
Caminho
Circuito
1
a1
5
Grafos – aula 2
a3
a2
2
a4
a5
Grafo nãonão-orientado
1
a1
4
a2
3
a6
4
2
a4
a = {v1,v2}
a3
Aresta
Cadeia
Ciclo
Clesio S. Santos, Nina Edelweiss & Luciana P. Nedel
Estruturas de Dados - Grafos
Algoritmos
3
Clesio S. Santos, Nina Edelweiss & Luciana P. Nedel
Estruturas de Dados - Grafos
Exame sistemático de vértices
Problemas principais:
• Complexidade
• Ciclos
„
„
Ao contrário das listas lineares e das árvores, que são
estruturas acíclicas, os grafos podem possuir ciclos
Dado um grafo qualquer, como fazer para percorrer
todos os seus vértices?
Por onde começar?
1
3
1
2
4
5
Clesio S. Santos, Nina Edelweiss & Luciana P. Nedel
2
3
6
5
4
Estruturas de Dados - Grafos
Clesio S. Santos, Nina Edelweiss & Luciana P. Nedel
Estruturas de Dados - Grafos
Exame sistemático de vértices
Exame sistemático de vértices
Percurso em profundidade
(Depth First Search)
1 1º
1
3
4
6
2
3 5º
5
4 6º
2 2º
6 4º
Clesio S. Santos, Nina Edelweiss & Luciana P. Nedel
5 3º
Estruturas de Dados - Grafos
1
3
3
1º
1
3º
4
2
2º
5
4º
2
4 6º
6
Clesio S. Santos, Nina Edelweiss & Luciana P. Nedel
Clesio S. Santos, Nina Edelweiss & Luciana P. Nedel
Estruturas de Dados - Grafos
Exame sistemático de vértices
Exame sistemático de vértices
Percurso em amplitude
(Breadth First Search)
Procedimento DFS (G: PGrafo; v: PVertice)
{ Exame em Profundidade (Depth First Search) }
{ visitado: atributo do nodo }
início
vÇ.visitado ← 1; { nodo v escolhido aleatoriamente }
para cada w adjacente a v
faça se wÇ.visitado = 0
então DFS(G,w);
fim; { DFS }
6
5º
5
Estruturas de Dados - Grafos
Procedimento BFS (G: PGrafo; v: PVertice)
{ Exame em Amplitude (Breadth First Search) }
{ visitado: atributo}
{ FV: Fila de vértices inicialmente vazia }
início
vÇ.visitado ← 1;
insere(FVÇ,v);
enquanto FV não vazia
faça início
v ← retira(FVÇ ); { retira primeiro elemento da fila }
para cada w adjacente a v
faça se wÇ.visitado = 0
então início
insere(FVÇ,w);
wÇ.visitado ← 1;
fim
fim
fim; { DFS }
Clesio S. Santos, Nina Edelweiss & Luciana P. Nedel
Estruturas de Dados - Grafos
Exercício
„
Escreva a ordem dos vértices percorridos pelos
caminhamentos em amplitude e profundidade para o
grafo abaixo:
1
2
7
3
4
8
Problema
„
„
Desejamos conectar todos os computadores em um
prédio de escritório usando a menor quantidade
possível de cabos
Como resolver o problema?
5
6
http://www.cs.duke.edu/csed/jawaa2/examples/DFS.html
http://www.cs.duke.edu/csed/jawaa2/examples/BFS.html
Clesio S. Santos, Nina Edelweiss & Luciana P. Nedel
Estruturas de Dados - Grafos
Árvore geradora de grafo
Clesio S. Santos, Nina Edelweiss & Luciana P. Nedel
Estruturas de Dados - Grafos
Algoritmo de Paton
Um grafo não-orientado G é uma árvore se satisfizer a
qualquer uma das seguintes condições:
G é conexo e sem ciclos;
G é conexo, com n vértices e n-1 arestas.
Uma árvore obtida pela remoção dos ciclos de
um grafo é chamada árvore geradora do
Objetivo: determinação de uma árvore geradora para um grafo
não-valorado
A – arestas de G
V – vértices de G
AA – arestas da árvore geradora
VA – vértices da árvore geradora
X vértices ainda não examinados
grafo.
Clesio S. Santos, Nina Edelweiss & Luciana P. Nedel
Estruturas de Dados - Grafos
Clesio S. Santos, Nina Edelweiss & Luciana P. Nedel
Estruturas de Dados - Grafos
Árvore geradora de grafo
Algoritmo de Paton
6
6
Objetivo: determinação de uma árvore geradora para um grafo
não-valorado
1
AA = 0; VA = 0; X = V;
1. Escolhe um vértice de V para raiz da árvore
2. Visita os vértices adjacentes a raiz
3. Repete-se mesmo procedimento para o último vértice
visitado
1
5
G
2
A1
2
4
Estruturas de Dados - Grafos
Algoritmo de Paton
A
3
6
1
5
2
4
3
Clesio S. Santos, Nina Edelweiss & Luciana P. Nedel
Estruturas de Dados - Grafos
Árvore geradora mínima
D
19
B
4
3
A2
Clesio S. Santos, Nina Edelweiss & Luciana P. Nedel
5
1
1
9
9
C
6
17
E
6
8
23
30
30
4
27
2
7
17
15
8
5
2
7
3
5
23
4
3
27
Árvore geradora mínima é, dentre as árvores
geradoras, aquela que apresenta a menor soma dos valores
associados às linhas.
Clesio S. Santos, Nina Edelweiss & Luciana P. Nedel
Estruturas de Dados - Grafos
Clesio S. Santos, Nina Edelweiss & Luciana P. Nedel
Estruturas de Dados - Grafos
Algoritmo de Kruskal
Algoritmo de Kruskal
Objetivo: determinação de uma árvore geradora para um grafo
valorado
1. Iniciar com os n vértices e nenhuma aresta
2. Fila ordenada dos arestas
3. Acrescentar uma aresta ainda não colocada e que não
fecha ciclo
4. Repetir o passo 3 até que n-1 arestas tenham sido
colocadas
Geração de árvore geradora mínima:
escolhendo sempre os menores
valores de arcos disponíveis
O algoritmo exige que se tenha um método para determinar se
uma aresta fecha ciclo ou não.
–http://students.ceid.upatras.gr/~papagel/project/kruskal.htm
Clesio S. Santos, Nina Edelweiss & Luciana P. Nedel
Estruturas de Dados - Grafos
Algoritmo de Kruskal
Clesio S. Santos, Nina Edelweiss & Luciana P. Nedel
Algoritmo de Kruskal
Algoritmo Kruskal (G);
G: Grafo não-orientado, sem laços, com n vértices v1 ... vn e m arestas a1={u1,w1} ..... am={um,wm}
A: Árvore de cobertura mínima
19
1
6
Estruturas de Dados - Grafos
2
7
6
4
Clesio S. Santos, Nina Edelweiss & Luciana P. Nedel
27
3
2
7
8
23
30
9
17
15
8
5
1
9
17
para cada vértice v em G faça
Defina um grupo elementar C(v) := {v} { um grupo é uma lista não ordenada de vértices }
Inicialize uma fila ordenada Q para conter todas as arestas em G,
usando seus pesos como chaves
1
19
9
Inicializa A
enquanto A tem menos de n-1 arestas faça
6
2
7
RetiraFila(u,v);
17
15
Seja C(v) o grupo contendo v e C(u) o grupo contendo u
8
23
se C(v) <> C(u) então
5
4
3
Coloque aresta (v,u) em A
30
27
Unifique C(v) e C(u) em um grupo
Retorna a árvore A
Clesio S. Santos, Nina Edelweiss & Luciana P. Nedel
Estruturas de Dados - Grafos
5
23
4
3
Estruturas de Dados - Grafos
Exercício
„
„
„
„
Existem 8 pequenas ilhas em um
arquipélago e o governo deseja
construir 7 pontes conectando-as
de forma que cada ilha possa ser
alcançada de qualquer outra ilha
através de uma ou mais pontes
O custo de construção de uma
ponte é proporcional ao seu
comprimento
As distâncias entre os pares de
ilhas são dados na tabela abaixo
Ache quais pontes devem ser
construídas para que o custo da
construção seja mínimo
Clesio S. Santos, Nina Edelweiss & Luciana P. Nedel
1
2
3
4
5
6
7
8
1
-
240
210
340
280
200
345
120
2
-
-
265
175
215
180
185
155
3
-
-
-
260
115
350
435
195
4
-
-
-
-
160
330
295
230
5
-
-
-
-
-
360
400
170
6
-
-
-
-
-
-
175
205
7
-
-
-
-
-
-
-
305
8
-
-
-
-
-
-
-
-
Estruturas de Dados - Grafos