Prova com Gabarito Engenharia Fisica CAT

UNIVERSIDADE FEDERAL DE ITAJUBÁ
CÁLCULO 1 e 2 – PROVA DE TRANSFERÊNCIA INTERNA, EXTERNA E PARA
PORTADOR DE DIPLOMA DE CURSO SUPERIOR 01/12/2013
CANDIDATO: _____________________________________________________
CURSO PRETENDIDO: _______________________________________________
OBSERVAÇÕES:
01 – Prova SEM consulta.
02 – A prova PODE ser feita a lápis.
03 – PROIBIDO o uso de calculadoras e similares.
04 – Duração: 2 HORAS.
1a Questão (10 pontos): Sabe-se que o ponto P2,7  é o ponto de maior ordenada do gráfico da
função definida por f x   ax 2  8bx  1 . Nestas condições, o valor de f 3 é:
a) 5
b) 6
c) 7
d) 8
e) 9
SOLUÇÃO
Como a função é quadrática e possui um valor máximo, então a  0 .
O ponto P2,7  é o vértice da parábola f x   ax 2  8bx  1 .
Assim: xV  2  
yV  7  
8b
a
2  b
2a
2
(1)

4ac  b 2
 4a  64b 2
16b 2
7 
7 
 7  1
 7 (2)
4a
4a
4a
a
Substituindo (1) em (2):  1 
16 a 2
.
 7   1  4a  7  a  2
a 4
a
Como b   , então b  1 .
2
Portanto, a função quadrática é: f x   2 x 2  8x  1
Para x  3 , teremos: f 3  2.32  8.3  1 
f 3  5
2a Questão (10 pontos): Sabendo que a função f x   x 3  2 x 2  ax  b apresenta um máximo
relativo no ponto P 1,6 , concluímos que o valor de 3b  2a  é igual a:
a) 12
b) 13
c) 14
d) 15
e) 16
SOLUÇÃO
Como a função possui máximo relativo no ponto P 1,6 , então neste ponto devemos ter a
derivada igual a zero, ou seja, f  1  0 .
Como f x   3x 2  4 x  a , então 3. 1  4. 1  a  0  3  4  a  0  a  1 .
2
Como o ponto P 1,6 pertence à curva, então devemos ter f  1  6 .
Assim: 6  1  2  1  b  b  6 .
Portanto: 3b  2a  16
3a Questão (10 pontos): Se z  f x, y  ;
z 1
  ye xy  2 x e
x x
f 1, y   ln y  e y  2 y , quanto vale
f 1,1 ?
a) e
b) e  1
c) e  2
d) e  3
SOLUÇÃO
Temos: f x, y   
z
1

dx  f x, y      ye xy  2 x  dx
x
x

Calculando: f x, y   ln x  e xy  x 2  C  y 
Para x  1 
f 1, y   ln 1  e y  12  C  y 
ln y  e y  2 y  0  e y  1  C y   C y   ln y  2 y  1
Portanto: f x, y   ln x  e xy  x 2  ln y  2 y  1
Logo: f 1,1  ln 1  e  1  ln 1  2  1 
f 1,1  e  2
e) e  4
4a Questão (10 pontos): O valor da integral I  
a)
b) 2 2
2
dt
8
1 3
c) 3 2
é:
t. 1 3 t
d) 4 2
e) 5 2
SOLUÇÃO
Fazendo: 1  3 t  x 
3


Para t  1  x  2

Para t  8  x  3
Assim: I  


2
3. x 2  1 .2 x.dx
 I 
2
x. x 2  1
3


 x3

Calculando: I  6.  x 
3


t  x2 1  t  x2 1
3
2

3
151
3
b)
152
3
3
 I 2 2
2
c)
154
3
4
I 
0
2  64
 x3


  xy  dy  I   0   4 y  dy
 3

3
0
2
2

d)
SOLUÇÃO
2

6. x 2  1 .dx
5a Questão (10 pontos): Calculando o valor da integral
a)

 dt  3. x 2  1 .2 x.dx .
128
152
 64

I   y  2y2 
 I
8  I 
3
3
3
0
  x
2
4
0
0
155
3
2

 y dxdy , obtemos:
e)
157
3
6a Questão (10 pontos): Resolver a integral I   x  5 .2 x  3dx , usando o Método de
9
Integração Por Partes  udv  u.v   vdu .
SOLUÇÃO
u  2 x  3  du  2dx

10
Fazendo: 

x  5 .
9
dv  x  5 dx  v 
10

Assim: I  2 x  3.
x  510  x  510 .2dx .
10

2 x  3x  5
I

10

10
10
2  x  5
.
C
10
11
11
10

x  5 
2x  5 
I
. 2x  3 
C
10
Finalmente:




11

10

x  5 22 x  33  2 x  10
I
.
C.
10
11
10

x  5 .20 x  43
I
C
110
7a Questão (10 pontos): Calcular a área limitada pela parábola y 2  4 x e pela reta y  2 x  4 .
SOLUÇÃO
A parábola y 2  4 x tem o vértice na origem e a concavidade voltada para a direita e a reta
y  2 x  4 é oblíqua aos eixos coordenados.
y
y  2x  4
4
x*
y
0
2
4
2
x
y 2  4x
Como a área a ser calculada situa-se toda à direita do eixo y , é conveniente escolher um
retângulo elementar da forma x * .y , onde x *  xreta  x parábola.
Por outro lado, para identificarmos os limites de integração, é necessário encontrar os pontos
de interseção da reta e da parábola.
Assim, obtivemos os pontos y  2 e y  4 .
Portanto: S  
4
2
y
y2
x .dy , onde x   2 
2
4
*
*
4
y
 y2
y2 
y3 
16 2
Logo: S     2  .dy    2 y    4  1  8  4  

2 2
4
12  2
3 3

4
4
8a Questão (10 pontos): Resolver a integral I  


ex. ex  2
dx , usando uma substituição de
e2x  4
variáveis conveniente.
SOLUÇÃO
Fazendo: e x  t  e x .dx  dt .
Assim: I  
I
t2
t
2
dt  I   2
dt   2
dt
2
t 4
t 4
t 4


1
2t
1
1
t
dt  2 2
dt  I  ln t 2  4  arctg    C
2
2

2 t 4
2
t 2
2
Como e x  t , então I 
 ex
1
ln e 2 x  4  arctg 
2
 2



  C

S  9 u. A.
9a Questão (10 pontos): Usando Frações Parciais, resolver a integral I  
8
dx .
x  4x
3
SOLUÇÃO
I 
8
8
dx  
dx
2
x  4x
x. x  4
3

Por Frações Parciais:


8
x. x  4
2


A Bx  C
.

x x2  4
8  Ax 2  4  Bx  C .x  8   A  Bx 2  Cx  4 A
 A  B  0  B  2

Comparando: C  0
4 A  8  A  2

2
 2x
Assim: I   dx   2
dx  I  2 ln x  ln x 2  4  C
x
x 4


10a Questão (10 pontos): Determinar os pontos de Máximo Relativo, Mínimo Relativo ou de Sela
da função f x, y   x3  y3  3x  12 y  20
2 z
 AC  B , onde A  2
DADO: Hessiano:  
B C
x P
A B
2
;
SOLUÇÃO
I 
8
8
dx  
dx
2
x  4x
x. x  4
3

Por Frações Parciais:


8
x. x  4
2


A Bx  C

.
x x2  4
8  Ax 2  4  Bx  C .x  8   A  Bx 2  Cx  4 A
 A  B  0  B  2

Comparando: C  0
4 A  8  A  2

2
 2x
dx  I  2 ln x  ln x 2  4  C
Assim: I   dx   2
x
x 4
2 z
B
yx P
2 z
; C 2 .
y P
UNIVERSIDADE FEDERAL DE ITAJUBÁ
GABARITO DE FÍSICA – PROVA DE TRANSFERÊNCIA INTERNA, EXTERNA E
PARA PORTADOR DE DIPLOMA DE CURSO SUPERIOR 01/12/2013
CANDIDATO: _____________________________________________________
CURSO PRETENDIDO: _______________________________________________
OBSERVAÇÕES:
01 – Prova SEM consulta.
02 – A prova PODE ser feita a lápis.
03 – PROIBIDO o uso de calculadoras e similares.
04 – Duração: 2 HORAS.
1a Questão: Duas esferas de aço descrevem um movimento retilíneo uniforme sobre uma mesa
horizontal. A velocidade da esfera A é o dobro da velocidade da esfera B e ambas chegam à
borda da mesa no instante t = 0. Considere que t A seja o instante em que a esfera A toca o solo e
que tB seja o instante em que a esfera B toca o solo. Supondo que a massa das esferas seja igual
e que a resistência do ar possa ser desprezada, é correto afirmar que:
a.
b.
c.
d.
e.
tA = (1/4) tB.
tA = (1/2) tB.
tA = tB.
tA = 2 t B .
tA = 4 t B .
Solução: Alternativa (c). O movimento horizontal e o vertical são independentes. As duas esferas
têm a mesma velocidade vertical (vy = 0) e começam a cair da mesma altura. Portanto ambas
levarão o mesmo tempo para chegar ao solo.
2a Questão: Um automóvel percorre com velocidade escalar constante uma curva horizontal que
tem a forma de um arco de circunferência. A força resultante sobre esse automóvel é devida:
a.
b.
c.
d.
e.
à atração gravitacional que a Terra exerce sobre o automóvel.
à reação normal que a pista exerce sobre o automóvel.
ao atrito entre a pista e o automóvel.
ao motor do automóvel.
ao ar.
Solução: Alternativa (c). Como a velocidade escalar é constante, o movimento é circular e
uniforme. Logo a aceleração do automóvel é a aceleração centrípeta. Como a curva é horizontal, a
única força que tem um componente que aponta para o centro da trajetória é a força de atrito.
3a Questão: Um objeto puntiforme realiza um movimento
retilíneo cujo gráfico posição versus tempo é mostrado na
figura ao lado. Assinale a afirmativa correta:
a.
b.
c.
d.
O objeto se move com velocidade constante.
O objeto está acelerando o tempo todo.
O objeto está freando o tempo todo.
O objeto está acelerando em uma parte do
movimento e freando em outra parte.
e. O objeto se move com aceleração nula.
Solução: Alternativa (b). Em um gráfico posição versus tempo a velocidade em um ponto é
numericamente igual ao valor da tangente à curva naquele ponto. No gráfico em questão pode ser
visto que a magnitude da velocidade é zero no instante inicial e aumenta à medida que o tempo
passa. Portanto o objeto está acelerando o tempo todo.
4a Questão: ANULADA
(A pontuação referente a esta questão será atribuída a todos os candidatos que compareceram à prova).
5a Questão: No pêndulo cônico da questão anterior, o momento angular da esfera em relação ao
ponto O é:
a.
b.
c.
d.
e.
tangente à circunferência descrita pela esfera.
paralelo ao eixo z.
perpendicular ao eixo z.
paralelo ao fio.
perpendicular ao fio.
Solução: Alternativa (b). O momento angular L é dado pelo produto vetorial L = r x p (r é o vetor
posição da esfera em um determinado instante e p é seu momento linear). Como r tem a direção
radial e p = m v é tangente à circunferência, L será paralelo ao eixo z.
6a Questão: Um projétil de 100 g com uma velocidade de 500 m/s colide com um paralelepípedo
maciço de 900 g, inicialmente em repouso sobre uma superfície horizontal sem atrito. Supondo
que a velocidade do projétil imediatamente antes da colisão seja horizontal e que ele fique
encravado no paralelepípedo, calcule a energia cinética do conjunto formado pelos dois corpos
logo após a colisão.
Solução:
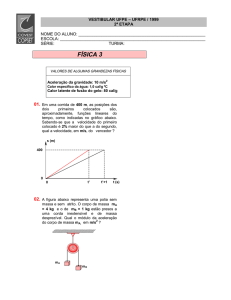
7a Questão: A figura ao lado mostra dois blocos, A e B, ligados por um
fio inextensível de massa desprezível que passa por uma roldana de
massa 2,0 kg e raio 0,10 m. O sistema está inicialmente em repouso e o
bloco B está apoiado no solo. Considerando mA = 3,0 kg e mB = 1,0 kg,
quando o sistema é solto, o bloco A desce e o bloco B sobe. A partir
dessas informações, calcule a aceleração angular da roldana enquanto o
bloco A estiver descendo.
Dados: g = 10 m/s2; Iroldana = (1/2) m r2.
Solução:
8a Questão: Uma partícula descreve um movimento unidimensional sob a ação de uma única
força que é expressa no Sistema Internacional de unidades (SI) por F (x) = k x 2. Nesta expressão,
k = 6,00 N.m-2 é uma constante. Calcule o trabalho devido a essa força quando a partícula se
desloca entre as posições x1 = 3,00 m e x2 = 5,00 m.
Solução:
9a Questão: Uma plataforma gira sem atrito com velocidade angular de 6,0 rad/s. No centro dessa
plataforma encontra-se uma pessoa de pé com os braços abertos segurando um par de halteres
em cada mão. Nesta situação o momento de inércia do conjunto é de 12 kg m 2, mas quando a
pessoa encolhe os braços, o momento de inércia cai para 8,0 kg m2. Calcule a velocidade angular
do conjunto após a pessoa ter encolhido os braços.
Solução:
10a Questão: Uma partícula de 3,0 kg, inicialmente em repouso, está sujeita a uma única força F.
Essa força varia em função do tempo como mostra a figura. A partir dessas informações, calcule a
magnitude do impulso devido a essa força.
Solução: