Movimento de um Projétil

6º Trabalho Prático – Física I
Movimento de um Projétil
I - Introdução

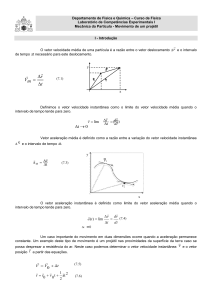
O vetor velocidade média de uma partícula é a razão entre o vetor deslocamento  r
e o intervalo de tempo t necessário para este deslocamento.
y

Vm 

r
r
(7.1)
r0
t
r
x
Definimos o vetor velocidade instantânea como o limite do vetor velocidade média
quando o intervalo de tempo tende para zero.


r  dr
t
dt

v  lim
t  0
(7.2)
 Vetor aceleração média é definido como a razão entre a variação do vetor velocidade
v
instantânea  e o intervalo de tempo t.


v
aM  
t
y
v1
(7.3)
v2
x
O vetor aceleração instantânea é definido como limite do vetor aceleração média
quando o intervalo de tempo tende para zero.


v dv

a (t )  lim

t
dt
t
(7.4)
0
Um caso importante do movimento em duas dimensões ocorre quando a aceleração
permanece constante. Um exemplo deste tipo de movimento é um projétil nas proximidades da
superfície da terra caso se possa desprezar a resistência do ar. Neste caso podemos determinar o
vetor velocidade instantânea


v e o vetor posição r a partir das equações.
10



V  V0  at
(7.5)
1
 

r  r0  v 0 t  at 2
2
(7.6)
y
y
½ at2
½ ayt2
a yt
Vy
y
V0y
V0
V
V0x
axt
v0t
v0yt
y0
r0
x
Vx
x0
v0xt
½ axt2
x
x
As componentes x e y das equações (7.5) e (7.6) são
Vx = V0x + axt
X = X0  V0xt + ½ axt
(7.7)
Vy = V0y + ayt
Y = Y0  V0yt + ½ ayt
(7.8)
Podemos aplicar estes resultados ao movimento de um projétil. Desprezando a
resistência do ar a aceleração do projétil é aceleração da gravidade g . A aceleração da gravidade
próxima à superfície da terra é aproximadamente igual a 9,8 m/s2 e verticalmente para baixo.
Logo a aceleração do projétil ax = 0 e ay = -g.
Temos:
Vx = V0x = V0 cos 
(7.9)
X = X0 + Voxt = X0 + (V0 cos ) .t
Vy = V0y - gt = (V0 sen) - gt
Y = Y0 + V0yt - ½
gt2
(7.10)
= Y0 + (V0 sen ).t - ½ gt2
Vamos estudar uma situação onde X0 = 0 e  = 0. Neste caso as componentes X e Y
poderão ser escritas como:
11
x  v0t
(7.11)
1
y  y 0  gt 2 (7.12)
2
gx 2
y  y0 
(7.13)
2 v 02
O alcance
R do projétil poderá ser obtido a partir da equação (7.13), Fazendo Y = 0
R  v0
2y 0
g
(7.14)
II - Desenvolvimento
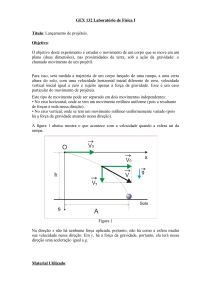
O objetivo deste trabalho é comparar as características dos movimentos ao longo dos
dois eixos, ou seja, verificar se o movimento do projétil é descrito pelas equações (7.7) e (7.8). Você
dispõe em sua mesa de uma montagem que consiste se uma rampa inclinada e um anteparo. A
rampa foi montada de modo que uma bolinha abandonada a uma altura h em relação à mesa, deixa a
rampa com velocidade horizontal Vo.
Variando a distância, X, do anteparo à base da rampa, meça o tempo de movimento
de bolinha, a partir do momento em que deixa a rampa até chocar com o anteparo.
Anote também os valores da coordenada Y do ponto em que a bolinha atinge o
anteparo.
Resolva as questões seguintes:
1. Construa os gráficos X x t, Y x t, Y x X.
2. Use a regressão linear para encontrar a velocidade inicial da bolinha.
3. Os gráficos obtidos estão de acordo com as equações (7.11), (7.12) e (7.13) ? Quais as fontes de
erro ?
4. Usando a equação (7.14) determine a aceleração da gravidade.
12