Argumento

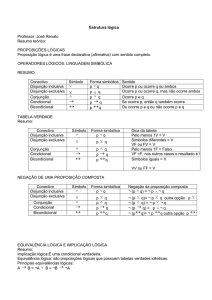
Argumentação Com Conectivos
É toda sequência finita de proposições (premissas)
que tem como resultado uma conclusão.
Representação de um argumento:
P1 ; P2 ; P3 ; P4 ; ...........PN │―
C
Silogismo
É todo argumento que tem como estrutura,
somente, duas premissas e uma conclusão.
Por exemplo:
•Hoje é sábado ou domingo.
•Hoje não é sábado.
•Logo, hoje é domingo.
Representação de Silogismo
P1 ; P2 │― C ou P1
P2
.................
C
Validade de um Argumento
“A verdade das premissas é incompatível com a
falsidade da conclusão, ou seja, duas premissas
verdadeiras
devem
conclusão verdadeira”.
sempre
garantir
uma
Argumento Válido ou Bem Construído:
P1
P2
C
V
V
V
Argumento Não Válido, Mal Construído, Sofisma ou Falácia:
P1
P2
C
V
V
F
Exemplo:
Considere como verdadeiras as seguintes premissas:
I. Se Alfeu não arquivar os processos, então Benito fará a expedição de documentos;
II. Se Alfeu arquivar os processos, então Carminha não atenderá o público;
III. Carminha atenderá o público.
Logo, é correto concluir que:
a) Alfeu arquivará os processos;
b) Alfeu arquivará os processos ou Carminha não atenderá o público;
c) Benito fará a expedição de documentos;
d) Alfeu arquivará os processos e Carminha atenderá o público;
e) Alfeu não arquivará os processos e Benito não fará a expedição de documentos.
Solução:
Considerando como verdadeiras as premissas:
I. Se Alfeu não arquivar os processos, então Benito fará a
expedição de documentos: ( p  q ) = V
II. Se Alfeu arquivar os processos, então Carminha não
atenderá o público: ( ~p  r ) = V
III. Carminha atenderá o público: ( r ) = V
Argumento:
P1: (p  q) = V ----- p = V e q = V
P2: (~p  r) = V ---- r = F e ~p = F
C: (~r) = V
Logo, é correto concluir que:
a) Alfeu arquivará os processos;
b) Alfeu arquivará os processos ou Carminha não
atenderá o público;
c) Benito fará a expedição de documentos;
d) Alfeu arquivará os processos e Carminha
atenderá o público;
e) Alfeu não arquivará os processos e Benito não
fará a expedição de documentos.
Exemplo:
Considere a seguinte sequência de proposições:
I. Se o crime foi perfeito, então o criminoso não foi preso;
II. O criminoso não foi preso;
III. Portanto, o crime foi perfeito.
Se (1) e (2) são premissas verdadeiras, então a proposição (3),
a conclusão, é verdadeira; e a sequência é uma dedução lógica
correta. Item certo ou errado?
Considerando a sequência de proposições:
I. Se o crime foi perfeito, então o criminoso não foi preso: (p  q)
II. O criminoso não foi preso: (q)
III. Portanto, o crime foi perfeito: (p)
Se (1) e (2) são premissas verdadeiras, então a proposição (3), a
conclusão, é verdadeira, e a sequência é uma dedução lógica
correta.
Considerando a sequência de proposições:
P1. ( p  q) = V ---- ( p  V ) = V ; p = ?
P2. ( q ) = V
P3 = C. ( p ) = ?
Assim, não temos como deduzir o valor lógico de p. Então,
o argumento não é consistente, deixa dúvida.
Item errado