LINEARIZAÇÃO DOS PARÂMETROS DE SENSIBILIDADE TENSÃO

LINEARIZAÇÃO DOS PARÂMETROS DE SENSIBILIDADE TENSÃO x
TENSÃO E TENSÃO x CARREGAMENTO PARA REGULAÇÃO REMOTA EM
ALIMENTADORES DE MÉDIA TENSÃO
MANOEL FIRMINO DE MEDEIROS JR.*,JOSÉ ALBERTO NICOLAU DE OLIVEIRA+, MAX C. PIMENTEL FILHO+
*
Departamento de Eng. de Computação e Automação, +Programa de Pós-gradução em Eng. Elétrica, Univ. Fed. do
Rio G. do Norte - UFRN
C.E.P. 59072-970 Natal, RN, BRAZIL
E-mails: [email protected], [email protected], [email protected]
Abstract – This paper describes firstly an algorithm to
calculate sensitivity parameters for evaluating the
dependence between voltages in radial distribution systems,
as well between voltages and network loading. Secondly,
linearization hypothesis of these parameters based on
results of exaustive load flow calculations are presented.
The aim of linearization is to reduce computer efforts in
order to allow an embedded algorithm for local or remote
voltage regulation.
Keywords – Distribution networks, voltage regulation,
sensitivity parameters, linearization.
I. INTRODUÇÃO
O cálculo de fluxo de carga em redes de distribuição tem
como um de seus objetivos, determinar as tensões nodais,
para uma condição fixa de carregamento. Se ocorrer uma
mudança no seu carregamento e/ou houver uma variação da
tensão em algum ponto, em virtude da atuação de um
regulador de tensão, para se conhecer as novas tensões do
sistema, um novo cálculo de fluxo de carga deverá ser
executado. Todavia, com o conhecimento de parâmetros de
sensibilidade [1], tais como as derivadas parciais do módulo
da tensão em um nó, com relação ao fator de carregamento,
ou à tensão em um outro nó, é possível realizar uma
estimativa, através de uma linearização, de mudanças
ocorridas no perfil de tensão, em decorrência de variações
impostas a parâmetros de controle como taps de
transformadores ou reguladores de tensão [2], como também
a variações no carregamento. Este trabalho apresenta a
dedução dessas derivadas parciais, bem como simulações que
justificam a sua constância, para a região de interesse. O
objetivo consiste em, através de um único cálculo de fluxo de
carga, determinar o perfil de tensão do sistema para vários
níveis de carregamento, como também após da atuação de
um regulador de tensão.
Adotou-se neste trabalho, para o cálculo dessas derivadas,
as equações do método da soma de potências [3] em sua
versão monofásica, que foi desenvolvido procurando
explorar as características de sistemas radiais de energia
elétrica. O cálculo de fluxo de carga, entretanto, foi
realizado através do algoritmo trifásico apresentado em [4].
II. DERIVADA DO MÓDULO DA TENSÃO EM UM NÓ
COM RELAÇÃO AO MÓDULO DA TENSÃO EM UM
OUTRO NÓ
De acordo com o método da soma de potências o cálculo da
tensão em um nó é feito utilizando a equação bi-quadrada:
Rk 2 + X k 2
2(Rk
Psk 2 + QSk 2 +
Psk + X k
Onde:
P k , Qk
Pski,Qsk
sistema no nó k;
Vj
Rk, Xk
Qsk )
Vi 2 Vk 2 + Vk 4 = 0
(1)
= Cargas ativa e reativa líquidas no nó k;
= Cargas ativa e reativa equivalentes do
= Módulo da tensão no nó j;
= Resistência e reatância da linha índice k;
LP k
LQ k
= Perda ativa na linha k;
Lk
= Perda complexa na linha k;
= Balanço de reativo na linha k;
I *k
= Conjugado da corrente no trecho k;
j
i
k
Isolando Vk :
= Índice;
= Nó do lado da fonte;
= Nó do lado da carga.
Vk =
Onde:
− B + B2 − 4 ⋅ A ⋅ C
2⋅ A
(2)
A=1
B = 2 Rk ⋅ Psk + X k Qsk − Vi2
(
)(
C = Rk2 + X k2 Psk2 + Qsk2
Portanto:
)
(3)
∂Vk
∂V j
−
=
1 −B+
⋅
2
∂B
∂V j
B2 − 4 ⋅ A ⋅ C
−
1
2
∂V k
2⋅ A
∂Fc
(
)
1
−
∂B
∂C
1
+ ⋅ B2 − 4 ⋅ A ⋅ C 2 ⋅ 2 ⋅ B ⋅
−4⋅
2
∂V
∂V
j
−
j
=
1 −B+
⋅
2
∂B
∂Fc
(4)
Observando a equação da derivada, pode-se notar que a
derivada de Vk depende da derivada de Vi , que é a tensão no
nó anterior, tornando parecer impossível o cálculo dessa
derivada. Entretanto, considerando que o sistema é radial, se
o cálculo da derivada for iniciado, partindo do nó slack, esse
cálculo passa a ser possível, pois o valor da derivada do
módulo da tensão do nó slack, com relação ao módulo da
tensão de qualquer outro nó, é igual a zero.
(5)
Portanto, partindo do nó slack em direção aos nós terminais,
é possível o cálculo de todas as derivadas parciais.
III. DERIVADA DO MÓDULO DA TENSÃO EM UM NÓ
EM RELAÇÃO AO FATOR DE CARREGAMENTO DO
SISTEMA
O fator de carregamento multiplica todas as cargas por um
número, que reflete a carga do sistema para aquele momento
em função da carga nominal. Portanto, as potências-somas
nos nós serão dadas por:
Psk =
Qsk =
linhas
nos
i =1
linhas
i =1
nos
i =1
i =1
Peri + Fc ⋅
Qeri + Fc ⋅
Pi
(6)
Qi
(7)
Derivando (6) e (7) com relação a Fc, tem-se:
∂Psk linhas Peri nos
=
+ Pi
∂Fc
i =1 ∂Fc
i =1
∂Qs k linhas Qeri nos
=
+ Qi
∂Fc
i =1 ∂Fc
i =1
(
−
1
2
2⋅ A
)
1
−
1
∂B
∂C
⋅ B2 − 4 ⋅ A ⋅ C 2 ⋅ 2 ⋅ B ⋅
−4⋅
2
∂F
∂F
c
c
2⋅ A
2⋅ A
∂Vslack
=0
∂V j
+
B2 − 4 ⋅ A ⋅ C
(8)
(9)
Assim, a derivada parcial da tensão com relação ao fator de
carregamento é dada por:
(10)
IV. LINERIZAÇÃO
Através de simulações em sistemas radiais de distribuição de
energia elétrica, verificou-se que, variando a tensão na saída
de um regulador, as tensões dos nós localizados a jusante
deste experimentam variações bem semelhantes, como se
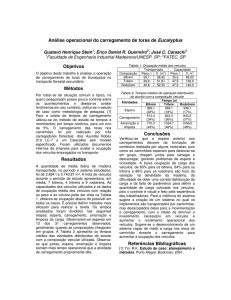
pode observar na figura 1. Além disso, um incremento de
tensão V na saída do regulador provoca incrementos de
tensão nos nós a jusante, aproximadamente proporcionais a
V. Levando em conta essa relação linear, pode-se estimar a
tensão de um nó [5] alimentado pelo regulador através da
equação:
∂V
Viestimado = Vicalculado + i ⋅ ∆V j
(11)
∂V j
No caso do fator de carregamento, acontece um fato
semelhante: quando se varia o fator de carregamento em um
sistema radial, o perfil de tensão varia de maneira
aproximadamente proporcional.
Assim como no caso anterior será utilizada uma aproximação
linear para poder calcular o valor do módulo da tensão para
qualquer carregamento, dentro da excursão usual da curva de
carga. Portanto, de posse do valor das derivadas parciais e
dos valores dos módulos das tensões para o caso base, temse:
∂V
Viestimado = Vicalculado + i ⋅ ∆Fc
(12)
∂Fc
No caso em que houver variações simultâneas de
carregamento no sistema e de tensão na saída do regulador, a
equação geral é dada por:
∂V
∂V
Viestimado = Vicalculado + i ⋅ ∆V j + i ⋅ ∆Fc (13)
∂V j
∂Fc
∂Vi
também deverá iniciar da SE, pelo mesmo
∂Fc
motivo alegado na seção anterior, ou seja:
∂Vslack
=0
(14)
∂Fc
O cálculo de
V. ALGORITMO
A determinação dos parâmetros de sensibilidade, tanto para a
derivada parcial com relação ao módulo da tensão como com
relação ao fator de carregamento deverão ser feitos, dentro de
um cálculo de fluxo de carga, de modo semelhante, seguindo
o procedimento:
1.
2.
3.
4.
5.
6.
Inicializar as variáveis de acordo com os dados de
entrada;
Executar uma iteração de fluxo de carga;
Partindo da subestação em direção aos nós
∂Vk
∂Vk
terminais, calcular
através de (4) e
∂Fc
∂V j
através de (10).
Testar convergência;
Voltar ao passo 2 até que o processo tenha
convergido;
Imprimir os resultados
VI. RESULTADOS
Para poder confirmar as hipóteses de linearidade entre as
variáveis apresentadas neste trabalho, realizaram-se
simulações com redes reais.
Inicialmente, escolheram-se sistemas de distribuição com
reguladores de tensão instalados. Posteriormente, foram
executados cálculos de fluxo de carga, nos quais se variou a
tensão na saída dos reguladores. Em seguida, verificou-se o
comportamento do módulo da tensão em alguns nós. O
gráfico 01 mostra o comportamento dessas tensões como
conseqüência de uma variação da tensão na saída do
regulador.
1
1,1
0,95
1,05
1
N4
N8
N14
N18
N21
0,95
Tensao (pu)
Tensão no nó (p.u.)
0,9
21.0
11.0
7.0
34.0
0,85
0,8
0,75
0,9
0,7
0.5
0.75
1.0
1.25
1.5
Carregamento
0,85
1,01 p.u.
1,03 p.u.
1,05 p.u.
1,07 p.u.
Tensão na saída do regulador (p.u.)
Fig. 1. Variação do módulo da tensão em nós remotos ao regulador
em função do módulo da sua tensão de saída.
Pode-se observar na figura 01 que as tensões apresentam um
comportamento linear com a variação da tensão de saída do
regulador. No caso dos nós N8, N14, N18 e N21 as tensões
cresceram proporcionalmente com a tensão de regulação. Já
o nó N4, sua tensão se manteve constante. Isso ocorre pelo
fato de que o nó N4 está a montante do nó de saída do
regulador, não sofrendo o efeito da variação da tensão na sua
saída. Portanto, para nós i como o nó N4, pode-se adotar a
aproximação:
∂Vi
=0
(15)
∂V j
Para verificar a validade da relação de linearidade entre o
módulo da tensão em função do fator de carregamento, foram
realizados outros cálculos de fluxo de carga, só que desta
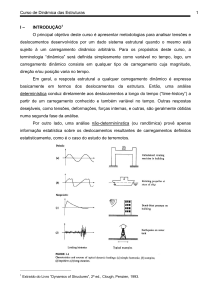
vez, variou-se o fator de carregamento do sistema. A figura
02 mostra o efeito desta variação nas tensões de alguns nós
localizados ao longo do alimentador.
Fig. 2. Variação do módulo da tensão nos nós de um alimentador
em função do fator de carregamento.
Observando a figura 02, pode-se notar que o efeito da
variação do módulo da tensão nos nós do sistema em função
da variação do carregamento também ocorre de forma
aproximadamente linear.
Posteriormente, utilizando o algoritmo descrito, foram
calculadas as derivadas do módulo das tensões de um
alimentador com relação ao módulo de uma tensão
específica. Para isto foi escolhido um sistema de 53 nós e
uma potência instalada de 2,5 MVA. A figura 03 mostra a
comparação da tensão calculada por um fluxo de carga real
(linha azul) e pelo processo de linearização (linha vermelha).
1,01
0,99
0,97
Tensão (pu)
0,95
calc
est
0,93
0,91
0,89
0,87
0,85
1
3
5
7
9
11
13
15
17
19
21
23
25
27
29
31
33
35
37
39
41
43
45
47
49
51
Nó
Fig. 3. Comparação entre o valor do módulo da tensão calculado
por um fluxo de carga (linha azul) e pelo processo baseado em
linearização (linha vermelha), calculado pela equação 11.
A fim de verificar a validade da linearização, no caso em que
se deseja estimar o valor do módulo da tensão após um
aumento do carregamento do sistema, realizou-se uma
simulação utilizando um sistema de 23 nós e um
carregamento de 2,3 MVA. Após a execução do caso base e
do cálculo dos parâmetros de sensibilidade, as cargas do
alimentador foram aumentadas em 50%. Para essa nova
configuração, executou-se um novo cálculo de fluxo de carga
e compararam-se as tensões obtidas com as encontradas
através do processo de linearização. A figura 04 mostra essa
comparação, onde a linha azul representa as tensões obtidas
pelo cálculo de fluxo de carga e a linha vermelha, pelo
processo linearizado.
1,05
1
0,95
0,9
0,85
Real 1,5
Est 1,5
0,8
alimentadores de distribuição, para fins de análise de
regulação, haja vista que o maior incremento conseguido
com reguladores de tensão é de 15%, quando se utiliza
conexões em delta fechado.
Na segunda comparação, o erro máximo encontrado foi de
3,0% para um aumento do carregamento de 50,0%. Pode-se
notar que, para esse incremento, o sistema não se encontra
mais na região de funcionamento de interesse, para os
objetivos de regulação de tensão, pois uma variação tão
elevada, em torno do ponto de operação, pode ser
considerada excessiva. Contudo, aumentos muito maiores
que 50,0% para carregamento com relação ao caso base,
podem ser considerados em simulações de planejamento.
Nesses casos, recomenda-se executar um novo cálculo de
fluxo de carga.
VII. CONCLUSÃO
O cálculo do valor dos módulos das tensões nos nós de um
alimentador através de um modelo linearizado, tomando
como base um único cálculo de fluxo de carga e os
parâmetros de sensibilidade é algo pouco utilizado. Isso se
deve ao fato de que os computadores modernos têm alta
velocidade de processamento e memória em abundância.
Além disso, esse tipo de cálculo é realizado, geralmente, na
fase de planejamento da operação de sistemas, situação em
que o tempo de processamento não se impõe como uma
limitação de todo o processo. Sendo muito mais eficiente a
execução de um novo cálculo de fluxo de carga.
Entretanto, em algumas aplicações, onde variáveis como
tempo e capacidade de processamento são limitadas,
aproximações podem ser justificadas. No caso em que as
simulações precisam ser realizadas em tempo real, com
limitações de memória e capacidade de processamento, o
algoritmo aqui apresentado pode ter uma aplicação bastante
útil, tendo em vista que os erros envolvidos são
insignificantes, dentro da faixa em que as tensões precisam
ser estimadas.
0,75
AGRADECIMENTOS
0,7
0,65
0,6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Fig. 4. Comparação entre o valor do módulo da tensão calculado
por um fluxo de carga (linha azul) e pelo processo de linearização
(linha vermelha) definido pela equação 12.
Comparando os resultados apresentados na figura 03,
observa-se que o erro máximo encontrado foi de 0,7%, para
um incremento de tensão de aproximadamente 15%. Nos
testes realizados em outros sistemas o resultado foi
semelhante. Um fato importante que se deve salientar é que
quanto maior for o incremento de tensão no nó regulado,
maiores serão os erros encontrados no processo, devido à
região de validade da linearização. Entretanto, esse fato não
causa problema para o caso de estimativas de tensões de
Os autores agradecem à CAPES pelo suporte financeiro,
correspondente à concessão de uma quota de bolsa de
doutorado.
REFERÊNCIAS
[1] M. F. Medeiros Jr., M. C. Pimentel Filho, “Optimal
Power Flow in Distribution Networks by Newton’s
Optimization Methods”, Proceedings of the 1998
IEEE International Symposium on Circuits and
Systems, Montrey, CA 1998.
[2] M. F. Medeiros Jr., M. C. Pimentel Filho, J. A. Nicolau
de Oliveira, “Three-phase models of Voltage
Regulators for the Power Summation Load Flow”. VI
INDUSCON, Joinville – SC, 2004.
[3] R. Cespedes. "New Method for the Analysis of
Distribution Networks". IEEE Transactions on Power
Delivery, Vol. 5, Jan 1990.
[4] M. F. Medeiros Jr., M. C. Pimentel Filho, "Fluxo de
Potência Trifásico pelo Método Soma de Potências:
Modelagem de Ajustes e Controles". V INDUSCON,
Salvador – BA, 03 a 05 de julho de 2002.
[5] M. F. Medeiros Jr., M. C. Pimentel Filho, “Localização
ótima de bancos trifásicos de reguladores de tensão
em alimentadores radiais de distribuição”. CBA 2002,
Natal – RN, 02 a 05 de setembro de 2002.