Manual do usuário – Heráclito Versão 1.0 – 2013 Bem

Manual do usuário – Heráclito Versão 1.0 – 2013
Bem-vindo ao tutorial do Heráclito
Este tutorial foi concebido para ajudar você a começar a usar o Heráclito para fazer
provas de lógica.
O Heráclito se apresenta aos seus usuários como um objeto de aprendizagem que têm
por objetivo auxiliar os alunos em como elaborar provas de argumentos formais por
meio das regras da Dedução Natural.
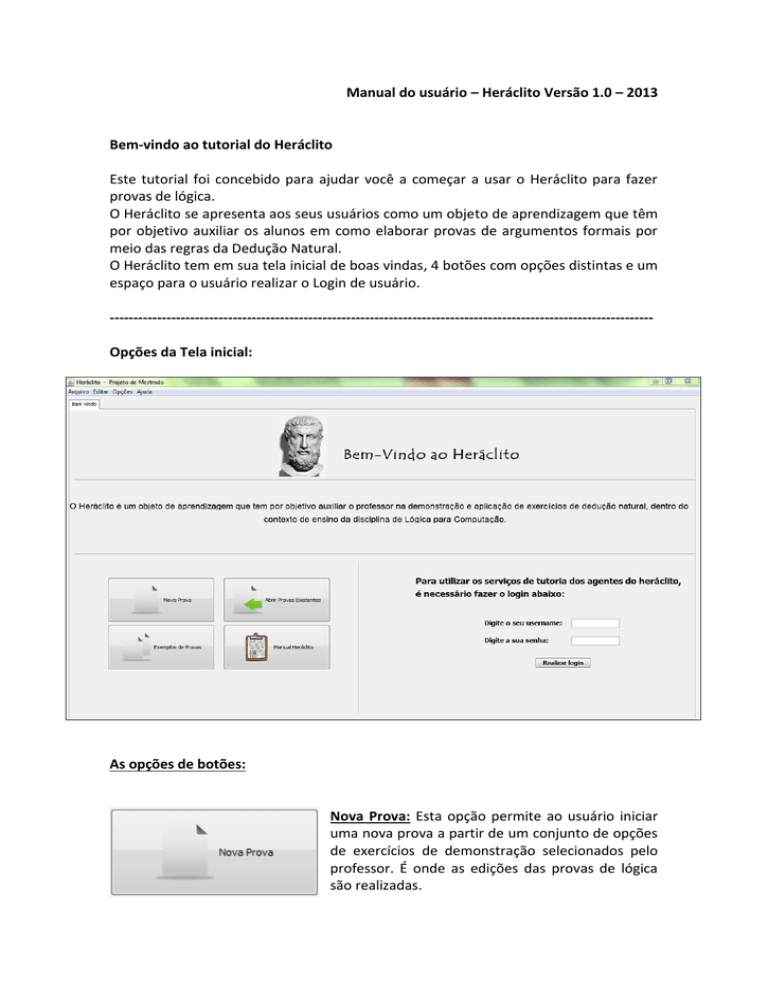
O Heráclito tem em sua tela inicial de boas vindas, 4 botões com opções distintas e um
espaço para o usuário realizar o Login de usuário.
------------------------------------------------------------------------------------------------------------------Opções da Tela inicial:
As opções de botões:
Nova Prova: Esta opção permite ao usuário iniciar
uma nova prova a partir de um conjunto de opções
de exercícios de demonstração selecionados pelo
professor. É onde as edições das provas de lógica
são realizadas.
Uma vez selecionado o botão Nova Prova, uma segunda tela com edição de provas
será aberta (em guias). Esta tela é a principal interface do Heráclito com o usuário. E
pode ser visualizada na figura abaixo:
É nesta tela que os argumentos formais são provados.
Esta tela é composta por botões laterais os quais representam as regras de inferências
básicas e derivadas.
Para dar inicio a provação do argumento é necessário primeiramente escolher o nível
do argumento (Básico, Intermediário ou Avançado). Após escolher o nível uma lista
com exercícios é mostrada. Escolhe-se o exercício e o processo de edição é iniciado
(com ajuda dos botões laterais).
A demonstração é elaborada passo-a-passo com base na aplicação das regras de
inferência (básica e derivada).
Exemplos de Provas: Esta opção dá acesso a
argumentos já provados, elaborados pelo professor
e é composta por uma série de exercícios que
foram divididos em 3 níveis de complexidade:
inicial, intermediaria e avançada.
Nível 1 (básico) Exercícios:
Este conjunto de exercícios é projetado para que você possa experimentar as regras
básicas.
Nível 2 (Intermediário) Exercícios:
Este conjunto de exercícios é projetado para você experimentar uma combinação de
regras.
Nível 3 (Avançado) Exercícios:
Este conjunto de exercícios consiste em alguns argumentos interessantes e mais
difíceis (de maior complexidade).
Abrir Provas Existentes: Esta opção dá acesso às
provas feitas pelo aluno que foram testadas e
salvas no computador (podendo ser abertas ou
retomadas a qualquer momento);
Manual do Heráclito: manual de instruções e de
funcionamento da ferramenta.
Uma vez instalado no computador do aluno, o Heráclito poderá se comportar como
um editor de provas que permite ao aluno resolver os problema de demonstração,
mas não oferece nenhum suporte pedagógico. Este tipo de funcionalidade estará
disponível a partir do login do usuário, que depois de realizado com sucesso, terá o
suporte pedagógico habilitado, tendo acesso aos agentes de apoio pedagógico para o
ensino de Lógica, disponibilizados pelo servidor MILOS.
------------------------------------------------------------------------------------------------------------------O Login do usuário:
Para usar os serviços de tutoria do Heráclito é necessário realizar Login. O usuário é
cadastrado previamente e recebe um usuário e uma senha do sistema.
Ao realizar o login com este usuário e senha, você estará logado com o servidor,
podendo usufruir dos serviços oferecidos pela ferramenta.
Nesse processo, é possível contar com agentes de software, em especial com o agente
mediador, que tem um papel estratégico (no desenvolvimento pedagógico), mediando
e participando ativamente no desenvolvimento do exercício.
Esta opção não é obrigatória, podendo usar o Heráclito como editor de provas. Porém,
a não realização do login, implica na não habilitação dos agentes (sem suporte).
Enquanto você estiver utilizando o Heráclito na resolução dos exercícios, Agentes de
Software estarão monitorando suas ações e um Tutor estará pronto para ajudar você.
Se você estiver preso em fazer uma prova, você poderá pedir dicas ou sugestões a este
tutor por meio do botão Ajuda.
Alternativamente, você poderá usar este botão Ajuda do Heráclito, a qualquer
momento da prova.
------------------------------------------------------------------------------------------------------------------O tutor Mediador
O tutor Mediador do Heráclito é um agente de software que visa ajuda-lo na resolução
dos exercícios, fazendo o papel do professor.
Ao utilizar o Heráclito, é possível obter “ajuda” do "Tutor", através do diálogo, por
meio do botão ajuda. O Tutor Mediador usa um conjunto de estratégias de
aprendizagem, especificas para Lógica, ao ajudar você a fazer uma prova de Dedução
Natural.
------------------------------------------------------------------------------------------------------------------O botão Ajuda do Heráclito
Este arquivo de ajuda foi projetado para ajudar você a usar o Heráclito e não para
ensinar Lógica ou ensinar conceitos de regras de aplicação de Lógica.
Na opção de ajuda é possível encontrar suporte:
- Quando logado no sistema Heráclito: É possível ter suporte ao manual do Heráclito,
uso das regras, exemplos de resolução de exercícios, auxílio dos agentes com dicas
para o próximo passo (regras).
- Quando não logado no sistema Heráclito: É possível ter suporte ao manual do
Heráclito e uso de regras e exemplo de resolução de exercícios.
Como resultado, um conhecimento básico de lógica e dedução natural é assumido por
toda esta ajuda.
Para navegar neste documento é possível usar a exibição de árvore à esquerda da
janela, clicando nos ícones para exibir seu conteúdo.
------------------------------------------------------------------------------------------------------------------Como usar as regras de Dedução na Lógica Proposicional?
Regras aplicáveis:
Redução ao Absurdo (raa):
Para provar a redução ao absurdo devemos criar uma nova hipótese que nos seja útil
ao final do raa, nesse caso criamos a hipótese P (hip-raa) uma das condições para se
utilizar a redução ao absurdo, e para utilizar o modus ponens e obter o Q para que
com a adição se consiga a outra condição para se usar o raa, o QQ.
PQ, Q ├─ P
1
2
3
4
5
6
PQ
Q
│P
│Q
│ QQ
P
hip
hip
hip-raa
1,3 mp
2,4 cj
3-5 raa
Prova Condicional (pc):
Para provar PR a partir de PQ e QR criamos uma hipótese (como na redução ao
absurdo), criamos P para deduzir o modus ponens de PQ para obtermos Q e assim
conseguir deduzir outro modus ponens e obter R, com o P no inicio da demonstração
da prova condicional e R no final, de acordo com a regra da prova condicional,
podemos obter PR.
PQ, QR ├─ PR
1
2
3
4
5
6
PQue
QR
│P
│Q
│R
PR
hip
hip
hip-pc
1,3 mp
2,4 mp
3-5 pc
Conjunção (cj):
O “e” lógico exige que as duas fórmulas sejam verdadeiras para se obter o resultado
verdadeiro, então para se usar a regra da conjunção deve-se ter P e Q provados.
P, Q ├─ PQ
1
2
3
P
Q
PQ
hip
hip
cj 1,2
Adição (ad):
Sabemos que se uma fórmula P é verdadeira, então entre P e uma fórmula arbitrária
Q, ao menos uma é verdadeira. Uma delas sendo verdadeira, pela regra do “ou” lógico,
a outra tanto faz se é falsa ou verdadeira, sempre será verdadeiro, podendo assim
adicionar qualquer fórmula.
P ├─ PQ
1
2
P
P Q
hip
ad 1,2
Introdução da Equivalência (+eq):
Para termos uma bi implicação é necessário que a implicação de P para Q seja
verdadeira, assim como de Q para P também.
PQ, QP ├─ PQ
1
2
3
PQ
QP
PQ
hip
hip
+eq 1,2
Dupla Negação (dn):
Negar a negação de P é tornar P verdadeiro.
¬¬P├─ P
1
2
¬¬P
P
hip
dn 1
Modus Ponens (mp):
O argumento tem duas premissas. A primeira premissa é a condição "se - então",
nomeadamente que P implica Q. A segunda premissa é que P é verdadeiro. Destas
duas premissas pode ser logicamente concluído que Q tem de ser também verdadeiro.
PQ, P ├─ Q
1
PQ
hip
2
3
P
Q
hip
mp 1, 2
Simplificação (sp):
Sabemos que para que PQ seja verdadeiro, P e Q tem que ser verdadeiros, então é
possível simplificar essa fórmula deduzindo qualquer uma das premissas, pois as duas
são verdadeiras.
PQ ├─ Q
1
2
PQ
Q
hip
sp 1
Eliminação da Disjunção (-dj):
PQ, PR, QR├─ R
1
2
3
4
PQ
PR
QR
R
hip
hip
hip
-dj 1, 2, 3
Eliminação da Equivalência (-eq):
Se a bi implicação for verdadeira significa que a implicação de P para Q e de Q para P
são verdadeiras, então pode-se deduzir tanto uma quanto a outra a partir dessa bi
implicação.
PQ ├─ PQ
1
2
PQ
PQ
hip
-eq 1
Modus Tollens (mt):
A primeira premissa é a P implica Q. A segunda premissa é que Q é falso. Destas duas
premissas pode ser logicamente concluído que P tem de ser falso. (Por quê? Porque se
P fosse verdadeiro, então Q seria verdadeiro, pela premissa 1, mas não é pela premissa
2).
PQ, Q ├─ P
1
2
3
PQ
Q
P
hip
hip
mt 1, 2
Silogismo Disjuntivo (sd):
Se ¬P é verdadeiro, logo P é falso, então Q obrigatoriamente tem que ser verdadeiro
para a premissa PQ ser verdadeira.
PQ, ¬P ├─ Q
1
2
3
PQ
¬P
Q
hip
hip
sd 1
Exportação (exp):
De se P e Q são verdadeiros então R é verdadeiro, podemos demonstrar se Q é
verdadeiro então R é verdadeiro, se P é verdadeiro.
(PQ)R ├─ P(QR)
1
2
(PQ)R
P(QR)
hip
exp 1
Silogsimo Hipotético (sh):
Se o primeiro implica o outro e o outro implica o terceiro, então o primeiro implica o
terceiro, de acordo com a propriedade da transitividade da implicação.
P  Q, Q  R├─ P  R
1
2
3
PQ
QR
PR
hip
hip
sh 1, 2
DC:
PQ, PR, QS ├─ RS
1
2
3
4
PQ
PR
QS
RS
hip
hip
hip
dc 1, 2, 3
Inconsistência (inc):
Se as premissa P é verdadeira e a ¬P também é verdadeira, só se pode deduzir um
argumento diferente de P, nesse caso, Q.
P, P ├─ Q
1
2
3
P
¬P
Q
hip
hip
inc 1, 2
Agora vejamos como construir uma dedução usando as regras de inferência diretas.
Vamos provar o seguinte argumento:
A  B, A ├─ B  C
O primeiro passo é colocar cada premissa (hipótese) em uma linha enumerada:
1
2
AB
A
hip
hip
Agora, aplicamos as regras de inferência que julgarmos úteis para chegar ao resultado
esperado. Para cada nova fórmula inferida, inserimos uma linha enumerada, indicando
à direita as linhas que contém as fórmulas a partir das quais foi efetuada a inferência,
assim como a regra aplicada.
1
2
3
4
AB
A
B
BC
hip
hip
mp 1, 2
ad 3
Aplicamos nas linhas 1 e 2 o Modus Ponens (mp) e logo depois adicionamos o C ao B
para chegarmos na resposta que o argumento exigia.