Lista 1 - Conceitos de Tensao e deformacao

EXERCÍCIOS DE RESISTÊNCIA DOS MATERIAIS 1
AULA 1 – CONCEITOS DE TENSÃO E DEFORMAÇÃO
1. Uma placa é fixada a uma base de madeira por meio de três parafusos de
diâmetro 22mm. Calcular a tensão média de cisalhamento nos parafusos para
uma carga P=120 kN, conforme mostra a figura abaixo.
R – τ = 105,2 MPa
2. Determinar a tensão normal de compressão mútua (ou tensões de
“contato"ou tensão de “esmagamento") da figura abaixo entre:
a) o bloco de madeira de seção 100mm x 120mm e a base de concreto 500mm
x500mm x 60mm.
b) a base de concreto e o solo.
R- a) ζ = 3,33 MPa b) ζ=0,16 MPa
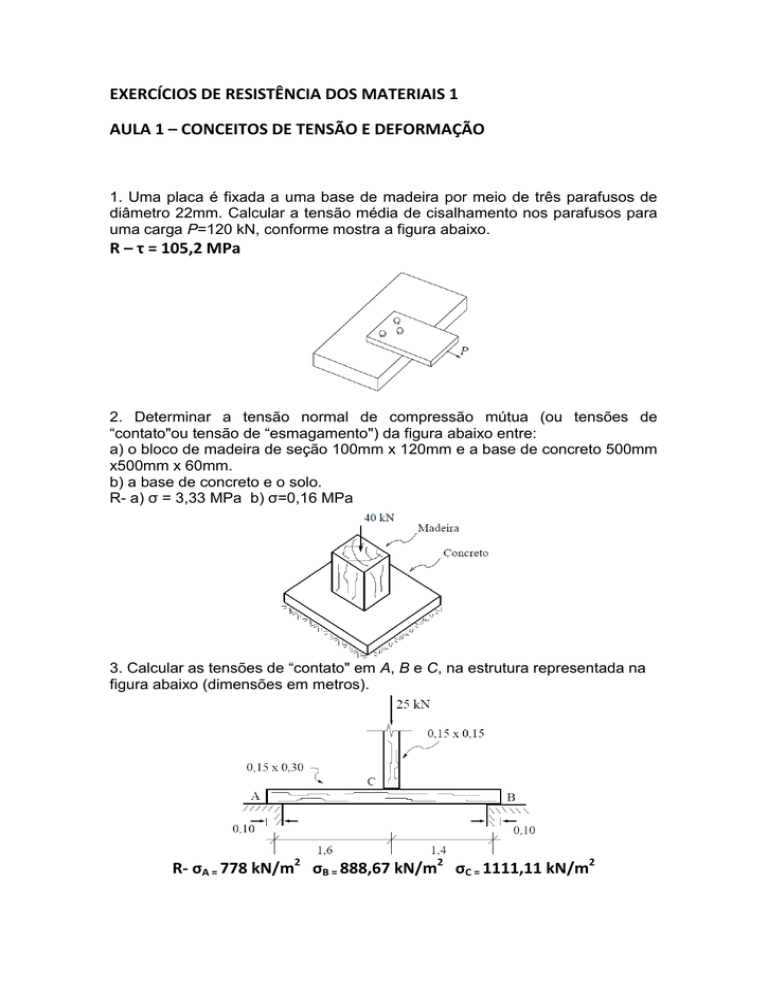
3. Calcular as tensões de “contato" em A, B e C, na estrutura representada na
figura abaixo (dimensões em metros).
R- σA = 778 kN/m2 σB = 888,67 kN/m2 σC = 1111,11 kN/m2
4. Uma chapa deve ser furada por punção, exercendo-se no perfurador uma
tensão de compressão de 420 MPa. Na chapa, a tensão de ruptura ao corte é
de 315 MPa;
a) Calcular a espessura máxima da chapa para fazer um furo de 75 mm de
diâmetro;
b) Calcular o menor diâmetro que pode ter o furo, se a espessura da chapa é
de 6mm.
R – e ≥ 25 mm
d ≤ 18 mm
5: A barra abaixo tem largura de 35 mm e espessura de 10 mm, constantes ao
longo de seu comprimento. Determine as tensões normais nos diferentes
trechos da barra para o carregamento abaixo.
R- σAB = 34,3 MPa σBC = 85,7 MPa σCD = 62,4 MPa
6: Determine as tensões nos pinos localizados em A e B com diâmetros d= 8
mm e a tensão na barra BC para o conjunto abaixo:
R – τA = 142,2 MPa
τB = 332,2 MPa
σBC = 334 MPa
7: Determine o diâmetro da barra BC, se a tensão admissível é σadm =155
MPa. A viga é assumida ser parafusada em A.
R – dBC = 11,1 mm
8: Duas vigas de madeira são conectadas por um parafuso em B. Assumindo
que as conexões em A, B, C, e D exercem somente forças verticais nas vigas.
Determine o diâmetro do parafuso em B e o diâmetro externo de sua arruela se
a tensão admissível do parafuso é σadm p. = 150 MPa e a tensão admissível da
madeira é σadm m. = 28 MPa.
R- dparafuso = 6,1 mm
darruela = 15,4 mm
9. Determine a máxima força F que pode ser aplicada na estrutura se as áreas
das seções transversais das barras são A = 5000 mm 2 e a tensão admissível
de tração é σadm t = 14 kgf/mm2 e a tensão admissível de compressão é σadm c
= 10,5 kgf/mm2 .
R - F = 9276 kgf
10: A estrutura treliçada abaixo suporta duas forças de 12 t. Se as tensões
admissíveis são σadm t = 14 kgf/mm2 em tração e σadm c = 10,5 kgf/mm2 em
compressão, determine a menor seção transversal possível para as barras.
11-Um tubo circular de alumínio de comprimento L=500 mm é carregado em
compressão por forças P. Os diâmetros externo e interno têm 60 mm e 50 mm,
respectivamente. Um medidor de deformação é colocado na superfície externa
da barra para medir deformações normais na direção longitudinal.
a) Se a deformação medida é ε = 540x10 -6, qual é o encurtamento δ da
barra?
b) Se a tensão de compressão na barra deve ser de 40 MPa, qual deveria
ser a carga P?
R- a) δ = 0,270 mm
b) P = 34,6 kN
12- Um guindaste de carregamento formado por uma viga ABC sustentada por
um cabo BD é submetido à carga P. O cabo tem uma área de seção
transversal efetiva A=481 mm2. As dimensões do guindaste são H=1,6 m, L 1 =
3,0 m e L2 = 1,5 m.
a) Se a carga P = 32 kN, qual é a força de tração média no cabo?
b) Se o cabo sofrer um estiramento de 5,1 mm, qual é a deformação
média?
R- a) ζ = 212 MPa
b) ε = 1500 x 10-6
13- Uma placa quadrada de concreto armado cujo peso específico é de 2,4
kN/m3, de 2,5 m de lado e 225mm de espessura é levantada por quatro cabos
conectados em seus vértices. Os cabos são conectados em um gancho em um
ponto 1,6 m acima da placa. Cada cabo tem uma área de seção transversal
efetiva de A=190 mm2. Determine a s tensões de tração nos cabos devido ao
peso da placa.
R – ζ = 66,2 MPa
14- Um membro tubular em suporte deve transmitir uma força axial de
compressão P=49k. A espessura da parede do tubo deve ser de 0,4 in. Qual é
o diâmetro externo mínimo necessário dmín se a tensão de compressão
admissível é de 9500psi?
R- d = 4,5 in