2ª Aulado cap. 06 Força de Arrasto

2ª Aula do cap 06
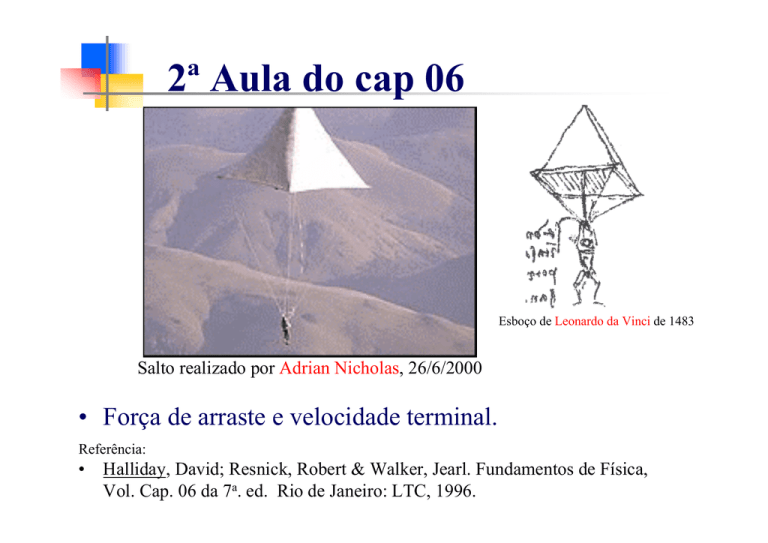
Esboço de Leonardo da Vinci de 1483
Salto realizado por Adrian Nicholas, 26/6/2000
• Força de arraste e velocidade terminal.
Referência:
•
Halliday, David; Resnick, Robert & Walker, Jearl. Fundamentos de Física,
Vol. Cap. 06 da 7a. ed. Rio de Janeiro: LTC, 1996.
Força de arraste e velocidade terminal
A força de arraste em um fluido é uma força dependente da
velocidade (ao contrário da força de atrito vista até agora) e
apresenta dois regimes:
a) Fluxo turbulento: velocidades altas
b) Fluxo viscoso: velocidades baixas
Fluxo turbulento
Força de arraste:
1
2
2
FD = ρAC D v = dv
2
Coeficiente de arraste
Área da seção transversal do corpo
Densidade do meio
Velocidade terminal e queda de corpos.
1
2
FD = ρAC D v
2
∑F = 0→ F
D
FD
= mg
mg
Exemplo da gota de chuva
(Halliday, Resnick)
vT =
2mg
ρAC D
vT ≈ 27 km / h
Sem a resistência do ar:
vT ≈ 550km / h
Velocidade terminal e queda de corpos
1
2
FD = ρAC D v
2
Velocidade terminal de uma gota de chuva
Ex.: 1) Uma gota de chuva com raio r = 1,5 mm cai de
uma nuvem que está a uma altura de h = 1200 m. O
coeficiente de viscosidade para a gota é 0,6. Suponha
que a gota seja esférica durante a queda. Determine a
velocidade terminal desta gota? (velocidade limite).
ρ água = 1000 kg/m3 e ρ ar = 1,2 kg/m3 . Qual seria a
velocidade da gota ao chegar ao solo se não houvesse a
força de arrasto.
R = 1,5 mm
Velocidade terminal de uma gota de chuva
vT =
2mg
ρAC D
R = 1,5 mm
H = 1200 m
vT ≈ 27 km / h
Velocidade terminal de uma gota de chuva
sem força de arraste…
vT ≈ 550km / h
Fluxo viscoso: exemplo simples de
aplicação de equações diferenciais
Força de arraste nesse caso:
FD = 6πηrv = bv
Raio do objeto
Coeficiente de viscosidade
Velocidade terminal:
mg
v=
6πη r
Questão: como a velocidade aumenta
até alcançar a velocidade terminal?
Variação da velocidade em fluxo viscoso
∑ F = mg − bv = ma
b = 6πη r
b
dv
'
ma = m
= m( g − v ) = m( g − b v )
dt
m
Solução:
dv
'
= g−bv
dt
b
−
t
g
v = ' (1 − e m )
b
Velocidade terminal
b
b =
m
'
Solução…
dv
'
= g−bv
dt
g
v = ' (1 − e
b
Que é igual a
b
− t
m
)
dv
gb
=
e
dt b' m
g − b' v !!!
−
b
t
m
= ge
−
b
t
m
Exemplo:
Os blocos estão em movimento com velocidade
constante. m1=m2=14 Kg; θ = 300 - Calcule: fk e μk
v
V const.
Exemplo: Diagrama de corpo livre
m1=m2=14 Kg; θ = 300 - Calcule: fk e μk
m1=m2=14 Kg; θ = 300 - Calcule: fk e μk
V const.
m1=m2=14 Kg; θ = 300 - Calcule: fk e μk
V const.