Máquinas Eléctricas
Motores assíncronos
Métodos de arranque
Modos de arranque, de forma a que os accionamentos, com motor de corrente alternada
assíncrono, satisfaçam os seguintes requisitos:
ž
ž
ž
ž
Aceleração controlada
Tempo de arranque controlado
Limitação do aquecimento dos enrolamentos
Intensidade de corrente absorvida e queda de tensão admissíveis
Métodos para controle do arranque:
Æ
Æ
Æ
Electromagnético
Electromecânico
Por semicondutores
Gaiola de esquilo
Electromagnéticos
Neste tipo de motor, não existe a possibilidade de intervir sobre o circuito eléctrico do rotor.
Assim, o comportamento do motor é um compromisso entre o binário e a corrente.
Arranque directo
Forma mais simples, segura e mais utilizada. O motor é ligado directamente à rede de
alimentação sem qualquer dispositivo. A corrente de arranque sobe a valores que variam de 4 a 8
vezes a corrente nominal. Em Portugal este tipo de arranque está
condicionado pela legislação existente1 . Na figura 1 pode ver-se um
circuito de potência para arranque directo, através de contactores2 .
As situações em que não se deve utilizar arranque directo,
referem-se aos casos em que o binário motor excede de tal forma o
binário resistente que o binário acelerador se torna demasiado elevado,
o que coincidirá com uma inércia total de accionamento baixa. Como
consequência, a aceleração pode ser excessiva e levantar problemas,
tais como:
ž Roturas nos elementos mecânicos da máquina e da
transmissão
ž Falta de conforto, no caso de veículos
ž Reduzida exactidão, se tiver que se parar a máquina
numa posição determinada
Figura 3.1
Arranque por resistências em série com enrolamentos estatóricos
1
2
RSIUEE – § ...
Interruptores de potência elevada, comandados por bobines electromagnéticas
1/17
Máquinas Eléctricas
Motores assíncronos
Método de arranque por redução da tensão de alimentação. A tensão de alimentação
condiciona directamente o fluxo, reduzindo, consequentemente, a corrente absorvida e o binário
motor em cada momento. Esta dependência expressa-se por:
TM 1 V1
=
TM 2 V2
2
e
I1 V1
=
I 2 V2
Dispondo de 3 resistências (Rad), em série com as fases de alimentação (figura 3.2 ) verificarse-á uma queda de tensão óhmica (∆V), o que diminuirá o valor da
V1
tensão aos terminais do motor (V2 ) bem como a corrente absorvida
por este. Embora este método seja adequado do ponto de vista da
∆V
instalação eléctrica, tem o inconveniente das perdas de Joule –
3x RadI2 x t – que se verificam nas resistências adicionais, energia que
V2 = V1 - ∆V
não é aproveitada para realizar qualquer trabalho útil. É empregue
M
2
em motores pequenos (I ( logo RI () ou em motores com frequências
3
de arranque reduzidas (t ()
À medida que o motor se vai aproximando da velocidade de Figura 3.2
trabalho nominal, a corrente reduziu-se bastante (para In ) e, portanto,
a queda de tensão é pequena, não havendo uma variação brusca
I
de binário e de corrente ao retirar as resistências de serviço. A
tensão varia, assim, continuamente aproximando-se do valor
nominal quando se aproxima da velocidade final, dando,
portanto, uma forma de arranque bastante suave. Nalguns casos
n
particulares empregam-se resistências líquidas, que têm a
Figura 3.3
característica de, ao aquecerem, diminuírem a sua resistência,
proporcionando um arranque ainda mais suave.
Como a intensidade é máxima no momento do arranque
(motor parado, g = 1), dimensionam-se as resistências para este
ponto de funcionamento. O método de dimensionamento
simplifica-se, ao verificar-se que com g = 1 as correntes são tão
elevadas, que a corrente de vazio Im é relativamente reduzida,
fazendo com que o circuito equivalente seja uma associação, em
série, das impedâncias do rotor e do estator. Considerando que os
motores com gaiola de esquilo se caracterizam pela proporção
entre as suas resistências e as suas impedâncias:
k=
R1 + R2'
X 1 + X 2'
e que, em função das resistências adicionais, podemos
expressá-las pela relação:
F=
Rad
X1 + X 2'
Figura 3.4
poderemos calcular a redução de corrente obtida e, posteriormente, elevá-la ao quadrado
para obter a redução de binário, no momento do arranque:
2/17
Máquinas Eléctricas
I a'
=
Ia
1 + (1 k )
Motores assíncronos
2
(1 + F )2 + (1 k )2
Na generalidade dos casos, bastará utilizar os gráficos do anexo A. Para uma determinação
mais apurada teria que empregar-se o circuito equivalente do motor.
Quando se pretende apenas a redução do binário de arranque, de forma a obter acelerações
mais suaves e não havendo problemas na criação de assimetrias na rede de
V1
alimentação, pode utilizar-se uma única resistência, em série com qualquer uma
das fases. Neste caso, a redução da corrente é pequena nessa fase, havendo,
inclusive, um aumento da corrente nas restantes duas fases. A redução
importante de binário que se atinge, advém do desequilíbrio da alimentação, que
V2
V1 V1
provoca o surgimento de um campo magnético inverso.
M
3
Esta forma de arranque aplica-se em motores pequenos, que arrancam com
cargas suaves ou quase em vazio, e é económico em termos de equipamento.
Figura 3.5
Arranque por reactâncias em série com enrolamentos estatóricos
Método de arranque muito semelhante ao anterior, mas com a particularidade de se
substituírem as resistências por reactâncias muito indutivas. Aplicam-se em motores de maior
potência, já que nestes casos as correntes são bastante mais elevadas e, por consequência, as
perdas também. Para além do mais, resolve-se o problema da dissipação do calor nas
resistências. A sua aplicação em motores de média tensão, com os terminais de cada fase
acessíveis, e nos que fazem o neutro no exterior do motor, é usual instalar as reactâncias do lado
do neutro, dado que:
- teremos um menor isolamento para a reactância, já que esta se encontra perto do
neutro (válido para casos de neutro à terra)
- teremos um menor valor de correntes de curto circuito, causadas por avarias, já
que as impedâncias do motor limitam o seu valor
Empregam-se reactâncias de núcleo de ar, que, dada a sua linearidade, evitam que se entre
na zona de saturação, pelas elevadas correntes que se verificam no arranque.
Tal como no caso anterior, teremos:
R + R2'
k= 1
X 1 + X 2'
G=
X ad
X 1 + X 2'
I a'
1 + (1 k )2
=
Ia
1 + (G + 1 k )2
Arranque com transformador ou autotransformador
Em geral, quando se deseja modificar a tensão, socorremo-nos de
um transformador. Quando a relação de transformação não é muito
afastada ? da unidade e sempre que se deseja reduzir a tensão disponível, a
opção mais vantajosa, técnica e economicamente, é o auto-transformador.
Neste tipo de arranque, o auto-transformador possui uma ou várias
relações de tensão – ver figura 3.6 – mas a sua construção é mais
complicada e o seu custo é maior, embora tenha melhores características e
V3
V2
V1
Figura 3.6
3/17
Máquinas Eléctricas
Motores assíncronos
maior capacidade de adaptação aos requisitos. È dimensionado para
regimes intermitentes, e, por conseguinte, o seu volume e peso, por kVA,
são menores que no caso de um transformador para serviço contínuo.
Na figura 3.7 apresenta-se o circuito de potência para arranque com
auto-transformador de um só escalão. Consegue-se uma transição suave,
desde a 1ª fase do arranque – Q1, KM2 e KM1 fechados e KM3 aberto –
passando por uma fase intermédia – KM1 aberto – e terminando na fase
final – KM3 fechado e KM2 aberto.
Supondo que as tensões do primário e secundário do autotransformador são respectivamente V1 e V2 , a relação de transformação é:
rt =
V1
V2
Figura 3.7
quando se liga o motor à tensão V2 , resulta que:
- as correntes absorvidas do secundário, pelo motor, multiplicam-se por rt
- o binário motor multiplica-se por rt 2
O importante, aqui, é a corrente que o motor absorve da rede, que é, como em todos os
transformadores, rt vezes o valor absorvido do lado do secundário, pelo que, as correntes de linha
se multiplicam por rt 2 . Se se especificar um arranque no qual as correntes se multiplicam por um
coeficiente k < 1, a relação de transformação calcular-se-á por
rt = k
e os binários reduzem-se na relação de:
rt = k < 1
Esta forma de arranque, reduz, na mesma proporção, os binários e as correntes de linha,
pelo que, o índice de arranque – Nm/kVA – se mantém. Refira-se que, nos arranques já vistos
este índice piora, pelo que, este método tem as suas vantagens.
2
6
1,5
4,5
T1
I
3
0,5
1,5
0
0
1
0,8
0,6
0,4
0,2
0
1
0,8
0,6
0,4
0,2
0
Figura 3.8
O resultado deste tipo de arranque está evidenciado na figura 3.8, com um tempo de
execução superior ao arranque directo e apenas possível para binários de carga reduzidos, em
zonas de baixa velocidade. Nestes casos, recomenda-se quando:
4/17
Máquinas Eléctricas
Motores assíncronos
- haja que limitar a intensidade de arranque
- haja que realizar acelerações suaves
Arranque estrela – triângulo
Este tipo de arranque apenas pode ser realizado para motores com as seis extremidades das
bobines acessíveis e para os quais o modo de funcionamento normal seja em triângulo. O
arranque inicia-se com as fases do motor ligadas em estrela, estando assim, estas, submetidas à
tensão nominal sobre 3 . Como consequência desta redução de tensão:
ž em cada fase circula uma corrente que é 1 3 da corrente de arranque, à tensão nominal
ž a corrente de linha, em estrela, é igual à da fase
ž o motor, em situação normal, está ligado em triângulo, sendo a sua corrente de linha, 3
vezes a de fase. Assim, comparando com uma ligação directa em triângulo, o motor
ligado em estrela apenas absorve 1 / 3 / 3 = 1 / 3 da corrente de arranque – idem para
qualquer outro valor de escorregamento diferente do de arranque
ž o binário reduz-se, em função do quadrado da tensão de alimentação, pelo que, na
ligação em estrela, o binário se reduz de (1 / 3 ) 2 = 1 / 3 , quando comparado com o binário
produzido com o motor ligado em triângulo
Vê-se, assim, que o binário e a corrente
absorvida pelo motor, baixam na mesma proporção,
pelo que, o índice de arranque (Nm/kVA) se
mantém. Este método é semelhante ao de arranque
por auto-transformador, mas com uma relação de
transformação fixa de
É um método adequado para motores que
accionam cargas de baixo binário resistente, em
zona de baixas velocidades (caso de bombas e
ventiladores). A sua vantagem principal é a sua
simplicidade, pois basta um contactor adicional e
um temporizador para realizar a comutação, tal
como pode ser visto na figura 3.9.
1
3
Pode suceder que o binário de carga tenha
Figura 3.9
uma certa importância e que, por isso, a máquina
não acelere devidamente, realizando-se a comutação com altos escorregamentos e produzindo-se
picos de corrente e de binário, que invalidam este tipo de arranque. Na figura 3.10 pode ver-se
Figura 3.10
claramente este caso (figura à direita) comparado com o caso de uma comutação realizada à
velocidade correcta.
5/17
Máquinas Eléctricas
Motores assíncronos
No caso da comutação Y – ∆, surgem descontinudades na corrente que circula nas fases do
motor, pois estas são interrompidas3 quando se abre a estrela e, posteriormente, se fecha o
triângulo. Como os enrolamentos das fases do motor têm uma auto indução importante, as
correntes transitórias podem alcançar valores elevados. Devido a este factos, no caso de
comutação Y – ∆, em motores de média e grande potência, adoptam-se as seguintes variantes:
ž Y – ∆, com transição temporizada. Apropriado para binários de carga pequenos, com
inércia importante, de forma a que, durante a transição, se impede uma desaceleração
apreciável.
ž Arranque em 3 tempos
• estrela
• triângulo + resistência
• triângulo
O corte de corrente permanece, mas insere-se uma resistência, em série com as
fases, durante 2 a 5 segundos, para amortecer os transitórios.
ž Arranque Y – ∆, sem corte. As resistências limitadoras dos transitórios, para a etapa
triângulo, ligam-se antes de abrir a estrela.
Arranque por motor de várias velocidades
Sabe-se que a energia dissipada, no rotor, durante o arranque, é dado por:
Erot = 1 ⋅ ω02 ⋅ J
2
no caso, ideal, de binário de carga nulo.
Esta energia é absorvida pelo motor, da
rede de alimentação. Além disso, os
componentes rotativos do sistema de
accionamento completo, armazenam a energia
cinética:
E cin = 1 ⋅ ω 02 ⋅ J
2
Figura 3.11
Nesta hipótese de binário resistente nulo, o motor não realiza trabalho útil sobre a máquina
accionada, durante a fase de arranque. Sendo assim, a energia total absorvida da rede é:
Etot = Ecin + Erot = J ⋅ ω 02
A energia cinética não se dissipa em calor e, enquanto o sistema rodar, este armazena-a na
inércia, estando, teoricamente, disponível. Esta energia armazenada, dissipa-se no travão
mecânico ou electromagnético, quando se procede à travagem do motor.
3
Notar que, se a abertura dos contactos que ligam os enrolamentos em estrela, fosse realizada em simultâneo com o fecho
dos contactos que ligam os enrolamentos em triângulo, teríamos um instante de tempo em que as fases estariam curto
circuitadas. Daí a necessidade de se abrir, num primeiro instante, a estrela, e fechar, num instante imediatamente posterior,
o triângulo.
6/17
Máquinas Eléctricas
Motores assíncronos
Restringindo, agora, o estudo deste tipo de arranque à energia dissipada no rotor (Erot ) e
supondo que o motor tem duas velocidades – ω/2 e ω − o arranque far-se-á em duas etapas:
desde 0 até ω/2 e de ω/2 a ω.
A energia rotórica que se dissipa nas duas etapas, é:
þ gaiola de baixa velocidade – desde escorregamento (para esta gaiola ) g = 1 até g = 0,
em que ω0 = ω/2:
1
'
Erot
g 2 ω 2
ω2
1
⋅ J ⋅ = ⋅ J ⋅ − 0 = J ⋅
8
2
2 0 2
= ω 02
þ gaiola de alta velocidade – desde escorregamento (para esta gaiola ) g = ½ até g = 0,
em que ω0 = ω:
1
''
E rot
=
ω 02
g 2 2
ω2
1
⋅ J ⋅ = ω 2 ⋅ J ⋅ − 0 = J ⋅
8
8
2 0
Somando os dois termos:
'
''
Erot = Erot
+ Erot
=J⋅
ω2
4
observa-se que, mediante esta transição por gaiola de baixa velocidade (2P pólos) e
seguidamente por gaiola de alta velocidade (P pólos)4 , apenas se dissipa metade da energia que
se dissiparia com um motor de gaiola única, de alta velocidade. Assim a poupança energética é
de J ⋅ ω 2
, por cada arranque executado. Este tipo de motores, não são muito mais caros que
4
os de velocidade
única e apenas requerem um contactor adicional. Empregam-se em elevadores.
Arranque por motor auxiliar
Arranque realizado, acoplando, mecanicamente, ao motor principal um motor auxiliar, com
1 par de pólos a menos que aquele. Este motor auxiliar é projectado em função dos seguintes
aspectos:
Æ apenas funcionando na fase de arranque, o seu dimensionamento é ajustado do ponto de
vista do aquecimento (arranque ⇒ correntes elevadas ⇒ aquecimento)
Æ interessa fundamentalmente o binário produzido e não o seu rendimento
Arranque por enrolamento quebrado
Arranque por enrolamento parcial
4
Relembrar que a velocidade de rotação de um motor assíncrono é dada por: (frequência x 60)/nº_de_pares_pólos
7/17
Máquinas Eléctricas
Motores assíncronos
Rotor bobinado
Há casos, na industria, em que as elevadas correntes de arranque são inadmissíveis, bem como as
grandes reduções de binário. Nos motores de gaiola, para escorregamentos superiores a gmax –
escorregamento que define o ponto em que surge o binário máximo – a corrente absorvida aumenta de
forma drástica, acompanhada por uma forte redução de binário.
É sabido que o binário e a corrente absorvida, dependem da resistência do circuito do rotor. A
existência de um rotor bobinado e de escovas e segmentos torna o motor mais caro e de manutenção
mais delicada. No entanto, permitem que sejam alteradas as suas características internas (rotor), a
partir do exterior. Além disso, quando as resistências externas adicionadas têm valor muito superior às
resistências dos enrolamentos, a energia perdida no circuito rotórico dissipa-se, na sua maior parte,
nessas resistências externas, tornando a refrigeração mais fácil.
Durante os regimes de baixa velocidade (alto escorregamento) o motor é muito mais resistivo e,
portanto, mais eficaz na produção de binário para uma dada corrente. Assim, o motor de rotor
bobinado continua a ser a única solução, para arranques com elevada exigência de binário e elevada
inércia, bem como uma solução adequada, quando a rede de alimentação é de baixa capacidade, não
suportando correntes de arranque elevadas.
Muitas vezes, paradigmaticamente, um motor de rotor bobinado bem estudado, constitui uma
solução mais atractiva que um motor de gaiola, excessivamente sobredimensionado para vencer os
requisitos de arranque. Também nos casos de frequência elevada de arranques, com a correspondente
elevação de temperatura, havendo hipótese de colocar a maior parte da resistência do rotor no exterior,
consegue-se uma maior eficácia no arrefecimento do motor. Por último, a inserção de resistências
externas, de valor elevado, amortece os pares harmónicos pulsantes.
Arranque por resistência rotórica
O motor trabalha na zona linear da curva de binário. A equação seguinte é válida:
T
binário máximo Tmax = k.T
R1
com:
R3
R4
d3
d4
binário T
d0
binário nominal TN
escorregamento inicial d0
gN o escorregamento de binário nominal
g’ o escorregamento desejado
R2 a resistência rotórica
R’ext a resistência externa adicional
R2
d1
d2
tural
ca na
terísti
carac
'
g'
R2 + Rext
=
gN
R2
dn
dN
De acordo com a figura 3.12,
ω
calcular-se-ão
as
resistências
Figura 3.12
adequadas para:
o obter o nº de escalões adequado
o manter dentro de certos limites, o salto de binário, quando se faz a comutação (retira Rext )
Na figura 3.13 mostra-se o circuito de potência, para comando da desinserção (curto
circuito consecutivo de 2 escalões) das resistências rotóricas.
No anexo C é dado um exemplo de cálculo das resistências externas adicionais. As
expressões consideradas são as seguintes:
8/17
Máquinas Eléctricas
g0
g1 =
g2 =
Motores assíncronos
k
g1
g0
k =
k2
.
.
.
gn =
gN =
g0
k ( nescal +1)
g n ⋅ TN
T
1
g0
( nescal +1)
gN
k =
T
TN
n escal
− log T
log g 0
T
g N
N
=
−1
log (k )
Figura 3.13
R1 g1
=
−1
R gN
R2 g 2
=
−1
R gN
.
.
.
Rn− 1 g n −1
=
−1
Rn
gn
T
K.T
n escal
TN
gN
g0
g 1,2,3
gn
R1,2,3
R
– binário motor durante o arranque
– binário máximo, durante o arranque (define a oscilação)
– número de escalões
– binário nominal
– escorregamento nominal
– escorregamento inicial
– escorregamentos sucessivos
– escorregamento sobre a curva de binário natural
– resistências externas
– resistência rotórica
9/17
Máquinas Eléctricas
Motores assíncronos
Electromecânicos
A ligação do motor à carga é realizada através de equipamento com algumas propriedades
especiais. O denominador comum, aqui, é que o motor arranca directamente ligado à rede e, como a
carga está ligada ao motor através de um elemento mecânico, o arranque pode considerar-se em vazio,
isto é, o binário resistente é muito reduzido (praticamente nulo) e com inércia desprezável. Uma vez o
motor lançado, a carga é adicionada ao motor através deste sistema de acoplamento.
Acoplamento centrífugo
Este tipo de ligação motor-carga – figura 3.14 – tem
vantagens adicionais, tais como:
ž o arranque da máquina accionada realiza-se quando
o binário motor está no seu máximo
ž não há choques nem vibrações de torção no eixo do
motor
ž bom comportamento face a sobrecargas
ž praticamente sem perdas em serviço normal
(nominal), pois o acoplamento faz-se em zona de
baixo escorregamento
ž auto controlável
Figura 3.14
Acoplamento hidráulico
Este tipo de acoplamento é constituído por dois elementos de transmissão de potência (impulsor
e rotor impulsionado). Ambos têm paletas radiais e estão colocados dentro de uma carcaça com um
fluido hidráulico (óleo) que transmite a potência mecânica. O impulsor, que recebe a potência do
motor, actua como uma bomba centrífuga e cria uma corrente de fluido, sob pressão, que passa através
do rotor impulsionado e o arrasta. Este acoplamento tem a característica de não ser rígido, logo haverá
escorregamento entre eles. O escorregamento é uma medida da potência perdida no acoplamento. Se
tivermos:
ω1 - velocidade do eixo impulsor
ω2 - velocidade do eixo conduzido
Tt - binário transmitido
então (ω1 – ω2 ) será o escorregamento, e:
P1 = Tω1
P2 = Tω2
é a potência de entrada
é a potência de saída
As perdas de potência vêm:
Pp = P1 – P2 = T(ω1 – ω2 )
que expressas em percentagem:
Pp (%) = 100 ⋅
Pp
P1
= 100 ⋅
T ⋅ (ω1 − ω 2 )
ω −ω 2
= 100 ⋅ 1
=g
T ⋅ ω1
ω1
10/17
Máquinas Eléctricas
Motores assíncronos
Nas primeiras fases do arranque, o impulsor acelera rapidamente, ao passo que o rotor
impulsionado permanece parado, até que a velocidade do impulsionador seja suficiente para criar uma
pressão hidrodinâmica adequada à transmissão do binário. Neste momento, o motor já adquiriu uma
certa velocidade, pelo que, a corrente absorvida já baixou e o binário motor é suficiente.
Acoplamento electromagnético
Neste caso, o acoplamento é realizado por
intermédio de fricção entre dois discos, mas em que a
força que origina esta fricção é de origem
electromagnética. A forma de utilização é análoga à do
acoplamento centrífugo.
Figura 3.15
11/17
Máquinas Eléctricas
Motores assíncronos
Electrónicos
A banalização – baixo custo –, a versatilidade e as potencialidades dos semicondutores de
potência actuais, junto com a possibilidade de preparar algoritmos de controle sofisticados, permitem o
surgimento de técnicas de controle de motores muito poderosas. Estes componentes, não tendo
componentes móveis, são apelidados de conversores estáticos e não devem ser confundidos com os
variadores de frequência. Estes últimos empregam-se fundamentalmente para aplicações de variação
de velocidade, embora possuam capacidades adicionais de controle do arranque.
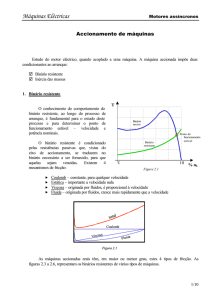
O arrancador estático
Um sistema de arranque correcto, é o que consegue que a corrente absorvida seja a estritamente
necessária para vencer o binário resistente e criar um binário excedente acelerador, capaz de vencer a
inércia do motor e da máquina accionada, num tempo
definido. Por exemplo, dado que um ventilador ou uma
T
bomba têm um binário resistente que cresce com o
Binário
quadrado da velocidade, teremos, nas primeiras fases
motor
do arranque, um excesso de binário motor (a vermelho,
na figura 3.16), sendo, evidentemente, possível arrancar
Binário
com valores de binário muito inferiores.
resistente
Na figura 3.17, vê-se o esquema de princípio de
um arrancador estático – cada fase da alimentação tem
um par de tirístores antiparalelos, sendo a tensão
%
Figura 3.16
aplicada (aos terminais do motor) função do ângulo de
disparo dos tirístores. Inicialmente, os tirístores são disparados com intervalos muito curtos, tendo
como efeito, um valor de tensão reduzido. O motor assíncrono modifica o binário e a corrente, em
função da tensão aplicada5 . À medida que
o arranque se processa, o sistema de
controle vai aumentando o ângulo de
disparo, mantendo a corrente dentro dos
limites definidos.
µP
comando
I
M
3
controle
§ Sinalização
§ Vigilâncias
§ Ajustes
~
Figura 3.17
5
Recorde-se que, o binário motor varia proporcionalmente ao quadrado da tensão eficaz e que a corrente absorvida é
proporcional à tensão eficaz
12/17
Máquinas Eléctricas
Motores assíncronos
Comparação económica de alternativas
O projecto de utilização de um sistema com accionamento por motor assíncrono, deve obedecer
a critérios técnicos (referidos anteriormente), legais, mas também a critérios económicos. Isto é, deve
ter-se a percepção de que o investimento realizado naqueles equipamentos foi amortizado (se “se
pagaram”), no fim da sua vida útil.
Nesta perspectiva, devem ponderar-se os seguintes custos:
Amortização do investimento
Esta análise deverá ser realizada tendo em vista o custo do dinheiro – taxas de juro – e a sua
depreciação ao longo do tempo – taxa de inflação – gasto para realizar aquele investimento, custo este
que é função da proporção entre recursos próprios e alheios (da empresa).
Custo da energia
No geral, o custo da energia gasta em qualquer um dos métodos de arranque, não é muito
diferente, pelo menos à escala do tempo considerado nas facturas. São mais importantes aspectos
como:
- diminuição da potência de ponta
- diminuição do valor da potência contratada
- possibilidade de aumentar a frequência de arranques, poupando, assim, as perdas relacionadas
com o funcionamento do motor em vazio(lastre e deslastre de cargas ligadas ao motor6 ).
Custos de manutenção
Aos custos dos equipamentos do sistema, dever-se-á adicionar, ainda, os custos de manutenção
preventiva ou preditiva, associados, incluindo o custo de mão de obra (própria ou contratada), os
consumíveis e outros custos de reparação que, por experiência, se conheçam.
Problemas associados ao arranque de motores, que implicam custos:
ž
ž
ž
ž
ž
ž
Fusão de fusíveis
Desgaste de contactos
Custo de stocks de peças para reparação
Disparo intempestivo de relés
Falhas em outros equipamentos, originados no arranque – transformadores
Duplicação de equipamentos, para evitar a interrupção da produção, durante as
reparações
ž Filtros, para atenuar os inconvenientes dos harmónicos (arrancadores electrónicos)
Custos produtivos
Análise das alternativas, em função dos efeitos do seu eventual mau funcionamento, no sistema
de produção da empresa.
O mais racional, é não avaliar as perdas de produção directa, mas apenas os custos de ter
equipamentos duplicados (para evitar paragens) e os tempos de substituição (do equipamento
duplicado).
Custos gerais
Espaço necessário, requerido pelas soluções alternativas.
Custos de instalação.
6
caso dos acoplamentos mecânicos e magnéticos
13/17
Máquinas Eléctricas
Motores assíncronos
Necessidade de pessoal próprio ou contratado.
Experiência com equipamentos semelhantes, já instalados.
Funções de protecção e de autodiagnóstico.
Registo de eventos.
14/17
Máquinas Eléctricas
Motores assíncronos
Anexo A
Gráficos para cálculo da redução de corrente e de binário, no momento do arranque, por inserção
de resistências estatóricas
1
0,9
I’a / I a
0,8
0,7
0,6
(R1+R’ 2)/(X1 +X’ 2) = 0,2
0,5
(R1+R’ 2)/(X1 +X’ 2) = 0,3
0,4
(R1+R’ 2)/(X1 +X’ 2) = 0,4
0,3
(R1+R’ 2)/(X1 +X’ 2) = 0,5
(R1+R’ 2)/(X1 +X’ 2) = 0,6
0,2
0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
5
5,5
6
Rad / (X1 + X’2)
1
0,8
Tad / T a
0,6
0,4
(R1+R’2 )/(X1+X’2 ) = 0,2
0,3
(R1+R’ 2)/(X1 +X’ 2) = 0,3
0
(R1+R’2 )/(X1+X’2 ) = 0,4
(R1+R’2 )/(X1+X’2 ) = 0,5
(R1+R’2 )/(X1+X’2 ) = 0,6
0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
5
5,5
6
Rad / (X1 + X’2)
15/17
Máquinas Eléctricas
Motores assíncronos
Anexo B
Um motor de rotor bobinado, deverá arrancar com um binário T/TN = 1,2. Tem um
escorregamento inicial de g0 = 1 e um escorregamento nominal de 2%. A oscilação de binário tolerada
é de k = 2. Determinar o nº de escalões, o deslizamento para cada comutação (curto circuito de cada
conjunto de resistências externas) e a relação Ri/R das resistências externas.
n escal
− log T
log g 0
T
g N
N
=
−1
log (k )
n escal =
( 0,02)− log (1,2) − 1 = 4,38
log 1
log (2 )
arredondando, teremos 5 escalões
1
1
g0
( nescal +1) 1
(5 +1)
gN
0
,
02
k =
=
= 1,86
T
1,2
TN
com uma oscilação de 1,86
g1 =
g0
k
...
R1 g1
=
−1
R gN
...
g0
g1
g2
g3
g4
g5
gn
1,0000
0,5371
0,2884
0,1549
0,0832
0,0447
0,0240
R1 /R
R2 /R
R3 /R
R4 /R
R5 /R
21,38
11,02
5,45
2,47
0,86
16/17
Máquinas Eléctricas
Motores assíncronos
Anexo C
Esforços mecânicos presente em acoplamentos de máquina a motores
Esforços externos
Esforços internos
• MT – momento tensor
• GA – peso do elemento de transmissão
• FR – força radial externa
• FA – força axial externa
• GR – peso próprio do rotor com eixo
• ZR – força radial de atracção magnética
• ZA – força axial de atracção magnética
•GV – peso do elemento externo no lado oposto ao accionamento
•GM – peso total do motor
Fig. 3.1 Principais esforços actuantes num motor
17/17