Tema 10_ Ângulos

ÂNGULOS
CONTEÚDOS

Ângulos

Classificação de um ângulo

Ângulos complementares e suplementares

Ângulos adjacentes

Bissetriz de um ângulo
AMPLIANDO SEUS CONHECIMENTOS
A ideia de ângulo está presente nas mais diversas situações. Imagine, por exemplo, que
em uma sala de aula, uma pessoa sentada mais próxima do centro dessa sala (ponto A) e
outras duas sentadas nas extremidades (pontos B e C). Cada uma delas têm um campo de
visão em relação a lousa.
B
A
C
Figura 1 – Sala de aula
Fonte: Microsoft Office
Da forma como estão posicionadas, é possível dizer que o melhor campo de visão é o da
pessoa que está mais ao centro, isso porque ela consegue visualizar melhor toda o
1
comprimento da lousa. Observe no esquema abaixo o suposto campo de visão de cada
uma dessas pessoas.
Observando as semirretas que indicam o
campo de visão de cada uma dessas
pessoas,
notamos
diferentes
aberturas,
que
essa
eles
têm
abertura
podemos identificar como ângulo.
Ângulo: Dada duas semirretas, que têm a mesma origem, chamamos de ângulo a
reunião dessas duas semirretas.
O
Os ponteiros de um relógio, ao marcar as horas e minutos, vão ao longo do dia formando
diversos ângulos. Observe o ângulo formado quando o relógio marca 12h10min, por
exemplo.
11
12 1
2
10
9
3
4
8
7
6
5
Figura 2 – Relógio
Fonte: Fundação Bradesco
2
Identificando o ângulo
O ângulo a seguir é identificado como ângulo AÔD . O ponto O é o vértice do ângulo e as
semirretas Oa e Od são os lados do ângulo.
a
d
Vértice
A medida de um ângulo é dada em relação a sua abertura. A unidade padrão utilizada
para essa medida é o grau e utiliza-se o símbolo ° após o número.
1° (1 grau) corresponde a
1
da circunferência.
360
1°
Figura 3
Fonte: Microsoft Office
3
Para medir um ângulo utiliza-se o instrumento chamado transferidor. Observe-o:
Figura 4 – Transferidor
Fonte: Fundação Bradesco
Cada tracinho do instrumento representa um grau. Medir um ângulo, significa ver quantas
vezes o valor unitário (grau) cabe em um ângulo.
Veja no transferidor a seguir, alguns ângulos e suas medidas:
C
AÔB  30
D
AÔC  80
B
AÔD  135
A
O
Figura 5 – Medida de ângulo
Fonte: Fundação Bradesco
4
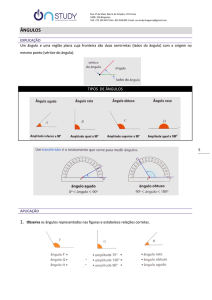
Alguns ângulos são identificados com uma nomenclatura específica, são eles: reto,
obtuso, agudo e raso.
Ângulo
reto:
sua
medida é igual a 90°
Ângulo obtuso: sua
medida é maior que 90°
Ângulo agudo: sua
medida é menor que
90°
Ângulo raso: sua medida é igual a 180°
Além dessas nomenclaturas, dados dois ângulos, esses podem ser classificados como
suplementares e complementares.
Os ângulos AÔB e BÔC são
complementares. Dois ângulos
são
considerados
complementares quando a soma
Os
ângulos
suplementares.
EÔF
Dois
e
FÔG
são
ângulos
são
considerados suplementares quando a
soma de suas medidas é igual a 180°.
de suas medidas é igual a 90°.
5
Ângulos consecutivos
Na figura observamos três ângulos, são eles:
AÔB, BÔC e AÔC. Comparando-os, dois a
dois temos:
AÔB e BÔC são consecutivos.
AÔB e AÔC são consecutivos.
BÔC e AÔC são consecutivos.
Dois ângulos são chamados de consecutivos quando possuem o mesmo vértice e tem um
lado em comum.
Em relação aos ângulos AÔB, BÔC e AÔC observa-se que:
AÔB e BÔC tem em comum o vértice O e o lado OB .
AÔB e AÔC tem em comum o vértice O e o lado OA .
BÔC e AÔC tem em comum o vértice O e o lado OC .
Ângulos Adjacentes
Na figura observamos três ângulos, são eles:
AÔB, BÔC e AÔC. Comparando-os temos:
AÔB e BÔC adjacentes.
Dois ângulos são chamados de adjacentes quando não possuem pontos internos em
comum.
6
Bissetriz de um ângulo
30°
30°
Dado o ângulo AÔC, ao traçar a semirreta OB com origem no ponto O, o ângulo foi
dividido em dois ângulos adjacentes de mesma medida.
A semirreta OB é identificada como bissetriz do ângulo AÔC.
ATIVIDADES
1.Considere um relógio de ponteiros, se ele está dividido em 12 partes, quando o ponteiro
das horas desloca-se da marcação de 2 horas para a marcação de 3 horas, qual foi ângulo
percorrido por ele?
11
12
1
11
2
10
9
4
7
6
5
1
2
10
3
8
12
9
3
4
8
7
6
5
7
2.Às 6 horas da manhã Ana saiu para ir trabalhar, a moça retornou do trabalho e observou
que o ponteiro das horas do relógio que fica em sua cozinha, já havia percorrido 300º. Que
horas eram quando a moça retornou do trabalho?
11
12
1
2
10
9
3
4
8
7
6
5
3. Leia as afirmativas e identifique como verdadeira (V) ou falsa (F).
a) ( ) Se um ângulo mede 130°, seu suplementar mede 50°.
b) ( ) Um ângulo de 35° é complementar a um ângulo de 55°.
c) ( ) Dado um ângulo de 120°, ao traçar sua bissetriz, obtêm-se dois ângulos consecutivos
sendo a medida de um deles igual a 100° e a medida do outro igual a 20°.
d) ( ) Um ângulo reto é maior que um ângulo obtuso.
e) ( ) Dois ângulos retos formam um ângulo raso.
4. Se o ângulo AÔD é um ângulo raso e a semirreta OB a bissetriz do ângulo AÔC, qual é
a medida do ângulo BÔC?
C
B
80°
D
O
A
8
5. (FUVEST/PASUSP - 2009) Segundo norma do Instituto Nacional de Metrologia,
Normalização e Qualidade Industrial (INMETRO), os ônibus urbanos devem ter os encostos
dos bancos fazendo um ângulo α com o assento horizontal compreendido entre 105° e
115°. Indique, entre os bancos abaixo, aquele que esteja em conformidade com essa
norma.
9
6. (ENEM - 2009) Rotas aéreas são como pontes que ligam cidades, estados ou países. O
mapa a seguir mostra os estados brasileiros e a localização de algumas capitais
identificadas pelos números. Considere que a direção seguida por um avião AI que partiu
de Brasília – DF, sem escalas, para Belém, no Pará, seja um segmento de reta com
extremidades em DF e em 4.
Suponha que um passageiro de nome Carlos pegou um avião AII, que seguiu a direção que
forma um ângulo de 135° graus no sentido horário com a rota Brasília – Belém e pousou
em alguma das capitais brasileiras. Ao desembarcar, Carlos fez uma conexão e embarcou
em um avião AIII, que seguiu a direção que forma um ângulo reto, no sentido anti-horário,
com a direção seguida pelo avião AII ao partir de Brasília-DF. Considerando que a direção
seguida por um avião é sempre dada pela semirreta com origem na cidade de partida e que
passa pela cidade destino do avião, pela descrição dada, o passageiro Carlos fez uma
conexão em
a) Belo Horizonte, e em seguida embarcou para Curitiba.
b) Belo Horizonte, e em seguida embarcou para Salvador.
c) Boa Vista, e em seguida embarcou para Porto Velho.
d) Goiânia, e em seguida embarcou para o Rio de Janeiro.
e) Goiânia, e em seguida embarcou para Manaus.
10
7. Sendo o ângulo BÔC suplementar do ângulo α, interno ao triângulo. Se o triângulo dado
é um triângulo equilátero, apresentando todos os seus ângulos medidas iguais, qual é a
medida de cada um deles?
120°
α
LEITURA COMPLEMENTAR
O grau é a unidade de medida mais utilizada para medir ângulos. Porém quando se fala
em medida angular de arco, é comum utilizar o radiano.
Medida em radianos: Seja POQ um ângulo com centro O, como na figura abaixo:
11
Se a circunferência tem raio r e o ângulo intercepta um arco de medida s, então o
quociente s/r será a medida do ângulo em radianos e dizemos que o ângulo mede s/r rad.
Exemplo: Encontre a medida em radianos do ângulo reto QOP
Solução: Desenhe uma circunferência de raio r e centro O.
Encontre a medida em radianos do ângulo reto QOP. A circunferência de raio r mede 2 r.
O ângulo reto corresponde à 1/4 da circunferência. Portanto o comprimento do ângulo reto s
é dado por:
e a medida em radianos por:
12
Transformação entre graus e radianos
Simplesmente, usamos a proporção abaixo:
Medida em graus Medida em radianos

180
π
Usando a expressão acima, temos a relação:
Medida em
graus
0
30
45
60
90
120
135
Medida em
radianos
0
/6
/4
/3
/2
2 /3
3 /4
150
180
240
270
360
5 /6
4 /3
3 /2
2
Disponível em: <http://www.mat.ufmg.br/protem/Teste/trig2/trig/trig0.html>. Acesso em: 18 maio. 2016.
12h25min.
INDICAÇÃO
Para estudar um pouco mais sobre os ângulos, faça a audição do podcast disponível na
Biblioteca Digital do Portal EJA. Você poderá acessá-lo no seguinte endereço:
http://www.eja.educacao.org.br/bibliotecadigital/cienciasnatureza1/podcasts/Lists/Podcast/
DispForm.aspx?ID=6&Source=http%3A%2F%2Fwww%2Eeja%2Eeducacao%2Eorg%2Eb
r%2Fbibliotecadigital%2Fcienciasnatureza1%2Fpodcasts%2FPaginas%2FPodcastEM%2
Easpx>.
No mesmo endereço eletrônico existe uma atividade relacionada ao podcast, não deixe de
realizá-la.
13
REFERÊNCIAS
FUVEST.
PASUSP
–
2009.
Disponível
em:
<http://www.fuvest.br/vest2010/provas/pasusp2009v.pdf>. Acesso em: 17 maio. 2016.
16h11min.
IEZZI, Gelson. MACHADO, Antonio.
DOCE, Osvaldo. Geometria Plana: Conceitos
básicos. 1ª ed. São Paulo: Atual, 2008. p. 9 – 11.
INEP.ENEM
–
2009.
Prova
azul.
Disponível
em:<
http://download.inep.gov.br/educacao_basica/enem/downloads/2009/dia2_caderno7.pdf>.
Acesso em: 17 maio. 2016. 16h.
MICROSOFT Office for Windows 2009. Version 7. [S.l.]: Microsoft Corporation, 2009. 1 CDROM.
SÃO PAULO (Estado). Secretaria da Educação (SEE). Educação de Jovens e Adultos:
Mundo do Trabalho modalidade semipresencial, v 1. Matemática: caderno do estudante.
Disponível
em:
<http://www.ejamundodotrabalho.sp.gov.br/ConteudoCEEJA.aspx?MateriaID=78&tipo=Alu
no>. Acesso em: 18 maio. 2016. 10h.
UFMG.
Trigonometria:
revisão.
Disponível
em:<
http://www.mat.ufmg.br/protem/Teste/trig2/trig/trig0.html>. Acesso em: 18 maio. 2016.
12h25min.
GABARITO
1.Se a circunferência está dividida em 12 partes, o ângulo percorrido pelo ponteiro das
horas durante 1 hora, é de 30°. Acompanhe:
360
 30
12
2. Se o espaço entre cada uma das divisões do relógio representa o deslocamento de um
ângulo de 30°, ao deslocar das 6 horas percorrendo um ângulo de 300° o ponteiro está
marcando 4h. Acompanhe:
14
300
 10.
30
Se já se passaram 10h, ele retornou para casa às 4h da tarde.
3. Leia as afirmativas e identifique como verdadeira (V) ou falsa (F).
a) ( V ) Se um ângulo mede 130°, seu suplementar mede 50°.
b) ( V ) Um ângulo de 35° é complementar a um ângulo de 55°.
c) ( F ) Dado um ângulo de 120°, ao traçar sua bissetriz, obtêm-se dois ângulos
consecutivos sendo a medida de um deles igual a 100° e a medida do outro igual a 20°.
d) ( F ) Um ângulo reto é maior que um ângulo obtuso.
e) ( V ) Dois ângulos retos formam um ângulo raso.
4. Sendo AÔD um ângulo raso, a soma do ângulo AÔC com o ângulo CÔD é igual a 180°.
Se CÔD mede 80º, AÔC mede 100°. Sabe-se que a bissetriz de um ângulo divide esse
ângulo em dois ângulos congruentes, logo BÔC mede 50°.
5. Alternativa correta é a letra c.
O ângulo α deve ser:
105° < α< 115°
Considerando α igual a 115°, temos:
180 – 115° = 65°
Considerando α igual a 105°, temos:
180° – 105° = 75°
Portanto, o suplementar de α deverá apresentar medida maior que 65° e menor que 75°.
6. A alternativa correta é a letra B.
O primeiro avião que Carlos pegou, seguiu a direção que forma um ângulo de 135° graus
no sentido horário com a rota de Brasília, assim temos:
15
Direção aproximada seguida por AIII
Direção aproximada seguida por AII
7. Sendo o ângulo BÔC suplementar ao ângulo α, conclui-se que o ângulo α apresenta
medida igual a 60°.Acompanhe:
120° + α = 180°
α = 180° - 120°
α = 60°
Se todos os ângulos desse triângulo são congruentes, cada um deles têm 60°.
16