c - UFRGS

ENG04030 ANÁLISE DE CIRCUITOS I . PROVA 1 2007/1 30/04/2007
1) (6 pontos)
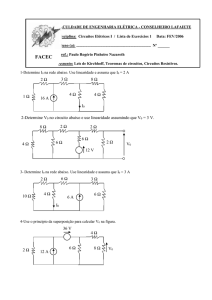
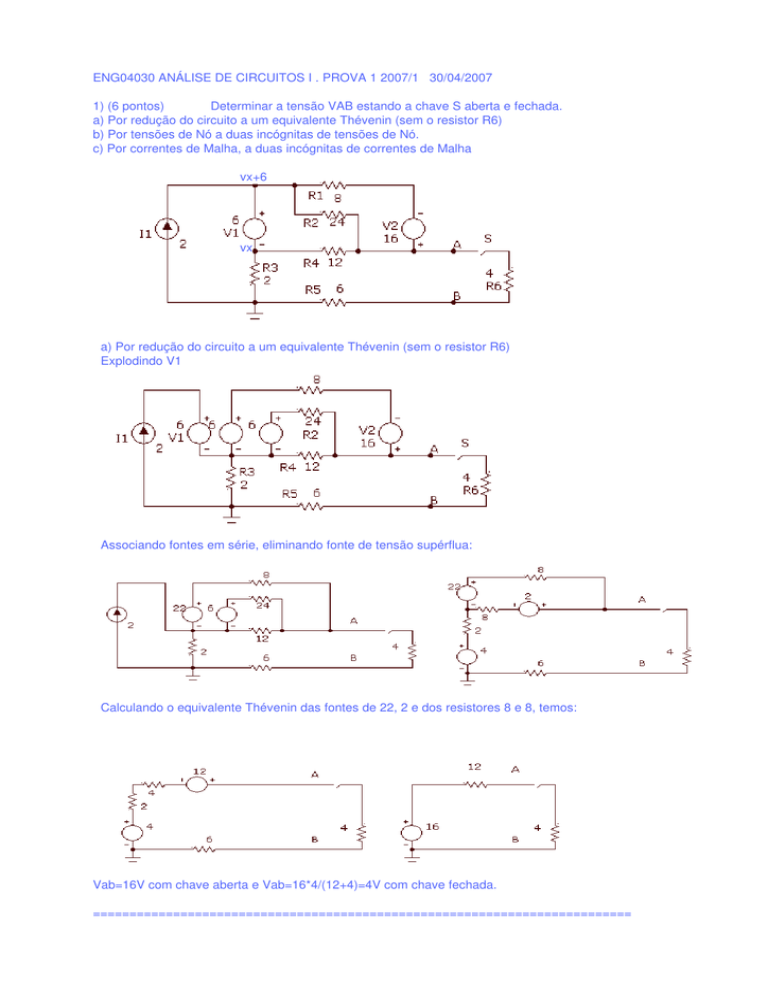
Determinar a tensão VAB estando a chave S aberta e fechada.
a) Por redução do circuito a um equivalente Thévenin (sem o resistor R6)
b) Por tensões de Nó a duas incógnitas de tensões de Nó.
c) Por correntes de Malha, a duas incógnitas de correntes de Malha
vx+6
vx
a) Por redução do circuito a um equivalente Thévenin (sem o resistor R6)
Explodindo V1
Associando fontes em série, eliminando fonte de tensão supérflua:
Calculando o equivalente Thévenin das fontes de 22, 2 e dos resistores 8 e 8, temos:
Vab=16V com chave aberta e Vab=16*4/(12+4)=4V com chave fechada.
==========================================================================
b) Por tensões de Nó a duas incógnitas de tensões de Nó.
vx
vx
2
va
vx
6
12
va
R6
va
vx
6
24
va
6
vx
va
16
va
8
vx
12
6
16
8
va
vx
2 0
6
3
va
0
24
1.
vx
( R6
1.
6)
4
va
6
3
va
8
3
0
8
va( R6 )
3.
1
( R6
1
6)
8
va( 4 ) = 10
va 10
= 16
6
Com a chave aberta, R6=100 milhões de ohms, por exemplo, a tensão Vab=va =16V
Com a chave fechada, R6=4, a tensão va é 10V e a tensão vab é queda sobre 4 ohms ou seja 4V.
va( 4 ) . 4
4
6
=4
=============================================================================
c) Por correntes de Malha, a duas incógnitas de correntes de Malha.
Para isto devemos reduzir uma malha do circuito, por exemplo, reduzindo R2, R3 e V2 à um Thevenin:
Vth
16. 24
8
Vth = 12
24
1
Rth
1
1
24
8
Rth = 6
Equações de corrente de malha ia e ib,considerando R6 (chave fechada). Naturalmente, se fizéssemos
análise com chave aberta, não precisaríamos da redução do circuito, pois só teríamos duas malhas de
corrente de malha desconhecida. Mas assim fazemos uma análise apenas:
2.
ia. ( 6 12 ) 12 6 ib. 12 0
ia 1
ib
3
ib. ( 2
12
R6
6)
A tensão Vab= ib*R6
4
ia. 12 0
ib. ( 20
R6 )
ib 10
Com chave aberta (R6=100 megohms)
Com chave fechada (R6=4 ohms)
8
16
8. ib 0
= 1.6 10
7
ib( R6 )
16
( 12
R6 )
ib( 4 ) = 1
8
8
ib 10 . 10 = 16
ib( 4 ) . 4 = 4
Confirmado. Vab=16V, com chave aberta e Vab=4V, com chave fechada.
=========================================================================
=========================================================================
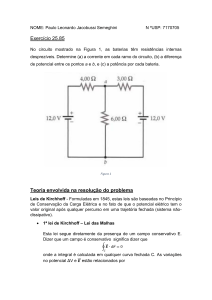
2)( 4 pontos) Determine o equivalente Thevenin do circuito, entre pontos A e B:
Novamente, podemos calcular a tensão a circuito aberto e a corrente a curto circuito, colocando um curto
entre A e B. Calculando a tensão no nó A, temos a tensão a circuito aberto. E calculado o somatório das
correntes no nó A, teremos isc.
Eliminamos os supérfluos para o cálculo de va. São os dois resistores em série com a fonte de
corrente de 2A, e todos os componentes (3 resistores e uma fonte de corrente) em paralelo com a fonte
de tensão de 12V.
Também descobrimos que uma ponte equilibrada está presente no circuito, pois 2*6=6*2, e sua
resistência equivalente vale 12//4=3 ohms.
Ficamos com apenas um nó essencial desconhecido, ou seja, va.
va
12
4
va
12
va
3
2. ( va
12 )
12
2 0
Colocando um curto entre A e B, com corrente isc de A para B, o somatório das correntes no nó A
deve ser nulo (Lei de Kirchhoff).
Esta é a tensão de Thévenin
va 14
2
12
12
2 . ( 12 )
4
3
12
isc 0
isc
7
Rth
va
isc
Rth = 2
Esta é a resistência de
Thévenin.