apostila 2 - teoria da computação – tutporia - UEG

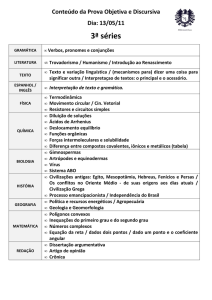
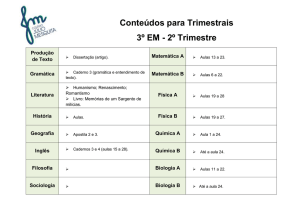
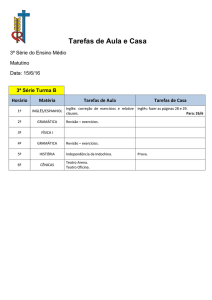
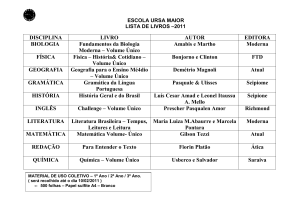
APOSTILA 2 - TEORIA DA COMPUTAÇÃO – TUTPORIA
LINGUAGENS LIVRES-DO-CONTEXTO
Gramáticas livres-do-contexto foram primeiramente usadas no estudo de
linguagens humanas. Uma maneira de entender o relacionamento de termos
como nome, verbo, e preposição e suas respectivas frases leva a uma recursão
natural porque frases nominais podem aparecer dentro de frases verbais e viceversa. Gramáticas livres-do-contexto podem capturar aspectos importantes
desses relacionamentos.
Uma aplicação importante de gramáticas livres-de-contexto ocorre na
especificação e compilação de linguagens de programação. Uma gramática para
uma linguagem de programação frequentemente aparece como uma referência
para pessoas que estão tentando aprender a sintaxe da linguagem. Projetistas
de
compiladores
e
interpretadores
para
linguagens
de
programação
frequemente começam obtendo uma gramática para a linguagem.
A maioria dos compiladores e interpretadores contém uma componente
chamada de analisador que extrai o significado de um programa antes de gerar
o código compilado ou realizar a execução¸˜ao interpretada.
Um número de metodologias facilita a construção de um analisador uma vez que
uma gramática livre-do-contexto está disponível. Algumas ferramentas até
geram automaticamente o analisador a partir da gramática.
A coleção de linguagens associadas a gramáticas livres-do-contexto são
chamadas as linguagens livres-do-contexto. Elas incluem todas as linguagens
regulares e muitas linguagens adicionais.
GRAMÁTICAS LIVRES-DO-CONTEXTO
O que segue é um exemplo de uma gramática livre-do-contexto, que
chamaremos G1.
Uma gramática consiste de uma coleção de regras de substituição, também
chamadas produções. Cada regra aparece como uma linha na gramática e
compreende um símbolo e uma cadeia, separados por uma seta. O símbolo e
chamado uma variável.
A cadeia consiste de variáveis e outros símbolos chamados terminais. Os
símbolos variáveis são frequentemente representados por letras maiúsculas. Os
terminais são análogos ao alfabeto de entrada e frequentemente são
representados por letras minúsculas, números, ou símbolos especiais. Uma
variável ´e designada a variável inicial. Ela usualmente ocorre no lado esquerdo
de uma das primeiras regras da gramatica.
Você usa uma gramática para descrever uma linguagem gerando cada cadeia
daquela linguagem da seguinte maneira:
1. Escreva a variável inicial. Ela é a variável no lado esquerdo da primeira
regra, a menos que seja especificado o contrário.
2. Encontre uma variável que está escrita e uma regra que começa com
aquela Variável. Substitua a variável escrita pelo lado direito daquela
regra.
3. Repita o passo 2 até que nenhuma variável permaneça.
Por exemplo, a gramática G1 gera a cadeia 000#111. A sequência de
substituições para obter uma cadeia é chamada uma derivação. Uma derivação
da cadeia 000#111 na gramática G1 é
Você pode também representar a mesma informação de uma maneira mais
pictórica usando uma árvore sintática.
DEFINIÇÃO FORMAL DE UMA GRAMÁTICA LIVRE-DO-CONTEXTO
_______________________________________________________________
PROGRAMA
Conjunto de operações e testes compostos de acordo com uma estrutura de
controle. O tipo de estrutura de controle associada determina uma classificação
de programas como:
Monolítico
Iterativo
Recursivo
 Estruturação Monolítica
É baseada em desvios condicionais e incondicionais, não possuindo
mecanismos explícitos de iteração, subdivisão ou recursão.
 Estruturação Iterativa
Possui mecanismos de controle de iterações de trechos de programas.
 Estruturação Recursiva
Possui mecanismos de estruturação em subrotinas recursivas.
COMPOSIÇÃO DAS INSTRUÇÕES
Sequencial:
A execução da operação ou teste subsequente somente pode ser realizada após
o encerramento da execução da operação ou teste anterior.
Não Determinista:
Uma das operações (ou testes) compostas é escolhida para ser executada.
Composição Concorrente:
As operações ou testes compostos podem ser executados em qualquer ordem,
inclusive simultaneamente, ou seja, a ordem de execução é irrelevante.
Instruções – Operações e Testes
Não é necessário saber qual a natureza precisa das operações e dos testes que
constituem as instruções.

Identificadores de Operações: F, G, H, ...

Identificadores de Testes: T1, T2, T3, ...
Um teste é uma operação de um tipo especial a qual produz somente um dos
dois possíveis valores verdade, ou seja, verdadeiro ou falso
Uma operação que não faz coisa alguma, denominada: operação vazia,
denotada pelo símbolo
.
PROGRAMA MONOLÍTICO
É estruturado, usando desvios condicionais e incondicionais, não fazendo uso
explícito de mecanismos auxiliares de programação. A lógica é distribuída por
todo o bloco (monólito) que constitui o programa.
FLUXOGRAMAS
É uma das formas mais comuns de especificar programas monolíticos
Rótulo: ou Etiqueta é uma cadeia de caracteres finita constituída de letras ou
dígitos.
Instrução rotulada: é uma sequência de símbolos de uma das duas formas a
seguir:
 Operação r1: faça F vá_para r2 ou r1: faça vá_para r2
 Teste r1: se T então vá_para r2 senão vá_para r3
Instruções rotuladas:
MÁQUINAS
O objetivo de uma máquina é suprir todas as informações necessárias para que
a computação de um programa possa ser descrita. Cabe a máquina suprir o
significado (semântica) aos identificadores das instruções e testes.
Cada identificador de operação e de teste interpretado pela máquina deve ser
associado a uma transformação na estrutura de memória e a uma função
verdade, respectivamente.
Nem todo o identificador de operação ou teste é definido em uma máquina;Para
cada identificador de operação ou teste definido em uma máquina, existe
somente uma função associada;
A máquina deve descrever o armazenamento ou recuperação de informação
na estrutura de memória. Uma Máquina é uma 7-upla:
COMPUTAÇÃO
Uma computação de um programa monolítico é um histórico de instruções
executadas e o correspondente valor de memória. O histórico é representado na
forma de uma cadeia de pares onde:
 Cada par reflete um estado da máquina para o programa (instrução a ser
executada e valor de memória).
 A cadeia reflete uma sequência de estados possíveis a partir do estado
inicial (instrução inicial e valor de memória).
Computação pode ser Finita ou Infinita:
 Um teste e operação vazia não alteram o valor corrente da memória;
 Em uma computação infinita, rótulo algum da cadeia é final.
EQUIVALÊNCIA DE PROGRAMAS E MÁQUINAS
 Relação Equivalência Forte de Programas:
Um par de programas pertence a relação se as correspondentes funções
computadas coincidem para qualquer máquina.
Sejam P e Q dois programas arbitrários, não necessariamente do mesmo tipo.
Então o par (P, Q) está na Relação Equivalência Forte de Programas, denotada
por: P ≡ Q se, e somente se, para qualquer máquina M, as correspondentes
funções parciais computadas são iguais, ⟨P, M⟩ = ⟨Q, M⟩.
Neste caso, P e Q são ditos Programas Equivalentes Fortemente.
 Relação Equivalência de Programas em uma Máquina:
Um par de programas pertence a relação se as correspondentes funções
computadas coincidem para uma dada máquina.
 Relação Equivalência de Máquinas:
Um par de máquinas pertence a relação se as máquinas podem se simular
mutuamente. A simulação de uma máquina por outra pode ser feita usando
programas diferentes.
Referência
DIVERIO, T. A.; MENEZES, P. B. Teoria da Computação: Máquinas Universais e
Computabilidade, Série Livros Didáticos Número 5, Instituto de Informática, da UFRGS,
Editora Sagra Luzzatto, 1a edição, 1999.
SILVA, Rômulo. Teoria da Computação. 2007
_______________________________________________________________
TRABALHO SOBRE TEORIA DA COMPUTABILIDADE
Enviar por email: [email protected]
Data de entrega: até 26/06
LISTA DE EXERCÍCIO – ENTREGA ATÉ 26/06