instruções para a elaboração da versão final a ser

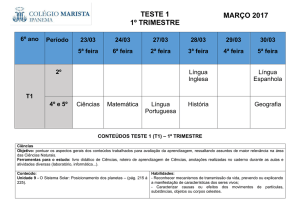
VII SECITEC - SEMANA DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA
Metodologia do Processo de Mudança de Base de um Sistema de
Numeração e sua Aplicação Computacional
Pablo Vandré Jacob Furlan - [email protected]
IFG/Formosa
Mário Teixeira Lemes - [email protected]
IFG/Formosa
Ana Lívia Félix e Silva - [email protected]
IFG/Formosa
Resumo
O sistema de numeração mais utilizado hoje é o sistema de numeração decimal, este sistema é o
ensinado em todas as escolas de educação básica como o sistema básico e, em geral, não se é
mostrado outros sistemas de numeração, com exceção do sistema de numeração romano. Neste
trabalho mostraremos que existem outros sistemas de numeração tão simples quanto o sistema
decimal. Alguns outros sistemas já foram utilizados no decorrer da história, um exemplo citado no
texto se deve aos babilônios que usavam o sistema de numeração sexagesimal. Hoje em dia, os
computadores são um dos exemplos mais comum de uso de outro sistema de numeração que não o
sistema de numeração decimal.
Palavras-Chave
Sistema Decimal, Sistema Binário, informática
O que é um Sistema de Numeração
Quando trabalhamos com números naturais na forma escrita, seja para
fazermos contas, seja para associar quantidade de objetos em um conjunto,
utilizamos um conjunto com dez símbolos, que vão do zero ao nove (0,1,2,...,9) e
que ficam dispostos em uma ordem pré-determinada. Para cada ordem distinta que
colocamos estes símbolos eles representarão um número diferente.
Esta forma de representar os números é chamada de sistema de numeração
decimal, pois usamos apenas dez símbolos para representar todos os números.
1
VII SECITEC - SEMANA DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA
Outra forma de se representar os números é por algarismos romanos, que, num
primeiro estudo não se parece tão intuitivo.
Mas será que existe outro sistema de numeração que se pareça com o
sistema de numeração decimal? Se existir quantos símbolos este novo sistema deve
possuir? Qual razão de priorizarmos o sistema de numeração decimal?
A razão mais aceita para usarmos o sistema de numeração decimal é que
temos dez dedos nas mãos. Isto facilitaria as contas, associando cada símbolo com
um dedo da mão e assim temos uma forma quase intuitiva de contar uma
quantidade pequena de objetos, e ate mesmo fazer pequenas contas.
Na verdade, existem infinitas formas de se representar os números naturais
baseadas na quantidade de símbolos que temos para representá-los. Sempre que
tivermos mais que dois símbolos, podemos criar um sistema de numeração.
Os babilônios usavam o sistema sexagesimal e devemos a eles dividir o dia
em vinte e quatro horas ou os ângulos de um círculo baseado no tamanho total de
360 graus.
Neste trabalho veremos que o uso de outro sistema de numeração é
amplamente utilizado hoje em dia, nos nossos computadores pessoais, já que estes
não “enxergam” o mundo (e os números) como nós.
Sistema de Numeração
Para entender como funcionam estes outros métodos de representar os
números precisamos primeiramente entender como funciona o sistema de
numeração decimal. Note que ao representarmos os números naturais, após os
noves primeiros números (sem contar o zero), acrescentamos outra “casa” para
representar o próximo número e assim conseguimos representar todos os números
até o número noventa e nove, onde, novamente acrescentamos outra casa e agora
podemos trabalhar com três símbolos para representar os próximos números.
2
VII SECITEC - SEMANA DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA
Assim, dado um número qualquer, quando queremos representar ele no
sistema de numeração decimal devemos primeiramente descobrir qual a maior
potência de dez que o divide, suponha que seja a n-ésima, então o número
necessita de n casas para ser representado e a primeira delas é a parte inteira
dessa divisão. O resto da divisão do número pela n-ésima potência de dez deve ser
dividido pela (n-1)-ésima potência de dez e a segunda casa da representação do
número é a parte inteira dessa divisão, e assim por diante, até a divisão por 1, que é
dez elevado a zero, e fica na n-ésima casa da representação. Por exemplo:
(Dois mil quinhentos e trinta e dois)= 2*10³ + 5*10² + 3*10¹ + 2*1 = (2532) 10
Quando usamos outro sistema de numeração com m símbolos, diremos que a
base deste sistema de numeração é m, assim o sistema de numeração decimal tem
base 10 e quando mudamos este sistema de numeração dizemos apenas que
mudamos sua base. Os outros sistemas seguem a mesma lógica do sistema de
numeração decimal, por exemplo, se fossemos escrever dois mil quinhentos e trinta
e dois na base oito, primeiramente teríamos apenas oito símbolos (0,1,2,3,4,5,6,7), o
oito neste caso seria representado por 10 1, que é a primeira representação que
precisa usar duas casas, e então teríamos:
(Dois mil quinhentos e trinta e dois)=4*10³+7*10²+4*10+4=(4744) 8
Tipos de Conversão
Decimal para Binário:
Para realizar conversões de base podemos também utilizar outros tipos de
métodos, por exemplo, o método de divisão repetida. Por este método a conversão
do número em sua representação em decimal (número) 10 para binário (número) 2
torna-se mais simples, deve-se apenas adotar os seguintes passos:
 Dividir o número decimal por dois. Caso o resultado seja exato, aquela divisão
terá resto zero, se não for exato terá resto um.
1
Note que o número oito é representado pelo símbolo 10 pois no conjunto com apenas oito símbolos, começando pelo zero,
exaurimos todas as possibilidades de representação antes de contarmos oito.
3
VII SECITEC - SEMANA DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA

Deve-se, então, dividir o quociente da divisão anterior novamente por dois e
repetir este processo até que o quociente da divisão seja igual a 0 zero.
 O número em binário corresponde aos restos obtidos em sua ordem inversa.
Note na Tabela 1 os valores de quociente e resto para a transformação de
número em decimal para sua representação binária.
Tabela 1- Transformação do número decimal (1985)10 para binário
Ordem
Divisão
Quociente
1
1985/2
992
2
992/2
496
3
496/2
248
4
248/2
124
5
124/2
62
6
62/2
31
7
31/2
15
8
15/2
7
9
7/2
3
10
3/2
1
11
1/2
0
Resto
1
0
0
0
0
0
1
1
1
1
1
Assim, conclui-se que: (1985)10 = (11111000001)2
Base Binária e sua Aplicabilidade em Computação
O sistema binário é o sistema de numeração utilizado pelos computadores devido sua fácil representação nos circuitos eletrônicos: 0 - ausência de corrente elétrica e 1 - presença de corrente (está convenção é chamada de lógica positiva, se a
convenção for invertida, ou seja, 0 - presença de corrente e 1 - ausência, então temos a chamada lógica negativa).
Referências
1. Gonick, Larry (1984). Introdução Ilustrada à Computação (São Paulo: Harper
& Row do Brasil).
2. Bianchi, Paulo; Bezerra, Milton (1983). Microcomputadores. ArquiteturaProjeto-Programação (Rio de Janeiro: LTC).
3. Murdocca, Miles J.; Heuring, Vincent P (2000). Introdução à Arquitetura de
Computadores (Rio de Janeiro: Campus).
4. Davis, Martin (2000). «2:Boole Turns Logic into Algebra».mEngines of Logic.
Mathematicians and the Origin of the Computer (em inglês) (New York: W. W.
Norton).
4