Ciencias_e_Matematica_do_Sol_e_do_Gnomon

Ciências e Matemática do Sol e do Gnômon
Resumo:
José Antonio Salvador, D. Sc. , DM – UFSCar
[email protected]
Lembrando Galileu que há 400 anos apontou a primeira luneta para o céu
inaugurando uma nova era na Astronomia, e os 40 anos em que o homem pisou
na lua pela primeira vez, revolucionando não só a ciência e tecnologia, como a
visão do homem diante do universo, achamos oportuno enfocar o aprendizado de
conceitos matemáticos baseados em simples observações como a projeção da
sombra solar de um gnômon (haste reta perpendicular a uma superfície plana, lisa
e horizontal), na realização de experiências de observação da direção, projeção e
tamanho da sombra para a determinação do meridiano local, construção da rosa
dos ventos, medida de alturas de objetos inacessíveis, medida da circunferência
da terra, construção de relógios de Sol, etc. O questionamento de tais problemas
pode motivar tanto o professor quanto os estudantes para o entendimento dos
movimentos da Terra e da importância do Sol e do seu caráter multidisciplinar
gerando o gosto dos estudantes pelas descobertas das ciências e matemática. O
ato de fazer experiências com tamanhos e direções de sombras, determinação do
meridiano local e dos pontos cardeais explorando medida, ângulo, distância,
bissetriz, perpendicularidade, circunferência, triângulo, semelhança, regra de três,
trigonometria, etc. contribuirá para o aprendizado do estudante e vem ao encontro
das competências e habilidades pregadas pelos Parâmetros Curriculares
Nacionais (PCNs) no que toca a representação e comnicação, investigação e
compreensão e contextualização socio-cultural.
Palavras Chaves: Ensino de ciências e matemática, orientação, medidas e
relógios de sol.
1. Introdução
Ao perguntarmos onde o sol nasce, a resposta comum é que o sol nasce
no leste. Mas quando é que isso acontece? Será que o sol nasce sempre no
mesmo local? O sol nasce todo dia a mesma hora onde você mora? O sol fica a
pino na sua região? O sol sempre fica a pino ao meio-dia? Em que dia(s) do ano o
sol fica a pino ao meio-dia? Em que lugar(es) da superfície terrestre é possível ver
o sol a pino ao meio-dia? A sombra de um objeto muda de direção e de tamanho
durante o dia? Durante os vários dias do ano a projeção da sombra mínima da
ponta de uma haste vertical varia de tamanho? Será que o sol nasce no mesmo
local no início das estações do ano? E o pôr-do-sol é sempre no mesmo local?
Como podemos nos orientar e nos localizarmos? Em que direção fica a frente da
sua casa? E da sua escola? Como orientar a construção de uma casa ou de uma
escola de modo que ela receba a máxima iluminação natural? Como inclinar o
telhado de uma construção para colocação de placas solares visando otimizar a
energia recebida nos meses de inverno? Questionamentos como esses e outros
relacionados podem despertar o interesse nos estudantes para as Ciências e
Matemática e fazer com que eles fixem os conteúdos naturalmente.
Desde criança percebemos o movimento aparente observando os mourões
de uma cerca fixos nas margens de uma estrada que vão ficando para trás
quando viajamos sentados no banco de um veículo. O movimento aparente deles
é no sentido contrário ao movimento do veículo. Da mesma forma como nossos
antepassados, observamos o movimento circular aparente de toda a esfera
celeste de leste para oeste todos os dias. Em particular, o sol nasce de um lado
no horizonte se elevando, iluminando e aquecendo a terra à medida que vai
alcançando um ponto mais alto no céu e depois se põe do outro lado completando
um arco de circunferência até desaparecer do outro lado. Chega a noite vem as
estrelas que começam a percorrer o céu aparentemente na mesma direção do
Sol. Hoje sabemos que a Terra tem um movimento diário de rotação ao redor de
seu próprio eixo de oeste para leste e de translação anual ao redor do Sol durante
cerca de 365,25 dias com uma velocidade aproximada de 30000 m/s, além de
outros movimentos.
A simples observação diária do nascimento do Sol, através de uma fresta
na porta ou janela de nossa casa, durante um intervalo de alguns dias ou
semanas nos mostra que ele não nasce no mesmo local todos os dias. E então,
onde fica o Leste (o oriente?).
2. Orientar é procurar o oriente
A necessidade de contagem do tempo e de orientação na superfície
terrestre ou no mar se intensificou com o surgimento das grandes navegações e
tornou-se indispensável para o homem.
Uma das primeiras referências para nos orientarmos é considerarmos, por
exemplo, os objetos fixos ao nosso redor e a observação dos astros no céu.
As primeiras civilizações observaram certas particularidades no céu, como
a posição da estrela Polar na cauda da constelação da Ursa Menor que está
praticamente fixa na direção do Pólo Norte Celeste, que é o prolongamento do
Pólo Norte terrestre. As estrelas circunvizinhas parecem descrever uma
circunferência completa ao seu redor. A sua projeção no horizonte indica a
direção Norte e orienta os povos daquele hemisfério.
Os povos do sul e os primeiros navegantes que se aventuraram para cá
consideravam a constelação do Cruzeiro do Sul como uma boa referência para
determinar o Pólo Sul.
De fato, tomando como referência o braço maior do Cruzeiro, formado por
2
Fig. 1. A orientação pelos astros: Estrela Polar e o Cruzeiro do Sul
um arco de 6º. unindo a estrela α, (Magalhães) a mais brilhante que se encontra
no pé do cruzeiro e representa o estado de São Paulo na Bandeira brasileira, e a
estrela γ  (Rubídea), na cabeça do cruzeiro, e prolongando aproximadamente
quatro vezes e meia, obtemos um ponto na esfera celeste, o Pólo Sul Celeste,
que projetado no horizonte nos dá a direção Sul.
Com a descoberta do ímã no II milênio a.C, também se construiu a
Bússola, um instrumento de orientação composto de uma agulha magnética na
horizontal suspensa pelo centro de gravidade apontando para a direção Norte-Sul
magnética. A bússola aponta para o Pólo Norte Magnético, que embora não
coincida exatamente com o Pólo Norte Geográfico, nos fornece uma orientação
aproximada para a maioria dos pontos da superfície terrestre.
A localização do Pólo Sul Celeste pelo Cruzeiro do Sul durante uma noite
estrelada pode ser imprecisa, entretanto é possível determinar a direção Norte–
Sul com mais precisão fazendo uma simples experiência da projeção da sombra
de um gnômon (haste fincada verticalmente no solo) durante um dia ensolarado.
Assim, outro método de orientação consiste na determinação da linha
meridiana local, a linha Norte–Sul do observador. A posição do sol pela manhã e
tarde é importante, não só pela luz, calor, energia e vida que ele nos fornece, mas
para nos orientarmos geograficamente. Observe que a trajetória aparente do sol
na esfera celeste durante um dia ensolarado é um arco de circunferência em
torno do eixo terrestre e faz com que a direção da sombra de um gnômon varie de
posição e de tamanho durante os dias. Nas várias épocas do ano, podemos
observar o tamanho mínimo da sombra de um gnômon ao longo de um dia.
Fig. 2. Sombra mínima de um gnômon nos solstícios de verão (SV),
equinócios (E) e solstícios de inverno (SI)
O segmento de reta da sombra mínima do gnômon (vertical) num dia
ensolarado está contido no meridiano local, e nos dá a direção Norte-Sul. A linha
3
perpendicular ao meridiano local nos dá a direção Leste-Oeste verdadeira. É fácil
observar que os tamanhos das sombras de um gnômon ao longo do dia vão
diminuindo da manhã até o meio-dia solar verdadeiro, quando o sol atinge o ponto
mais alto no céu cruzando o meridiano celeste local, e depois, vai aumentando à
medida que vai entardecendo.
A linha meridiana local também pode ser obtida marcando a direção da
bissetriz das sombras da manhã e da tarde de mesmo tamanho de um gnômon,
especialmente num dia de equinócio para quem vive entre os trópicos, em que a
sombra mínima é nula, pois o sol passa pelo zênite do observador exatamente ao
meio dia solar verdadeiro. O procedimento consiste em fincar um gnômon num
local C onde se tenha sol de manhã e de tarde, pelo menos próximo do meio dia
solar verdadeiro. Usa-se um fio de prumo para certificar-se de que a haste está
realmente na posição vertical e conseqüentemente apontando para o centro da
terra. Traça-se no chão vários arcos de circunferências de sombra concêntricos
das extremidades da sombra do gnômon, usando, por exemplo, um pedaço de
barbante amarrado no pé do gnômon C e marcam-se neles os raios de sombra da
manhã (s1 e s3), ligando os pontos extremos das sombras com o centro C, no pé
do gnômon conforme a Fig. 4.
Fig. 4. Arcos e raios de sombra de mesmo tamanho, bissetriz e linha meridiana
Durante à tarde marca-se também os raios de sombra (s4 e s2) projetados
pela haste que atingem a extremidade de cada um dos arcos de circunferências
feitos no período da manhã, de modo a obter vários ângulos com vértices no pé
da haste C, cujos lados são os pares de raios de um arco de uma mesma
circunferência de sombra. Traça-se a bissetriz de cada par desses raios de
sombra congruentes. Elas coincidem? Evidentemente que sim. É a bissetriz
comum destes ângulos de sombra de mesmo tamanho que é a linha meridiana do
local, indicando a direção Norte-Sul (N - S).
É importante em cada etapa do experimento a discussão dos conceitos de
perpendicularismo, ao fincar o gnômon no solo, bem como questionar como os
operários das construções prumam os muros e paredes, como fazem as
medições, cálculos e como eles orientam as construções de modo que otimizem a
energia solar recebida durante o dia. Explorando o perpendicularismo entre a
linha meridiana, obtemos a linha Leste-Oeste (L-O ou L-W) obtendo os pontos
cardeais a partir do meridiano local. Com as linhas N-S e L-O podemos construir a
Rosa dos Ventos.
Tomando-se a direção das bissetrizes dos pontos cardeais, N-S-L-O
4
Fig. 3. Rosa dos Ventos
obtém-se os 4 pontos colaterais localizados entre os pontos cardeais, Nordeste
(NE), Noroeste (NO), Sudeste (SE) e Sudoeste (SO ou SW). Do mesmo modo, as
bissetrizes dos pontos colaterais geram os 8 pontos subcolaterais, localizados
entre um ponto cardeal e um ponto colateral, Norte-nordeste (NNE), Nortenoroeste (NNO), Leste-nordeste (ENE), Leste-sudeste (ESSE), Sul-sudeste
(SSE), Sul-sudoeste (SSO). Oeste-sudoeste (OSO) e Oeste-noroeste (ONO) e
em seguida obtém-se os 16 pontos intermediários localizados entre dois pontos
(cardeal e colateral ou subcolateral), chamados de intermediário entre S e SSE;
intermediário entre NE e NNE, etc. Observe a progressão geométrica dos
números de direções à medida que vamos traçando tais bissetrizes.
Verifique num globo terrestre se Assuã, antiga Siena, e a cidade de
Alexandria usadas por Eratóstenes no século III a.C. para medir a circunferência
da Terra estão sobre um mesmo meridiano. Observe que uma linha N-S sobre um
globo é uma geodésica, uma circunferência máxima da Terra chamada meridiana.
Explore as coordenadas geográficas para entender os conceitos de latitude e
longitude. Imagine como devem ser as coordenadas celestes: ascensão reta e
declinação dos astros. Localize outras escolas ou locais que estão sobre o
mesmo meridiano e discuta os resultados das observações e experiências sobre
as posições do sol durante vários horários de um mesmo dia, a altura máxima do
Sol e consequente sombra mínima de um gnômon, etc. nos diversos locais sobre
um mesmo meridiano.
É fácil de ver que na maioria das cidades existem obeliscos para enfeitar
suas praças, jardins ou instituições, provavelmente herdados do simples gnômon,
usado para marcar as horas do dia, início das estações do ano, etc. localizado no
centro das aldeias ou vilas das primeiras civilizações. Muitas civilizações
construíram suas vilas, templos para cultos religiosos e adorações seguindo uma
orientação especial do movimento aparente dos astros. Evidências aparecem nos
sítios arqueológicos das várias partes do mundo: Stonehenge; Carnac;
Almendres; Pirâmides do Egito; os impérios dos povos Incas, Maias e Astecas,
etc.
5
3. Sombra e Medidas de Objetos Inacessíveis
Quando Tales de Mileto visitou o Egito no século VI a.C. conta-se que ele
calculou a altura da Grande Pirâmide, orientada precisamente para os pontos
cardeais, deixando-nos uma técnica para medir alturas de objetos inacessíveis.
Provavelmente desenhou no chão uma circunferência com raio igual ao tamanho
de um gnômon e no momento em que a sombra dele atingia a circunferência, a
sombra da pirâmide também ficava igual à altura dela, provavelmente com isso,
nascia uma das primeiras aplicações do triângulo (Fig. 5). Utilize as idéias de
Tales para medir a altura do prédio da escola ou um objeto inacessível. E quando
a sombra do gnômon não for igual ao tamanho dele, como podemos calcular a
altura da pirâmide utilizando semelhança de triângulos?
Fig. 5. Medida da altura da Pirâmide
Outra proeza realizada no século III a.C. foi quando Eratóstenes
considerou três hipóteses fundamentais para calcular a medida da circunferência
da Terra (cerca de 40000 km): que a Terra era esférica; que o sol era muito maior
do que a Terra e estava muito distante de modo que os raios solares chegassem
paralelos aqui; e que as cidades de Alexandria e Siena (atual Assuã) estavam
num mesmo meridiano terrestre, conforme esquema da Fig. 6.
Fig. 6. Esquema de Eratóstenes
Ele calculou o comprimento da circunferência da Terra, com a suposição
de que a diferença dos ângulos de sombras dos raios solares α quando
projetados simultaneamente nos dois locais sobre um mesmo meridiano está para
a distância d que os separa, assim como o ângulo da circunferência da Terra
360º. está para todo o comprimento C dela. Utilizou uma regra de três simples
6
(α /d = 360/C), as propriedades da circunferência e dos ângulos alternos internos
de duas retas paralelas (raios de Sol) cortadas por uma transversal.
Experimente reproduzir a experiência de Eratóstenes para determinar o
tamanho de uma esfera de isopor. Coloque dois estiletes (gnômons)
perpendiculares a superfície esférica, alinhe sobre o meridiano local. Se nenhum
deles ficar na direção dos raios solares ao meio dia solar verdadeiro, verifique que
a diferença dos ângulos de sombra dos estiletes está para a distância entre eles
assim como 360o. está para o comprimento da esfera.
4. Relógio Solar
O gnômon é um relógio de sol vertical, que foi muito usado pelas primeiras
civilizações.
Fig. 7. Gnômon e Tamanho de Sombra
A observação do tamanho e da direção da sombra do gnômon nas várias
épocas do ano, ainda é utilizada por tribos indígenas brasileiras para orientação
de suas aldeias e marcação do tempo (AFONSO [2006] e SCANDIUZZI [2000]),
mesmo nos dias de hoje com as novas tecnologias como o GPS ( ALVES [
2006]).
Conhecendo-se a linha meridiana e a latitude do local podemos construir
um dos mais simples relógios de sol, o de mostrador equatorial. A idéia é apontar
um gnômon para o pólo celeste elevado do local, como se fosse o eixo no qual o
mundo aparentemente gira 360º. em 24 horas. Supondo o movimento de rotação
da terra uniforme durante o dia, graduamos a extremidade de um disco
semicircular das 6 às 18 horas, de hora em hora com intervalos igualmente
espaçados de 15 graus, pois a cada rotação da terra de 15º. corresponde a 1
hora.
O disco circular centrado no eixo, como se e a concavidade da esfera
celeste fosse invertida num plano perpendicular ao gnômon (apontado para o pólo
elevado) pode ser fixado numa placa horizontal, inclinada de um ângulo de
90 − φ , em que φ é a latitude local (altura do pólo elevado) conforme Fig. 8. O
eixo da esfera celeste funciona como um grande ponteiro fixo para determinação
das horas.
7
Fig. 8. Relógio de Sol com montagem equatorial
Na construção descrita não levamos em conta os efeitos representados
matematicamente pela equação do tempo, que estabelece a diferença entre o
tempo solar verdadeiro e o tempo solar médio. Como o movimento aparente do
Sol ocorre ao longo da eclíptica, e não no equador celeste e com uma velocidade
variável, pois a órbita da Terra é elíptica (mas, nem tanto excêntrica como
geralmente aparece nas ilustrações) e não circular, propomos a construção de um
analema, um gráfico ou uma tabela indicando a diferença da hora do relógio solar
observada nas várias épocas do ano com a hora legal.
Outro tipo de relógio solar é o de mostrador horizontal. Composto de um
gnômon com ângulo de inclinação da latitude local φ , apontando para o pólo
celeste elevado projetando sombra das horas no plano do horizonte local (Fig. 9).
Fig. 9. Relógio de Sol com mostrador horizontal, Águas de São Pedro – SP
Os valores dos ângulos θ no plano do horizonte correspondentes a cada
hora do ângulo horário do Sol na montagem equatorial pode ser calculado
utilizando trigonometria.
Para determinar os ângulos horizontais das horas inteiras podemos utilizar
uma figura auxiliar constituída do tetraedro POQR conforme a Fig. 10, e comparar
as relações trigonométricas de suas faces constituídas dos triângulos retângulos
POQ, PQR e OQR. Na Fig. 10, observamos que o triângulo POQ é retângulo em
O, e verificamos as seguintes relações:
8
Fig. 10 Montagem Horizontal de um Relógio de Sol
sin( φ ) =
OQ
OP
OQ
cos ( φ ) =
e tan( φ ) =
PQ ,
PQ
OP
Da primeira e terceira relações acima, escrevemos;
OQ = PQ sin( φ ) , e OQ = OP tan( φ )
O triângulo PQR retângulo em Q nos dá a tangente da abertura θ ;
QR
tan( θ ) =
PQ
Do triângulo OQR, retângulo em Q escrevemos a tangente do ângulo w de
abertura circular superior da Fig. 10 como
QR
tan( w ) =
OQ
Multiplicando e dividindo a tan( θ ) pelo tamanho do segmento OQ ,
escrevemos a tangente do ângulo θ de abertura no plano horizontal com relação a
sombra do meio dia como,
QR
QR OQ
tan( θ ) =
=
PQ
OQ PQ
Usando a expressão para tan( w ) e sen( φ ) na expressão anterior obtemos
tan( θ ) = tan( w ) sin( φ )
E assim, o ângulo θ pode ser dado em função do ângulo das horas na
montagem equatorial w e da latitude φ
θ := arctan( tan( w ) sin( φ ) )
Para cada ângulo w = 15 n , das horas, temos para n = 0 correspondente a
w = 0, o ângulo de zero grau com a projeção da sombra sobre a linha meridiana
local, correspondente às 12 horas, ou ao meio dia verdadeiro local. Em dias
ensolarados, quando a sombra do gnômon estiver sobre cada uma das posições
graduadas das horas inteiras n = 6, 5, 4, 3, 2, 1, 0, −1, −2, −3, −4, −5, −6 , podemos
ver a seqüência de valores da hora solar verdadeira local desde 6 horas da
manhã às 6 horas da tarde
θn := arctan( tan( 15 n ) sin( φ ) )
9
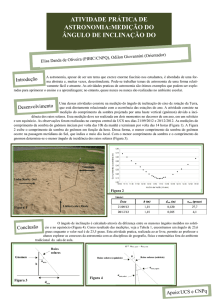
Para um ponto da superfície terrestre em frente ao Departamento de
Matemática da UFSCar com Latitude (Sul) 21 graus e 58 minutos (LatitudeDM =
21,96º.), o cálculo dos ângulos de sombra das horas no plano horizontal formados
com a direção do meridiano (meio dia) pode ser feito com uma calculadora ou
computador:
θ12 = 0 º, θ11 ≈ 5,7º, θ10 ≈ 12,2º, θ9 ≈ 20,5º, θ8 ≈ 32,9º, θ7 ≈ 54,4º, θ6 = 90º
e devido a simetria temos os mesmos ângulos para tarde:
θ13 ≈ 5,7º, θ14 ≈ 12,2º, θ15 ≈ 20,5º, θ16 ≈ 32,9º, θ17 ≈ 54,4º e θ1 8 = 90º.
Para w = 15 * 2 = 30 graus correspondente às 10 horas local, θ10 =
12,18686779, e devido a simetria, às 14 horas temos o mesmo ângulo de sombra
θ14 do outro lado do meridiano. Para as devidas correções podemos construir
também podemos propor a observação diária e construir um analema.
5. Algumas Sugestões de atividades
Alguns temas relacionados com a astronomia, que podem contribuir para o
aprendizado de vários conceitos matemáticos e de ciências:
1.
2.
3.
4.
5.
6.
7.
8.
9.
Explorar a curva obtida ao traçarmos a ponta da sombra de um gnômon
vertical durante um dia. Qual é o tamanho da sombra mínima durante
uma semana, um mês e ao longo do ano.
Determinar o meridiano local para fazer uma rosa dos ventos florida na
escola, praça ou jardim. Integre com atividades de outras ciências
plantando flores de cores ou tonalidades diferentes em cada direção. As
letras N, S, L e O podem ser marcadas enterrando pela metade garrafas
tipo pet contendo água clorada colorida e fixadas no solo. Respeite
sempre os três R´s: Redução, Reutilização e Reciclagem de materiais e
o uso de sucatas para várias atividades educacionais relacionadas.
Conhecendo os pontos cardeais propor brincadeiras de caça ao tesouro
com os estudantes das primeiras séries, enfocar o problema da direção
com desafios matemáticos.
Propor a construção um relógio de Sol (pode ser com uma garrafa pet
cilíndrica reta transparente).
Utilizar software Google Earth e a distância entre duas cidades para
calcular a medida da Terra.
Explorar um globo terrestre e compreender as coordenadas geográficas,
os meridianos e paralelos, os fusos horários nos estados do Brasil e no
mundo, o meridiano referencial de Greenwich e os fusos horários nas
várias partes do mundo. Discuta o horário de verão e suas vantagens e
desvantagens.
Pesquisar as coordenadas cartesianas planas, as coordenadas
esféricas e as coordenadas celestes.
Construir instrumentos de medida como: Astrolábio, Bússola, Sextante e
outros que foram usados nas grandes navegações antes mesmo da
descoberta do Brasil.
Pesquisar sobre os monumentos antigos como o de Stonehenge no sul
da Grã-Bretanha, que provavelmente serviu de observatório astronômico
e de orientação para aqueles povos há alguns milênios.
10
10.
11.
12.
13.
14.
15.
Pesquisar letras de músicas, poesias, romances, peças teatrais,
filosofia, etc. contendo tópicos abordando os astros (Sol, Lua, etc.).
Como os historiadores como Heródoto descreveu o mundo na sua
época ou como o poeta Dante descreveu o mundo nos séculos XIII e
XIV numa das famosas obras literárias medievais, a Divina Comédia.
Explorar a luz do sol e os fenômenos como a fotossíntese, a
decomposição da luz, o arco-iris (ou duplo arco-iris); a composição
química do sol; as reações nucleares que ocorrem no interior do sol ou
de uma estrela, etc.
Fazer uma experiência com uma lanterna e um globo terrestre (ou bola
de isopor) para compreender a iluminação dos hemisférios terrestre nas
várias épocas do ano. Pesquisar a iluminação e a ventilação natural da
sua casa, local de trabalho ou de estudo.
Elaborar uma ficha de atividades com questões a serem exploradas em
cada experimento, contendo dados como: Nome da Escola; Estudante
(ou grupo de estudantes); Professor(es); Localidade (Cidade, Estado,
País); Latitude local; Longitude local; Altitude, Data; Hora Local; Horário
do nascer do sol; Horário do pôr-do-sol; Tabela sobre o tamanho de uma
haste vertical, tamanhos da sombra e da direção dela nas várias horas
do dia, etc.
Utilizar o software stellarium para conhecer o céu do lugar onde você
mora e como veria o céu se morasse noutro hemisfério.
Pesquisar como Aristarco e outros filósofos antigos calcularam as
distâncias e os diâmetros do Sol e da Lua, etc. utilizando a
trigonometria.
Enfim, sugerimos a integração dessas atividades com outras disciplinas e com
outras escolas para o enriquecimento da abordagem.
Conclusão
Nesse trabalho discutimos uma maneira de despertar os estudantes para os
estudos de ciências e matemática levando em consideração o maior laboratório
natural que é o mundo que vivemos. Propomos observar com mais cuidado os
fenômenos diários como o movimento aparente do sol descrevendo arcos num
plano perpendicular ao eixo terrestre e suas consequências. Os tópicos
apresentados além de contemplar os PCNs podem ser abordados sempre que
possível e especialmente em 2009, em que comemoramos o Ano Internacional da
Astronomia.
7. Referências
AFONSO, G., Mitos e estações no céu tupi-guarani, Scientific American Brasil, 3847, No. 45, 2006.
11
ALVES, S., A matemática do GPS, RPM, 59, 2006.
BOCZKO, R., Conceitos de Astronomia, Edgard Blucher, 1998.
BOYER, C. B., História da Matemática, trad. Elza. F. Gomide, Ed. Edgard Blucher,
1974.
CIÊNCIA HOJE NA ESCOLA, Céu e Terra, SBPC, Rio de Janeiro, 1997.
FRIAÇA, A. C. S., DAL PINO, E., SODRÉ Jr., L., JATENCO-PEREIRA, V.,
Astronomia: uma Visão Geral do Universo, São Paulo: Edusp, 2000.
HOGBEN, L., Maravilhas da Matemática, trad. P. M. da Silva, Ed. Globo, Porto
Alegre, 1958.
MOURÃO, R. R., Manual do Astrônomo, Rio de Janeiro, Jorge Zahar Ed., 2004.
Oliveira Filho, K. e Saraiva, M. de Fátima, Astronomia e Astrofísica, 2a. Ed.,
Livraria da Física, São Paulo, 2004 e http://www.ufrgs.br/ufrgs/, 2009.
ROHR, RENÉ R. J., Sundials, History, Theory and practice, Dover, 1970.
SCANDIUZZI, P. P., Educação Indígena x Educação Escolar Indígena: Uma
Relação Etnocida em uma Pesquisa Etnomatemática, Tese de Doutorado,
UNESP, Marília, 2000.
SALVADOR, J. A., Matemática do Sol, Gnômon e Sombra, IX ENEM, BH, 2007.
DVD Série Exploração do Espaço e DVD Hubble: 15 anos de descobertas.
Scientific American Brasil. Duetto Editorial.
DVD Série Cosmos, Carl Sagan, Superinteressante. Editora Abril.
Coleção Civilizações Perdidas, Editora Abril.
http://www.cdcc.sc.usp.br
http://www.rio.rj.gov.br/planetario/
http://pcdsh01.on.br/ - Os Relógios e sua Evolução no Observatório Nacional.
http://www.astronomia2009.org.br/ (Ano Internacional da Astronomia)
http://www.bibalex.org/English/index.aspx, (Biblioteca de Alexandria)
http://www.google.com/sky (Simulação do Céu, Google Sky)
http://www.shatters.net/celestia/ (Celestia: Simulação do Céu)
http://www.stellarium.org (Stellarium: Simulação do Céu)
http://www.stargazing.net/astropc/pindex.html (Cartas Celestes)
12