Apostila de Matemática 13 – Circunferência

Apostila de Matemática 13 – Circunferência
1.0 Definições
Circunferência é o conjunto de todos os pontos equidistantes do centro.
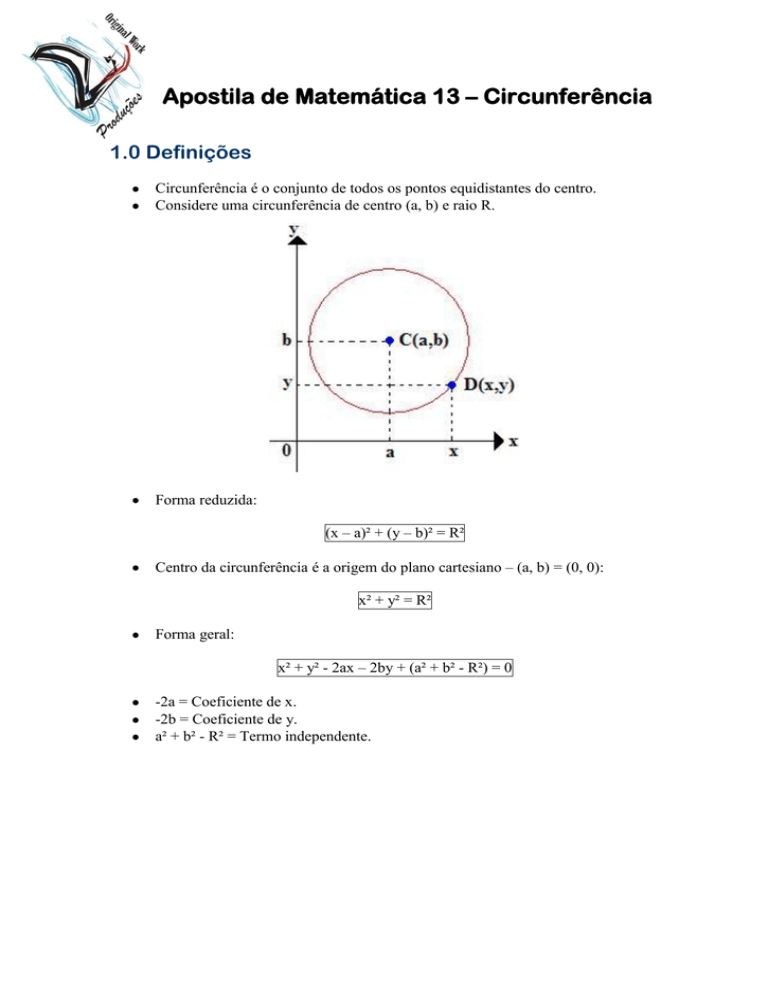
Considere uma circunferência de centro (a, b) e raio R.
Forma reduzida:
(x – a)² + (y – b)² = R²
Centro da circunferência é a origem do plano cartesiano – (a, b) = (0, 0):
x² + y² = R²
Forma geral:
x² + y² - 2ax – 2by + (a² + b² - R²) = 0
-2a = Coeficiente de x.
-2b = Coeficiente de y.
a² + b² - R² = Termo independente.
2.0 Posições Relativas
2.1 Ponto e Circunferência
Ponto pertence à circunferência – A distância entre o ponto e o centro é igual ao
raio.
Ponto é interno à circunferência – A distância entre o ponto e o centro é menor
que o raio.
Ponto é externo à circunferência – A distância entre o ponto e o centro é maior
que o raio.
2.2 Reta e Circunferência
A reta é secante à circunferência:
A reta toca 2 vezes pela circunferência.
A distância do centro da circunferência à reta é menor que o raio.
Δ>0
A reta é tangente à circunferência:
A reta toca 1 vez pela circunferência, perpendicularmente.
A distância do centro da circunferência à reta é igual ao raio.
Δ=0
A reta é exterior à circunferência:
A reta não passa pela circunferência.
A distância do centro da circunferência à reta é maior que o raio.
Δ<0
2.3 Duas Circunferências
Circunferências secantes – 2 pontos em comum.
Circunferências tangentes exteriormente – 1 ponto em comum.
Circunferências tangentes interiormente:
1 ponto em comum.
Os 2 centros e o ponto de tangência são colineares.
Circunferências externas – Nenhum ponto em comum.
1 circunferência interna a outra – Nenhum ponto em comum.