RESOLUÇÃO DA AVALIAÇÃO DE MATEMÁTICA – 3o ANO DO

RESOLUÇÃO DA AVALIAÇÃO DE MATEMÁTICA
– 3o ANO DO ENSINO MÉDIO –
DATA: 12/06/10
PROFESSORES: CARIBÉ E ROBERTO CIDREIRA
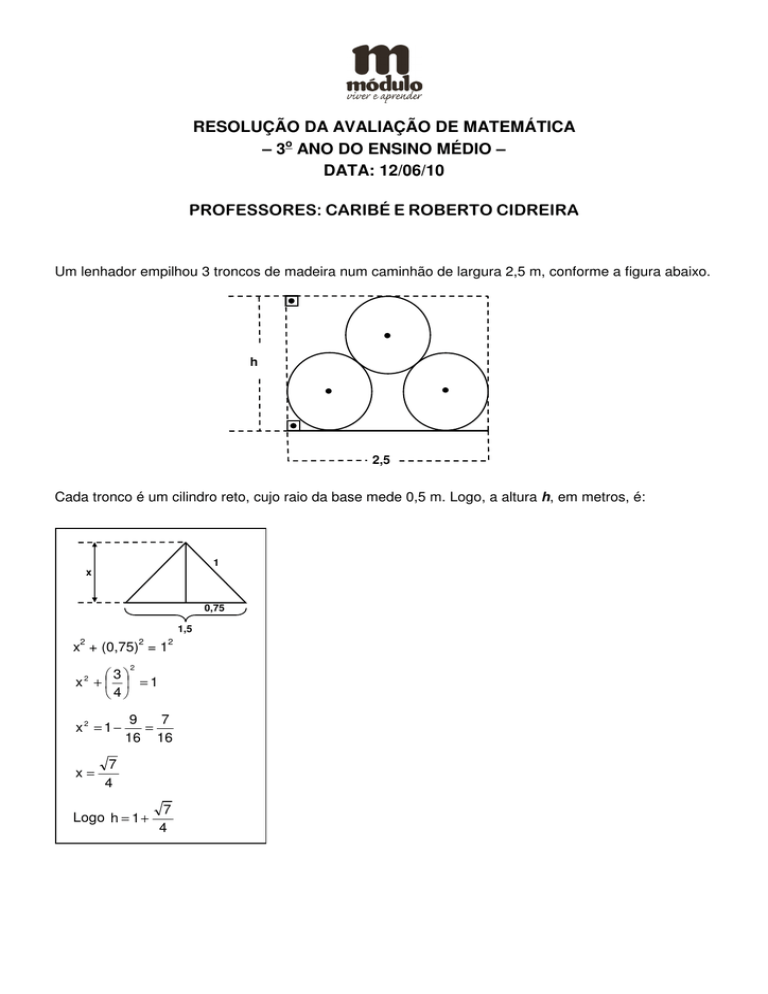
Um lenhador empilhou 3 troncos de madeira num caminhão de largura 2,5 m, conforme a figura abaixo.
h
2,5
Cada tronco é um cilindro reto, cujo raio da base mede 0,5 m. Logo, a altura h, em metros, é:
1
x
0,75
1,5
2
2
2
x + (0,75) = 1
2
3
x2 +   = 1
4
x2 = 1−
x=
9
7
=
16 16
7
4
Logo h = 1 +
7
4
Na figura a seguir, AB = 8 cm, BC = 10 cm, AD = 4 cm e o ponto O é o centro da circunferência.
O
D
A
B
C
O perímetro do triângulo AOC mede, em cm:
4 . (4 + 2R) = 8 . (8 + 10)
16 + 8R = 144
R
8R = 128
O
R
2
R = 16
4
A
8
B
10
C
Logo o perímetro do ∆AOC é igual a 20 + 16 + 18 = 54 cm.
D
Na figura abaixo, as medianas AE e BD são perpendiculares.
A
D
B
C
E
Sabendo que AC = 6 e BC = 8, calcule AB.
2
2
2
2
2
2
2
(I)
2
(II)
(2x) + y = 3 ⇒ 4x + y = 9
2
2
x + (2y) = 4 ⇒ x + 4y = 16
A
3
Somando I e II temos:
2
2
2
z
2
5x + 5y = 25 ⇒ x + y = 5
2
2
z = (2x) + (2y)
2
2
2
2
2
z = 4 . (x + y )
2
z =4.5
2
z = 20
z=2 5
D
y
2
2
z = 4x + 4y
2x
B
2y
x
4
E
3
4
C
Os ângulos internos de um triângulo ABC medem: Â = 30°, B̂ = 70º e Ĉ = 80º . Uma semicircunferência
de diâmetro AB intercepta os outros dois lados em P e Q.
A medida do arco PQ é igual a:
APQ = 140º
C
PQB = 60º
P
Q
APQ + PQB = 200º
AP + PQ + OB + PQ = 200º
30º
A
180º
70º
B
180º + PQ = 200º
PQ = 20º
Cinco livros diferentes, sendo três de Psicologia e dois de Anatomia, são colocados aleatoriamente
numa estante, um ao lado do outro.
A probabilidade de que os livros de mesmo assunto fiquem todos juntos, é:
Casos possíveis: P5 = 5! = 120
Casos favoráveis: P3 . P2 . P2 = 3!2!2! = 24
Probabilidade =
24 1
= = 20%
120 5
Em uma lanchonete, são servidas porções mistas de pastéis com 10 unidades, sendo 3 de carne, 3 de
queijo e 4 de camarão. Um cliente retira, aleatoriamente e sem reposição, 2 unidades de uma porção.
Com base nessas informações, pode-se afirmar que a probabilidade dos dois pastéis retirados serem
de camarão é igual a:
P=
4 3
2
. =
10 9 15
n
1

Sabe-se que, somando-se os coeficientes dos termos do desenvolvimento do binômio  2x 2 +  ,
x

obtêm-se 729.
O quarto termo desse desenvolvimento, segundo as potências decrescentes de x, é igual a:
n
(2 + 1) = 729
n
3 =3
6
n=6
Termo geral: Tp+1
 6
 1
=  (2x 2 ) 6 −p .  
x
p 
p
 6
3
 1
o
4 termo ⇒ p = 3 : T4 =  (2x 2 ) .  
x
3
= 20 . 8x 6 .
3
1
x3
3
= 160 x
8
1 

Qual o termo independente de x no desenvolvimento do binômio  x 3 −
 ?
2x 

Termo geral: Tp+1
8
8 −p
 − 1
=  (x 3 ) . 

 2x 
p 
p
para obtermos o termo independente devemos ter:
3 8-p
(x )
-p
0
.x =x
24 – 3p – p = 0
24 = 4p
p=6
Substituindo p = 6 no termo geral temos:
6
 8  3 2  − 1
 (x ) . 
 =
 2x 
 6
8.7 6
1
7
.x .
=
6
2 .1
64x
16
2
2
2
Sabendo que x; y e z são números reais e (2x + y – z) + (x – y) + (z – 3) = 0, então x + y + z é igual
a:
2x + 4 – z = 0
I
x–y=0∴x=y
II
z–3=0∴z=3
III
Substituindo II e III em I, tem-se:
2x + x – 3 = 0
3x = 3
x=1
Daí, vem:
y=1
Resp.: x + y + z = 1 + 1 + 3 = 5
*
Sendo a e b números inteiros positivos, e x ∈ N tal que x é menor que ab e x é maior que a(b – 1),
pode-se afirmar que o número de valores possíveis para x é:
I) Como:
a(b – 1) < x < ab
pode-se concluir que (b – 1) é antecessor de b.
II) Imagine que sendo a = 7 e b = 4 teremos (b – 1) = 3, daí vem:
a(b – 1) < x < ab
7 . (3) < x < 7(4)
21 < x < 28
Então existem 6 valores possíveis para x:
{22; 23; 24; 25; 26; 27}; o que equivale a dizer que existem (a – 1) valores possíveis de x.