Semelhança de triângulos - Imecc

Teorema da bissetriz de um triângulo
Teorema da bissetriz de um triângulo
MA092 – Geometria plana e analı́tica
Semelhança de triângulos - Potência de ponto
AM
BM
=
AC
BC
Francisco A. M. Gomes
UNICAMP - IMECC
Setembro de 2016
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
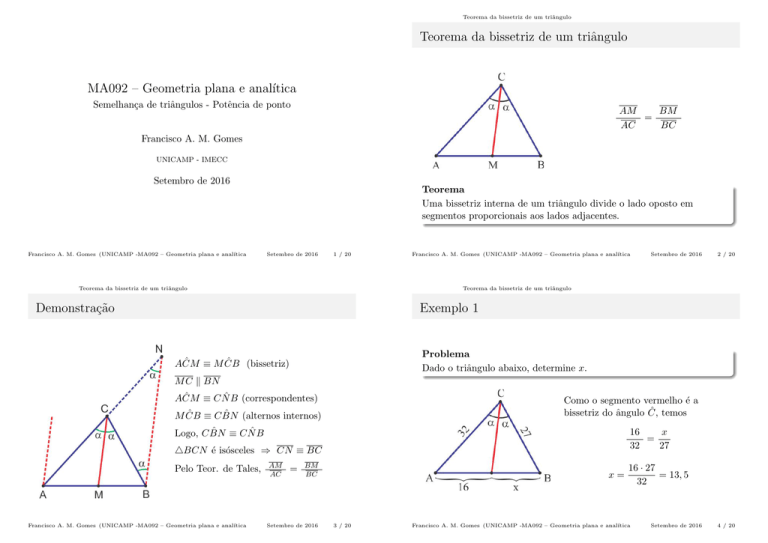
Teorema
Uma bissetriz interna de um triângulo divide o lado oposto em
segmentos proporcionais aos lados adjacentes.
Setembro de 2016
1 / 20
Teorema da bissetriz de um triângulo
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Setembro de 2016
2 / 20
Teorema da bissetriz de um triângulo
Demonstração
Exemplo 1
Problema
Dado o triângulo abaixo, determine x.
AĈM ≡ M ĈB (bissetriz)
M C k BN
AĈM ≡ C N̂ B (correspondentes)
Como o segmento vermelho é a
bissetriz do ângulo Ĉ, temos
M ĈB ≡ C B̂N (alternos internos)
16
x
=
32
27
Logo, C B̂N ≡ C N̂ B
4BCN é isósceles ⇒ CN ≡ BC
Pelo Teor. de Tales,
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
AM
AC
=
BM
BC
Setembro de 2016
x=
3 / 20
16 · 27
= 13, 5
32
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Setembro de 2016
4 / 20
Semelhança de triângulos
Semelhança de triângulos
Semelhança de triângulos
Exemplo 2
Problema
Sabendo que os triângulos ABC e DEF são semelhantes, determine x e
y.
 ≡ Â0
B̂ ≡ B̂ 0
Ĉ ≡ Ĉ 0
AB
AC
BC
= 0 0 =
0
0
AB
AC
B0C 0
Definição
Dois triângulos são semelhantes se e somente se têm os ângulos
correspondentes congruentes e os lados correspondentes proporcionais
8
x
=
5
2, 5
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Setembro de 2016
5 / 20
Semelhança de triângulos
⇒ x=4
8
6
=
5
y
⇒ y = 3, 75.
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Setembro de 2016
6 / 20
Semelhança de triângulos
Reta paralela ao lado de um triângulo
Critério de semelhança AA
 ≡ Â0
Ĉ ≡ Ĉ 0
4ABC ∼ 4DEC
⇓
4ABC ∼ 4A0 B 0 C 0
Teorema
Se uma reta é paralela a um lado de um triângulo e intercepta os
outros dois lados em pontos que não são vértices, então o triângulo que
ela determina é semelhante ao primeiro.
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Setembro de 2016
7 / 20
Definição
Se dois ângulos de um triângulo são congruentes a dois ângulos de
outro triângulo, então esses triângulos são semelhantes.
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Setembro de 2016
8 / 20
Semelhança de triângulos
Semelhança de triângulos
Critério de semelhança LAL
Critério de semelhança LLL
AC
BC
=
0
0
AC
B0C 0
Ĉ ≡ Ĉ
AB
BC
AC
=
= 0 0
A0 B 0
B0C 0
AC
0
⇓
⇓
4ABC ∼ 4A0 B 0 C 0
4ABC ∼ 4A0 B 0 C 0
Definição
Se dois lados de um triângulo são proporcionais aos lados
correspondentes de outro triângulo, e se os ângulos compreendidos
entre esses lados são iguais, então os triângulos são semelhantes.
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Definição
Se os três lados de um triângulo são proporcionais aos lados
correspondentes de outro triângulo, então os triângulos são
semelhantes.
Setembro de 2016
9 / 20
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Semelhança de triângulos
Setembro de 2016
10 / 20
Semelhança de triângulos
Exemplo 3
Resolução
Altura de uma caixa d’água
João quer calcular a altura de
uma caixa d’água.
Os raios de sol fazem ângulo α
tanto com João, como com a caixa
d’água.
Com a ajuda de Marcelo, ele
descobriu que, em certa hora do
dia, sua sombra mede 0,75 m,
enquanto a sombra da caixa
d’água mede 2,5 m.
Se João mede 1,8 m, qual é a
altura da caixa?
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Setembro de 2016
11 / 20
Desse modo, os triângulos ao lado
são semelhantes (critério AA).
x
2, 5
=
1, 80
0, 75
⇒
x=
2, 5 · 1, 8
4, 5
=
=6m
0, 75
0, 75
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Setembro de 2016
12 / 20
Potência de ponto
Potência de ponto
Segmentos secantes a uma circunferência
Demonstração
C P̂ A ≡ B P̂ A
C ÂP ≡ B D̂P
⇓
∆AP C ≡ ∆DP B
⇓
AP
CP
=
DP
BP
⇓
Teorema
AP · P B = CP · P D
Se dois segmentos AB e CD secantes à circunferência se cruzam em
um ponto P, então AP · P B = CP · P D.
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Setembro de 2016
13 / 20
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Exercicios
Setembro de 2016
14 / 20
Exercicios
Exercı́cio 2
Exercı́cio 1
Problema
Na figura abaixo, CM é a bissetriz relativa ao ângulo C Ĉ. Determine
o valor de x.
Problema
Sabendo que os triângulos ABC e DEC são semelhantes, mostre que
suas alturas mantêm a proporcionalidade dos lados, ou seja,
AB
CN
=
DE
CM
x = 15
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Setembro de 2016
15 / 20
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Setembro de 2016
16 / 20
Exercicios
Exercicios
Exercı́cio 3
Exercı́cio 4
triângulos semelhantes
Os lados do triângulo ABC medem 10 cm, 15 cm e 20 cm. Determine
os lados de um triângulo semelhante a ABC, com perı́metro igual a 36
cm.
8 cm, 12 cm e 16 cm
Largura de um rinque
Um rinque de patinação quadrado será construı́do em um terreno
triangular, como mostra a figura. Determine o comprimento máximo
do lado do rinque.
x = 14, 4 m
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Setembro de 2016
17 / 20
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Exercicios
Setembro de 2016
18 / 20
Exercicios
Exercı́cio 5
Exercı́cio 6
Problema
Determine o valor de x
Subindo a ladeira
Um homem, de 1,80 m de altura, sobe uma ladeira, conforme mostra a
figura. No ponto A está um poste vertical de 5 metros de altura, com
uma lâmpada no ponto B. Calcule o comprimento da sombra do
homem depois que ele subiu 4 m ladeira acima.
√
x=3 3
2,25 m
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Setembro de 2016
19 / 20
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Setembro de 2016
20 / 20