MA092 - Imecc

Equação da reta
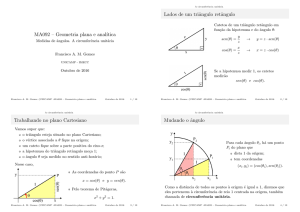
Coeficiente angular
Resultado
Uma reta não vertical, y = mx + q, tem coeficiente angular m dado
pela tangente do ângulo α medido no sentido anti-horário a partir da
horizontal:
m = tan(α)
MA092 – Geometria plana e analı́tica
Equação da reta. Retas paralelas e perpendiculares
Francisco A. M. Gomes
UNICAMP - IMECC
Novembro de 2016
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
m=
Novembro de 2016
1 / 20
yB − yA
= tan(α)
xB − xA
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Equação da reta
Novembro de 2016
2 / 20
Equação da reta
Equação da reta a partir de um ponto e um ângulo
Exemplo 1
Problema
Escreva a equação da reta que passa por (3, 2) e faz um ângulo de 30◦
com a horizontal.
Equação da reta
Se uma reta passa pelo ponto (x1 , y1 ) e possui um ângulo α com a
horizontal, então podemos representá-la por
y − y1 = m(x − x1 )
y − y1 = m(x − x1 )
√
◦
em que
m = tan(30 ) =
m = tan(α)
3
3
√
y−2=
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Novembro de 2016
3 / 20
3
(x − 3)
3
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Novembro de 2016
4 / 20
Equação da reta
Equação da reta
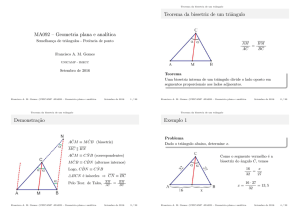
Equação da reta a partir de dois pontos
Exemplo 2
Equação da reta
Se uma reta passa pelos pontos
Problema
Escreva a equação da reta que passa por ( − 2, 1) e (3, 4)
(x1 , y1 )
e
(x2 , y2 )
m=
com x1 6= x2 , então podemos representá-la por
y − y1 = m(x − x1 )
em que
m=
[ ou y − y2 = m(x − x2 ) ]
y − y1 = m(x − x1 )
Novembro de 2016
5 / 20
3
y − 1 = (x − (−2))
5
⇒
3
y − 1 = (x + 2)
5
y2 − y1
x2 − x1
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
y2 − y1
4−1
3
=
=
x2 − x1
3 − (−2)
5
⇒
3
11
y = x+
5
5
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Equação da reta
Novembro de 2016
6 / 20
Retas paralelas
Exemplo 3
Retas paralelas
Problema
Encontre o ângulo que a reta que passa pelos pontos (−2, 1) e (3, 4) faz
com a horizontal.
Condição de paralelismo
Se as retas não verticais r e s são paralelas, então
mr = ms .
Além disso, se mr = ms , as retas r e s são paralelas.
m=
3
4−1
=
3 − (−2)
5
Como r e s são paralelas
αr = αs
α = arctan(3/5) ≈ 30, 96◦
Logo, tan(αr ) = tan(αs )
Assim, mr = ms
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Novembro de 2016
7 / 20
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Novembro de 2016
8 / 20
Retas paralelas
Retas paralelas
Exemplo 4
Exemplo 5
Problema
Determine se são paralelas as retas
r : y = 3x − 2
Problema
Encontre a reta s que passa por (5, 3) e é paralela a r : y = −2x + 1.
s : −15x + 5y + 4 = 0
e
Observamos que mr = 3.
Para achar ms , convertemos s à forma reduzida:
5y = 15x − 4
→
15x 4
−
y=
5
5
→
Obtendo o coeficiente angular:
ms = mr = −2
4
y = 3x −
5
Fazendo a reta passar por (5, 3)
Comparando os coeficientes angulares, notamos que
y − 3 = −2(x − 5)
ms = mr = 3
Logo, as retas são paralelas.
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Novembro de 2016
9 / 20
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Retas perpendiculares
Novembro de 2016
10 / 20
Retas perpendiculares
Retas perpendiculares
Demonstração
Se r e s são perpendiculares,
αs + 90◦ − αr = 180◦
Condição de perpendicularidade
Se as retas não verticais r e s são perpendiculares, então
ms = −
ou
1
.
mr
Logo,
Além disso, se ms = −1/mr , as retas r e s são perpendiculares.
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
αs = 90◦ + αr
Novembro de 2016
tan(αs ) = tan(90◦ + αr ) =
11 / 20
sen(90◦ + αr )
cos(90◦ + αr )
=
sen(90◦ )cos(αr ) + sen(αr )cos(90◦ )
cos(90◦ )cos(αr ) − sen(αr )sen(90◦ )
=
cos(αr )
1
=−
−sen(αr )
tan(αr )
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Novembro de 2016
12 / 20
Retas perpendiculares
Retas perpendiculares
Exemplo 6
Exemplo 7
Problema
Mostre que são perpendiculares as retas
r : y = 6x − 2
e
Problema
Encontre a reta s que passa por (−4, 7) e é perpendicular a
r : y = 5x − 2.
s : 2x + 12y − 15 = 0
Convertendo s à forma reduzida:
12y = −2x + 15
→
y=−
Obtendo o coeficiente angular:
2x 15
+
12 12
→
1
5
y =− x+
6
4
Observando que mr = 6 e comparando os coeficientes angulares:
1
1
ms = − = −
6
mr
ms = −
1
1
=−
mr
5
Fazendo a reta passar por (−4, 7)
1
y − 7 = − (x − (−4))
5
→
1
y − 7 = − (x + 4)
5
Logo, as retas são perpendiculares
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Novembro de 2016
13 / 20
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Exercı́cios
Novembro de 2016
14 / 20
Exercı́cios
Exercı́cio 2
Exercı́cio 1
Problema
Reescreva a equação da reta abaixo na forma reduzida e determine o
ângulo que ela faz com a horizontal.
Problema
Determine a equação da reta que passa pelo ponto (7, −5) e faz um
ângulo de 60◦ com a horizontal.
−x/3 − 4y − 5 = 0
y+5=
√
3(x − 7)
1
y = − 12
x−
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Novembro de 2016
15 / 20
5
4
α = −4, 76◦
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Novembro de 2016
16 / 20
Exercı́cios
Exercı́cios
Exercı́cio 3
Exercı́cio 4
Problema
As retas abaixo são paralelas?
Problema
Determine a equação da reta que passa pelo ponto (6, 4) e é paralela a
uma reta que passa por (−2, 5) e (4, 8).
2x − 3y + 7 = 0
e
5x − 4y + 1 = 0
y = 12 x + 1
Não
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Novembro de 2016
17 / 20
ou
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Exercı́cios
Novembro de 2016
18 / 20
Exercı́cios
Exercı́cio 6
Exercı́cio 5
Problema
Sejam dadas as retas
r : 3x + ay − 1 = 0,
y − 4 = 12 (x − 6)
Problema
Determine a equação da reta que é perpendicular a 3x − 2y + 4 = 0 e
passa pelo ponto (−2, 3).
e s : 2x − 4y + 4 = 0.
Determine o valor de a que faz com que r e s sejam perpendiculares.
a = 3/2
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Novembro de 2016
19 / 20
y − 3 = − 32 (x + 2)
Francisco A. M. Gomes (UNICAMP -MA092
IMECC)
– Geometria plana e analı́tica
Novembro de 2016
20 / 20