Lista de Exercícios - Radiciação

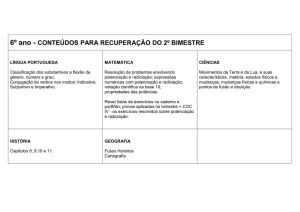
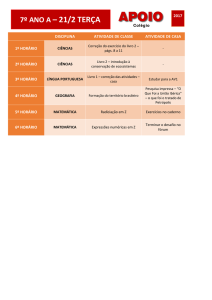
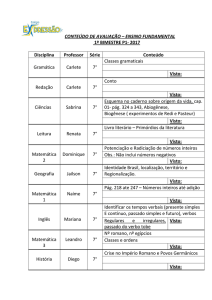
Lista de Exercícios - Radiciação
Nota: Os exercícios desta aula são referentes ao seguinte vídeo
Matemática Zero 2.0 - Aula 15 - Radiciação - (parte 1 de 2)
Endereço: https://www.youtube.com/watch?v=X6fw1EeQs2w
Gabaritos nas últimas páginas!
Atenção: alguns exercícios podem exigir conhecimentos de Potenciação
também. Não se esqueça que Potenciação e Radiciação são conceitos
muito ligados!
• Nota 1: Para todos os exercícios, considere U = ℝ
• Nota2: Pequenas variações na resposta são normais. Assim, para um
exercício cuja resposta final seja
,
as respostas 0,5 ou 2
são
corretas também. “Diferente” não significa necessariamente
“errado”. Na dúvida, pergunte.
• Nota 3: Alguns exercícios são particularmente difíceis e podem
exigir conhecimentos adicionais (fatoração, equações etc). Caso não
saiba, tente entender a resolução e/ou pergunte. Tais questões servem
para que você consiga aumentar o próprio nível desde já.
E1: Simplifique:
Página 1 de 17
Lista de Exercícios - Radiciação
E2: Simplifique (quando possível):
E3: Simplifique:
E4: Considere Verdadeiro ou Falso:
E5: Qual o maior número?
√27 ou √3 ? Justifique.
E6(Unicamp): Dados dois números positivos, √3 e √4, determine o
maior.
Página 2 de 17
Lista de Exercícios - Radiciação
E7: Simplifique:
E8: Simplifique: 20
E9: Simplifique: 3√7
0e
(para
21
8
2√5
4 √7
√64
√20
0,25 2
2
E10 (UEPB): Efetuando ! " !2
"
2
resultado:
a)
%
&
71
2
b)
c)
&
'
E12 (Colégio Naval):
Efetuando
a) 4
√
b) √3
E13 (Colégio Naval):
a) 1
b) 2
√
*√
c) √2
3
c) 3
√28
d) 1
E11: Simplifique a expressão: (
*√
0).
6
√45
# $
3
6
e)
√( ⋅ (
3 1
temos por
1
2
√(
obtém-se:
d)
2 2 √2 d) 4
Página 3 de 17
e) 1
3
2 2√2
d) 5
é igual a:
Lista de Exercícios - Radiciação
Complementos de aula – Radical Duplo.
√, ou + √, é um radical duplo. Em muitos
casos, tal expressão pode ser convertida para a forma √- . ou
A expressão
√- +
..Por exemplo: considere a expressão
/
√0. Ela é
equivalente à expressão 1 √2. Note como elas são (aparentemente)
muito diferentes! Justamente por não ser uma transformação “óbvia”, a
simplificação de radicais duplos é muito cobrada em vestibulares militares
(ITA, EN...).
Como simplificar radicais duplos (quando possível):
Página 4 de 17
Lista de Exercícios - Radiciação
Exemplo:
Simplifique 3
Lembrete:
96
3
3 4 √5 6
8⇒9 61
3
3
√8 6
3
√8 6 √2
3
3
√8 6
√8 :
4
2
√8 6 1
2
1
2
2
3
7*8
2
4
7 8
1
√1
√2
E14: Simplifique.
Página 5 de 17
e 9 6 √3
5
Lista de Exercícios - Radiciação
E15: Qual o valor da expressão:
a) 0,3
=
<>3?,
<
<
;
b) √3
…A %
2
c) 1
B
C239
448
7
d) 0
E16 (EPCAr Modificado): Simplifique: 1,111 …
I
E√3F HH
H
G
B
√J
e) 1
K2√
√ *
L
E17 (Desafio): Determine os números racionais x e y tais que:
10
6 √3 6
Página 6 de 17
Lista de Exercícios - Radiciação
Gabarito:
E1:
E2:
Página 7 de 17
Lista de Exercícios - Radiciação
E3:
Página 8 de 17
Lista de Exercícios - Radiciação
E4:
E5: Lembrando da propriedade:
√27 6
√3 6
⋅
3 6
⋅
3
⋅
√3' 6 √3' .
√b N 6
O
6
OQ
3
b NP
e que 27 = 3³, temos:
Observe que agora ambas as raízes possuem mesmo índice (55). Podemos
então comparar os radicandos:
Como 3
3' , então √27
√3
Página 9 de 17
Lista de Exercícios - Radiciação
√b N 6
O
E6: Lembrando da propriedade:
√3 6
3 6
⋅
3 6 √81
b NP
OQ
√4 6 √4 6 √4 6 √64
⋅
temos:
Observe que agora ambas as raízes possuem mesmo índice (12). Podemos
então comparar os radicandos:
Como 81
R S
R S
E7:
64, então √3
6
2 x y 6 2
E8:
20
√20
20
21
5= 5
21
R S
R S
8
√16 6
2y
√4
6
√64 6
20
√21
2'
20
46
⋅x
21
20
⋅y
√8
6
86
√25 =
E9: Nota: você pode fatorar os números 20, 28 e 45 (de forma idêntica ao
que fizemos no E3). Outra alternativa, mais rápida – se você tiver prática –
é tentar “quebrar” os números em produtos, de forma que a simplificação
seja mais imediata. Se for complexo demais para você, use a fatoração
utilizada no E3.
3√7 2√5 4√7 √20 √28 √45 6
3√7 2√5 4√7 √5 ⋅ 4 √7 ⋅ 4 √9 ⋅ 5 =
3√7 2√5 4√7 2√5 2√7 3√5 =
(Reordenando)
3√7
5√7
4√7
3√5 2√7
2√5
2√5
3√5
Página 10 de 17
Lista de Exercícios - Radiciação
E10: ALTERNATIVA A
0,25 2
2
! " !2
"
2
!
√
2
2"⋅2
√
√
⋅K L
⋅K L
⋅
√
√
0,5
6E
K
K
[
&
=
&√ ⋅&V
&√ V
E√
F
WX
L
6a
L
L
√ *
Z
%
&
=
=
=
L
√ *
√ *
=
=
=
temos:
√ *
5A>3
K6E √ * F L
=
√ * F>√ * A =
√
3 1
3 1
&√ ⋅&V
Lembrando que >3
6
1
K
Lembrando que
K6
# $
3
6
6
#
$
3
6
?,'
6
6
5A 6 3
6E
√ F> *√ A
5 , temos:
=
Página 11 de 17
√ *
&
=
=
Lista de Exercícios - Radiciação
E11: Lembrando que >3
(
√2(
√( ⋅ (
√( 6
5A>3
E(
5A 6 3
√(F ⋅ >(
( 6 √2\ 6 √] ⋅ ( 6 2√(
5 , temos:
√(A 6
E12: Alternativa A
Página 12 de 17
K(2
(2 L 6
Lista de Exercícios - Radiciação
E13: Alternativa B
Página 13 de 17
Lista de Exercícios - Radiciação
E14: Lembrete:
3 4 √5 6
7*8
4
Página 14 de 17
7 8
e 9 6 √3
5
Lista de Exercícios - Radiciação
E14 (continuação):
Página 15 de 17
Lista de Exercícios - Radiciação
E15: ALTERNATIVA C
^>3?,
`K3 L
b3
d3
B
%
…A %
2
2
J
2
2
f1g √J 6 1
B
E16:1,111 …
1
1
10
9
10
9
0,111 …
1
9
2E√
√2&
239
√243e
d 2
239
√239
B
√J
26
8
9
2
= d 2
K2√
6
10
9
1A
6
2
%
√64
3 c
B
B
J
J √
3 e
√ *
L
[
E √3F _
%
B
E √3F a
√J
=
√3' e
√2 1
K2√2 1 L
2E√2 1F⋅>√2
F
239
B
B
√J
B
√J
B
√J
=
=
=
=f 2
=
6
6
Página 16 de 17
3g √J =
B
Lista de Exercícios - Radiciação
E17:
10
6 √3 6
Elevando-se ao cubo dos dois lados, temos:
10
6√3 6 E
10
6√3 6
Lembrando que >3
10
6√3 6
Note que
10
6√3 6
6
F ⇔
3
3
3
5A 6 3
33 5
3
⋅
6
335
⇔
3
5 , temos:
⇔
3
⇔
Agrupando (no segundo membro) os termos semelhantes, temos:
10
6√3 6 >
Colocando
10
6√3 6 >
3
A
>3
3
A
>3
em evidência:
A
A ⇔
⇔
Por comparação entre os dois membros, podemos concluir que:
i3
3
6 10>jA
6 6>jjA ⇔
6 3>jjjA
Substituindo o valor de y (y = 3) na equação II, temos:
3
3 6 6 ⇔ (Por Bhaskara, as raízes são 1 e -1).
No entanto, ao substituirmos y =3 (único valor de y) e 6 1 na primeira
equação, vemos que ela não é satisfeita. Logo, x = 1 e y = 3.
Portanto,
10
6 √3 6 1
√3
Página 17 de 17