bca CURSO ANUAL DE FÍSICA AULA 1 – Prof. Renato

CURSO ANUAL DE FÍSICA
AULA 1 – Prof. Renato Brito
BREVE REVISÃO DE GEOMETRIA PARA AJUDAR NO ESTUDO DOS VETORES
É importante que o aluno esteja bem familiarizado com as propriedades usuais da geometria plana, tais como Lei dos
senos, Lei dos cossenos, Teorema de Pitágoras, Propriedades dos triângulos retângulos, a fim de operar com os vetores
sem maiores dificuldades. Vamos a uma pequena revisão:
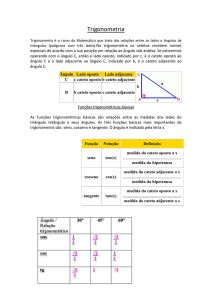
Geometria no triângulo retângulo:
Hipotenusa: lado oposto ao ângulo de 90º num triângulo retângulo. Somente triângulos retângulos tem hipotenusas.
Catetos: lados opostos aos ângulos agudos no triângulo retângulo.
hi p
n
o te
us
a
a
a
b
cateto
oposto ao
ângulo a
c
cateto adjacente ao ângulo a
Relações matemáticas que você deve saber
Pitágoras: a² = b² + c²
(válido só para triângulos retângulos)
sena 
tga 
cateto oposto b

hipotenusa
a
cos a 
b
cateto oposto

cateto adjacente c
cateto adjacente c

hipotenusa
a
(sena)2  (cos a)2  1
Todo estudante deve saber memorizado o seno, o cosseno e a tangente dos ângulos mais comuns que
aparecem na tabela abaixo. Normalmente o aluno acaba memorizando com o uso e a prática, fazendo
exercícios:
x
sen x
1
2
cos x
tg x
3
2
3
3
45°
2
2
60°
3
2
2
2
1
2
30°
1
3
CURSO DE MATEMÁTICA ANUAL – AULA 1 – Prof. Renato Brito
Breve revisão de Geometria para ajudar no estudo dos vetores 2
Geometria no triângulo qualquer
Lei dos Cossenos: calcula o 3º lado de um triângulo, do qual se conhecem dois lados e um ângulo.
a
c
esse é o lado
oposto a esse ângulo
a2 = b2 + c2  2.b.c. cosa
a
b
Note que, na lei dos cossenos, o lado a que aparece no 1º membro da fórmula é sempre o lado oposto ao ângulo a.
Para exemplificar o uso da Lei dos cossenos, determinaremos, a seguir, o comprimento do 3º lado de um triângulo do
qual conhecemos dois lados e um ângulo.
?
5 cm
60o
8 cm
esse é o lado
oposto a esse ângulo
a2 = b2 + c2  2.b.c. cosa
Chamaremos de a o ângulo de 60o do triângulo. O lado oposto ao ângulo a é sempre o lado a na lei dos cossenos e,
nesse exercício, será nessa incógnita. Os lados b e c podem ser escolhidos em qualquer ordem. Assim, temos:
a=?
a2 = b2 + c2  2.b.c. cosa
b = 8 cm
a2 = (8)2 + (5)2  2 x 8 x 5. cos(60o)
c = 5 cm
a2 = 64 + 25  40
2
a = 600
a = 49
a=7
Assim, o lado a desconhecido tem um comprimento de 7 cm.
CURSO DE MATEMÁTICA ANUAL – AULA 1 – Prof. Renato Brito
Exemplos resolvidos em vídeo
Questão 1
Um observador, estando a x metros da base de uma torre, vê o
topo sob um ângulo de 60º. Afastando-se 100 m em linha reta,
passa a vê-lo sob um ângulo de 30º. A altura da torre
corresponde, em metros, a:
a) 40.
b) 40 3.
c) 50 2.
d) 50 3.
e) 50.
Questão 2
Abílio (A) e Gioconda (G) estão sobre uma superfície plana de
uma mesma praia e, em um dado instante, veem, sob
respectivos ângulos de 30º e 45º, um pássaro (P) voando,
conforme é representado a seguir.
Considerando desprezível as medidas das alturas de Abílio e
Gioconda e sabendo que, naquele instante, a distância entre A
e G era de 240m, a quantos metros de altura o pássaro distava
da superfície da praia?
a) 60


c) 180 
d) 120 
e) 180 
b) 120

3 +1 m

3 + 1 m
3  1 m
3  1 m
3 +1 m
Questão 3
Dois pontos A e B, estão situados na margem de um rio e
distantes 40 m um do outro. Um ponto C, na outra margem do
ˆ mede 75º e o
rio, está situado de tal modo que o ângulo CAB
ˆ
ângulo ACB
mede 75º. A largura do rio, em metros,
corresponde a:
a) 15.
b) 20.
c) 25.
d) 30.
e) 35.
Breve revisão de Geometria para ajudar no estudo dos vetores 3
CURSO DE MATEMÁTICA ANUAL – AULA 1 – Prof. Renato Brito
Questão 4
A extremidade A de uma planta aquática encontra-se 10 cm
acima da superfície da água de um lago (figura 1). Quando a
brisa a faz balançar, essa extremidade toca a superfície da
água no ponto B, situado a 10 3 cm do local em que sua
projeção ortogonal C, sobre a água, encontrava-se inicialmente
(figura 2). Considere OA, OB e BC segmentos de retas e o
arco AB uma trajetória do movimento planta.
Pode-se afirmar que a profundidade do lago no ponto O em que
se encontra a raiz da planta, em centímetros, é:
a) 9.
b) 9 2.
c) 10.
d) 10 2.
e) 11.
Questão 5
A figura abaixo mostra que duas circunferências que se
tangenciam interiormente. A circunferência maior tem centro em
O. A menor tem raio r = 5 cm e é tangente a OA e OB.
Sabendo-se que o ângulo AOB mede 60º, a medida do raio da
circunferência maior corresponde a:
a) 10 cm.
b) 13 cm.
c) 15 cm.
d) 18 cm.
e) 20 cm.
Questão 6
Breve revisão de Geometria para ajudar no estudo dos vetores 4
CURSO DE MATEMÁTICA ANUAL – AULA 1 – Prof. Renato Brito
Breve revisão de Geometria para ajudar no estudo dos vetores 5
Dois irmãos herdaram um terreno em forma de um
paralelogramo ABCD, conforme ilustrado. Como pretendem
dividi-lo ao meio, resolveram passar uma cerca AC de
comprimento y. O valor de y, em metros, corresponde a:
10
.
a)
3
b) 10 2.
c) 5 3 .
d) 5 2.
5
.
e)
3
Questão 7
Observando o ângulo a no triângulo isósceles abaixo, determine o valor de sena sabendo que é válida a relação 4sena =
3cosa :
a) 0,1
b) 0,2
c) 0,4.
d) 0,5.
e) 0,6.
a
20
20
CURSO DE MATEMÁTICA ANUAL – AULA 1 – Prof. Renato Brito
EXERCÍCIOS PROPOSTOS
1) Leia o enunciado da questão e tente resolver.
2) Caso não consiga resolve, não tem problema, veja a
resolução da questão no final dessa apostila.
3) Em todas as questões abaixo, o aluno deve consultar os
valores dos senos, cossenos e tangentes de 30º, 45º e
60º que aparecem na tabela da nossa primeira página do
resumo teórico.
Questão 01
(UFPI) Um avião decola, percorrendo uma trajetória
retilínea, formando com o solo, um ângulo de 30º (suponha
que a região sobrevoada pelo avião seja plana). Depois de
percorrer 1 000 metros, qual a altura atingida pelo avião?
Questão 02
(Cefet – PR) A rua Tenório Quadros e a avenida Teófilo
Silva, ambas retilíneas, cruzam-se conforme um ângulo de
30º. O posto de gasolina Estrela do Sul encontra-se na
avenida Teófilo Silva a 4 000 m do citado cruzamento.
Portanto, determine em quilômetros, a distância entre o
posto de gasolina Estrela do Sul e a rua Tenório Quadros?
B
n
Te
o
ó ri
qu
a
s
d ro
30o
posto
Teófilo Silva
C
Questão 03
Determine o valor do lado oposto ao ângulo de 60º. Observe
figura a seguir:
Questão 04
Um pescador quer atravessar um rio, usando um barco e
partindo do ponto C. A correnteza faz com que ele atraque
no ponto B da outra margem, 240 m abaixo do ponto A. Se
ele percorreu 300 m, qual a largura do rio?
Breve revisão de Geometria para ajudar no estudo dos vetores 6
CURSO DE MATEMÁTICA ANUAL – AULA 1 – Prof. Renato Brito
Breve revisão de Geometria para ajudar no estudo dos vetores 7
Questão 05
Ao empinar uma pipa, João percebeu que estava a uma
distância de 6 m do poste onde a pipa engalhou. Renata
notou que ângulo a formado entre a linha da pipa e a rua
era 60°, como mostra a figura. Calcule a altura do poste.
Questão 6
Uma pessoa encontra-se num ponto A, localizado na base de um
prédio, conforme mostra a figura abaixo:
Se ela caminhar 120 metros em linha reta, chegará a um ponto B,
de onde poderá ver o topo C do prédio, sob um ângulo de 60°.
Quantos metros ela deverá se afastar do ponto A, andando em
linha reta no sentido de A para B, para que possa enxergar o topo
do prédio sob um ângulo de 30°?
Questão 7
Um avião está a 600 m de altura quando se vê a cabeceira
da pista sob um ângulo de declive de 30°. A que distância o
avião está da cabeceira da pista?
Questão 8
Determine os valores de x, y, w e z em cada caso:
CURSO DE MATEMÁTICA ANUAL – AULA 1 – Prof. Renato Brito
Breve revisão de Geometria para ajudar no estudo dos vetores 8
Questão 9
Em um triângulo retângulo, determine as medidas dos
ângulos agudos e da hipotenusa, sabendo que um dos
catetos mede 3 cm e o outro mede √3 cm.
Questão 10
(Cesgranrio) Uma rampa plana, de 36 m de comprimento, faz
ângulo de 30° com o plano horizontal. Uma pessoa que sobe a
rampa inteira eleva-se verticalmente de:
a) 6√3 m.
b) 12 m.
c) 13,6 m.
d) 9√3 m.
e) 18 m.
Questão 11
(UFAM) Se um cateto e a hipotenusa de um triângulo
retângulo medem 2a e 4a, respectivamente, então a
tangente do ângulo oposto ao menor lado é:
a) 2 3
b)
c)
d)
e)
3
3
3
6
20
20
3 3
CURSO DE MATEMÁTICA ANUAL – AULA 1 – Prof. Renato Brito
Breve revisão de Geometria para ajudar no estudo dos vetores 9
GABARITOS e RESOLUCOES
Questão 1
x
1000
sen30 
1
x

2 1000
2x  1000
x  500m
A altura será de 500 metros.
Questão 2
B
n
Te
A
o
ó ri
qu
a
s
d ro
x
30o 4000 m
posto
Teófilo Silva
C
Questão 3
Aplicaçao da lei dos cossenos
x² = 6² + 8² – 2 * 6 * 8 * cos 60º
x² = 36 + 64 – 96 * ½
x² = 100 – 48
x² = 52
√x² = √52
x = 2√13
Questão 4
3002 = x2 + 2402
90000 = x2 + 57600
90000 – 57600 = x2
x2 = 32400
x = 32400
x  180m
sen30 
BC
AC

1
x

2 4000
 x  2000 m  2 km
CURSO DE MATEMÁTICA ANUAL – AULA 1 – Prof. Renato Brito
Questão 5
C.O
tg a 
C.A
h
tg60 
6
h
3
6
h  6 3m
Questão 6
tg60 
3
h
120
tg30 
h
x
3 120 3

3
x
h
120
h  120 3 m
3 x  360 3
x  360m
Questão 7
600
sen30 
x
1 600

2
x
x  1200m
Questão 8
a) Através do cosseno de 30°, temos:
cos30 
cat. adjacente a 30
hipotenusa
3 16

2
x
3  x  16  2
x
32
3
Portanto, a hipotenusa mede
32
3
unidades.
Breve revisão de Geometria para ajudar no estudo dos vetores 10
CURSO DE MATEMÁTICA ANUAL – AULA 1 – Prof. Renato Brito
b) Através do seno de y:
cat.oposto a y
sen y 
hipotenusa
13
sen y 
26
1
sen y 
2
O seno de y é ½. Podemos então concluir que
c) Pelo seno de 60°:
cat.oposto a 60
sen60 
hipotenusa
y = 30°.
3
w

2
18

Breve revisão de Geometria para ajudar no estudo dos vetores 11

w 9 3
Concluímos que w  9 3 unidades.
d) Através do cosseno de 45°:
cat.adjacente a 45
cos 45 

hipotenusa
z
40
2

2
2

x
2 20

2
z
40 2
2


2  z  20  2
x  20 2
Portanto, a hipotenusa mede 20 2 unidades.
Questão 9
Como sabemos apenas as medidas dos catetos, vamos utilizar o Teorema de Pitágoras para determinar a medida da
hipotenusa (h):
(hipotenusa)² = (cateto)² + (cateto)²
h² = 3² + ( 3 )²
h² = 9 + 3
h = 12
h = 2 3 cm
Considere um ângulo α oposto ao lado de 3 cm. Calculando sua tangente, temos:
cat. oposto a a
cat. adjacente a a
3 3
3
3
 tg a 
 3

tg a 

3
3
3
3
Se tg a  3 , logo α = 60°. Sabendo que a soma dos ângulos internos de um triângulo qualquer é 180° e que esse é um
triângulo retângulo, podemos determinar a medida de outro ângulo agudo β:
β + α + 90° = 180°

β + 60° + 90° = 180°

β + 150° = 180° 
β = 180° – 150° = 30°
tg a 

tg a 
3
Portanto, os ângulos agudos desse triângulo valem 30° e 60°.
Questão 10
Podemos representar no triângulo ilustrado a seguir a situação descrita no problema. A hipotenusa representa a rampa
percorrida pela pessoa citada:
Representação geométrica da questão 3
Na figura, a altura que a pessoa foi elevada está representada pelo lado vermelho (cateto oposto ao ângulo de 30°).
Vamos chamar esse lado do triângulo de x para determinar seu valor. Para tanto, utilizaremos a fórmula do seno:
sen30 
cat.oposto
hipotenusa

1
x

2 36

2x  36 
x  18m
Portanto, ao subir a rampa, a pessoa eleva-se verticalmente 18 m. Logo, a alternativa correta é a letra e.
CURSO DE MATEMÁTICA ANUAL – AULA 1 – Prof. Renato Brito
Breve revisão de Geometria para ajudar no estudo dos vetores 12
Questão 11
Pelo enunciado do exercício, sabemos que a hipotenusa mede 4a e um dos catetos mede 2a, mas não sabemos de qual
cateto se trata. Precisamos determinar a medida do segundo cateto. Chamando-o de c, pelo Teorema de Pitágoras,
temos:
(hipotenusa)² = (cateto)² + (cateto)²
(4a)² = (2a)² + c²
16a² = 4a² + c²
c² = 16a² – 4a²
c² = 12a²
c = 12 a2
c = 2a 3
Agora que conhecemos o terceiro lado da figura, podemos esboçar o triângulo com o qual estamos trabalhando:
Representação geométrica da questão 4
Vamos chamar de α o ângulo oposto a 2a, que é o menor cateto. Agora podemos determinar a tangente de α:
cat.oposto a a
2a
1
3
3
 tg a 



cat.adjacente a a
3
2a 3
3 3
Portanto, a alternativa que indica a resposta correta é a letra b.
tg a 