Matemática 1

Matemática 1
17. Admita que a valorização anual do preço de certo objeto é constante. Cinco
anos atrás, o objeto custava R$ 1.170,00, e o preço atual (em 2003) do objeto é
de R$ 1.230,00. Determine qual será o preço, em reais, do objeto em 2006 e
assinale a soma de seus dígitos.
Resposta: 15
Solução:
Em cinco anos, o preço do objeto se valorizou em 1230-1170=60 reais;
portanto, a valorização anual foi de 60/5=12 reais. O preço do objeto em 2006
será 1230+3.12=1266 reais.
18. Diluindo, em água, três copos de concentrado de laranja, podemos fazer sete
copos de suco. Para produzirmos treze copos de refresco, diluímos cinco
copos de concentrado em água. Quantos ml de água devemos adicionar a
700ml de suco para obtermos refresco?
Resposta: 80
Solução:
Em 700ml de suco temos 300ml de concentrado e 400ml de água. Com
300ml de concentrado, podemos fazer 300.13/5 = 780ml de refresco.
Portanto, devemos adicionar 80ml de água.
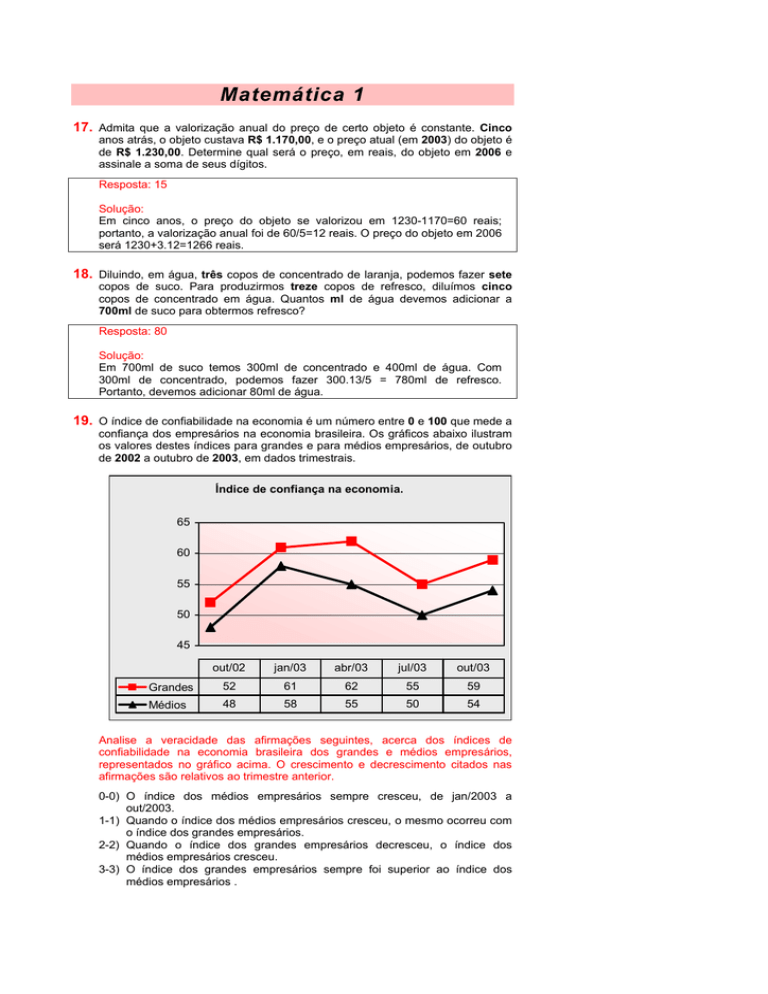
19. O índice de confiabilidade na economia é um número entre 0 e 100 que mede a
confiança dos empresários na economia brasileira. Os gráficos abaixo ilustram
os valores destes índices para grandes e para médios empresários, de outubro
de 2002 a outubro de 2003, em dados trimestrais.
Índice de confiança na economia.
65
60
55
50
45
out/02
jan/03
abr/03
jul/03
out/03
Grandes
52
61
62
55
59
Médios
48
58
55
50
54
Analise a veracidade das afirmações seguintes, acerca dos índices de
confiabilidade na economia brasileira dos grandes e médios empresários,
representados no gráfico acima. O crescimento e decrescimento citados nas
afirmações são relativos ao trimestre anterior.
0-0) O índice dos médios empresários sempre cresceu, de jan/2003 a
out/2003.
1-1) Quando o índice dos médios empresários cresceu, o mesmo ocorreu com
o índice dos grandes empresários.
2-2) Quando o índice dos grandes empresários decresceu, o índice dos
médios empresários cresceu.
3-3) O índice dos grandes empresários sempre foi superior ao índice dos
médios empresários .
4-4) Em outubro, o crescimento percentual do índice dos grandes empresários
foi igual ao dos médios empresários.
Resposta: FVFVF
Solução:
As justificativas de 0-0, 1-1, 2-2 e 3-3 são imediatas dos gráficos. Quanto a 44, temos que o crescimento percentual do índice dos médios empresários foi
de 100.4/50% = 8%, enquanto o dos grandes foi de 100.4/55 ≅ 7,3%.
20. Uma peça de mármore na forma de um paralelepípedo reto com comprimento
de 3m, largura de 40cm e espessura de 2,5cm pesa 75kg. Quantos quilos
pesa uma peça do mesmo mármore, com a forma de um paralelepípedo reto, e
2m de comprimento, 50cm de largura e 1cm de espessura?
Resposta: 25
Solução:
A primeira peça tem volume 3.0,4.0,025 = 0,03m3, e cada m3 do mármore
3
pesa 75/0,03 = 2500 kg. A segunda peça tem volume 2.0,5.0,01 = 0,01m , e
pesa 2500.0,01 = 25kg.
21. Uma loja oferece duas opções de pagamento:
Primeira opção: à vista, com desconto de 15% no valor da compra;
Segunda opção: em duas parcelas iguais, a primeira paga no momento da
compra e a segunda, passados dois meses da data da compra.
Indique o inteiro mais próximo do valor percentual da taxa de juros mensais
simples embutidos na segunda opção.
Resposta: 21
Solução:
Seja P o preço de venda do produto: à vista, o valor pago será 0,85.P; a
prazo, paga-se de juros 0,5.P-0,35.P=0,15.P; portanto, a taxa mensal de juros
é de 100.0,15.P/(2.0,35.P) ≅ 21,4%.
22. Um feirante comprou maçãs por R$ 0,20 a unidade e as revendeu por R$ 0,30
a unidade, ficando com uma sobra de 30 maçãs, que foram descartadas.
Indique quantas dezenas de maçãs o feirante comprou, sabendo que seu lucro
foi de R$ 30,00.
Resposta: 39
Solução:
Se n é o número de maçãs então temos 0,3(n-30) – 0,2.n = 30 , ou 0,1n=39,
que é o número de dezenas de maçãs.
23. Uma pesquisa sobre o consumo de bebida alcoólica de um grupo de 20
estudantes, em um período de 30 dias, produziu o seguinte resultado:
Número de unidades de bebida alcoólica
Número de estudantes que consumiram
De 0 a 10
12
De 11 a 20
8
Acima de 20
0
Qual o valor máximo que a média do número de unidades alcoólicas
consumidas pelos estudantes no período pode atingir?
Resposta: 14
Solução:
O valor máximo da média é (10.12+20.8)/20=14.
24. Quando x e y variam no conjunto dos números reais, qual o menor valor
assumido pelo polinômio
3x2 + 2y2 – 6x + 8y + 30 = 3(x-1)2 + 2(y+2)2 +19 ?
Resposta: 19
Solução:
O menor valor assumido pelo polinômio ocorre quando x =1 e y = -2.
25. A figura abaixo ilustra um prisma ABCDEFGH de base retangular de
dimensões 4 e 7. A face ABFE é perpendicular ao plano da base do prisma e a
o
face BCGF forma um ângulo de 30 com o plano da base do prisma. Qual o
volume do prisma , se a aresta BF mede 6?
H
G
E
F
D
A
C
B
Resposta: 84
Solução:
o
Solução: A altura do prisma é dada por BF.sen30 = 6.1/2 = 3, e o volume é
4.7.3 = 84.
26. De quantas maneiras podemos classificar os 4 empregados de uma microempresa nas categorias A ou B, se um mesmo empregado pode pertencer às
duas categorias?
Resposta: 81
Solução:
Um mesmo empregado pode ser classificado somente na categoria A,
somente na B ou em ambas. Portanto, o número de maneiras de classificar
os 4 empregados é 3.3.3.3=81.
27. Um economista apresenta proposta de trabalho às empresas X e Y, de modo
que: a probabilidade de ele ser contratado pela empresa X é de 0,61, a de ser
contratado pela empresa Y é de 0,53 e a de ser contratado pelas duas
empresas é de 0,27. Determine a probabilidade (p) de o economista não ser
contratado por nenhuma das empresas e indique 100p.
Resposta: 13
Solução:
A probabilidade de o economista ser contratado por alguma das duas
empresas é 0,61+0,53-0,27=0,87. A probabilidade de o economista não ser
contratado por nenhuma das duas empresas é p=1-0,87=0,13.
As informações seguintes referem-se às duas próximas questões.
O PIB (Produto Interno Bruto, que representa a soma das riquezas e dos serviços
produzidos por uma nação) de certo país, no ano 2000+x, é dado, em bilhões de
dólares, por
P(x) = 500+0,5x+20cos(πx/6)
onde x é um inteiro não negativo.
28. Determine, em bilhões de dólares, o valor do PIB do país em 2004 e assinale a
soma de seus dígitos.
Resposta: 15
Solução:
Para o ano 2004, temos x=4, e o valor
P(4)=500+2+20cos(2π/3)=502-10=492 bilhões de dólares.
do
PIB
será
29. Em períodos de 12 anos, o PIB do país aumenta do mesmo valor, ou seja,
P(x+12)-P(x) é constante. Determine esta constante (em bilhões de dólares).
Resposta: 6
Solução:
Temos
P(x+12)=500+0,5(x+12)+10cos(π(x+12)/6)=500+0,5x+6+10cos(πx/6)=P(x)+6.
30. O mapa abaixo representa a divisão do Brasil em suas regiões. O mapa deve
ser colorido de maneira que regiões com uma fronteira em comum sejam
coloridas com cores distintas. Determine o número (n) de maneiras de se colorir
o mapa, usando-se 5 cores. Indique n/10.
Resposta: 54
Solução:
Começando a colorir pela região centro-oeste, existem 5 cores possíveis;
passando em seguida para a região norte temos 4 cores possíveis e para as
demais regiões temos 3 cores para escolher. O total de maneiras de se colorir
o mapa é 5.4.3.3.3=540.
31. Uma pesquisa sobre a relação entre o preço e a demanda de certo produto
revelou que: a cada desconto de R$ 50,00 no preço do produto, o número de
unidades vendidas aumentava de 10. Se, quando o preço do produto era R$
1.800,00 o número de unidades vendidas era de 240, calcule o valor máximo,
em reais, que pode ser obtido com a venda das unidades do produto, e indique
a soma dos seus dígitos.
Resposta: 9
Solução:
Após x descontos de 50 reais o preço do produto será 1800-50x, e o número
de unidades vendidas será 240+10x; portanto, o total obtido com a venda
será (1800-50x)(240+10x)=500(36-x)(24+x) que assume seu máximo quando
x=(36-24)/2=6 e que tem valor máximo 1500.300=450000 reais.
32. Suponha que a taxa de juros de débitos no cartão de crédito seja de 9% ao
mês, sendo calculada cumulativamente. Em quantos meses uma dívida no
cartão de crédito triplicará de valor? (Dados: use as aproximações ln(3) ≅ 1,08
e ln(1,09) ≅ 0,09.)
Resposta: 12
Solução:
Passados t meses, a dívida passa de c para c(1+0,09)t = c1,09t e será igual a
t
3c quando 1,09 = 3 ou t = ln(3)/ln(1,09) ≅ 1,08/0,09 = 12.