A,B,C (matrizes)
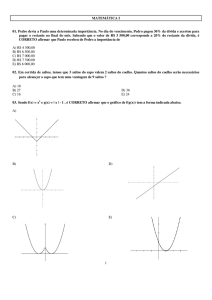
a,b,k,λ%-T.
n%0
determinante: det
D transposto: DT
D,F,G (matrizes n×n)
E (matriz elementar n×n)
A matriz D é uma matriz elementar se pode ser obtida a partir da matriz identidade de
dimensões n×n através de uma única operação elementar de linhas.
[
0
0
O= 0
⋮
0
0
0
0
⋮
0
0
0
0
⋮
0
⋱
0
0
0
⋮
0
] [
1
0
I= 0
⋮
0
0
1
0
⋮
0
0
0
1
⋮
0
⋱
0
0
0
⋮
1
]
A+B=B+A
(A+B)+C=A+(B+C)
A+O=A
A-A=O
(AB)C=A(BC)
a(bA)=(ab)A
a(AB)=(aA)B=A(aB)
AO=O
A(B+C)=AB+AC
a(A+B)=aA+aB
AIn=InA=A
A-1A=AA-1=In
((A)T)T=A
(A+B)T=AT+BT
(A-B)T=AT-BT
(kA)T=kAT
(AB)T=BTAT
Definição: Uma matriz é uma tabela rectangular ordenada de números. Os números na tabela
são chamados os elementos da matriz.
Definição: Duas matrizes são iguais se tiverem o mesmo tamanho e os seus elementos
correspondentes são iguais.
Operações com matrizes:
Seja (A)ij o elemento pertencente á linha i e coluna j da matriz A.
Definição: A+B é matriz resultante da soma de A com B, a soma de matrizes é feita de acordo
com a seguinte regra (A+B)ij=(A)ij+(B)ij.
Definição: A−B é matriz resultante da subtracção de A com B, a subtracção de matrizes é feita
de acordo com a seguinte regra (A−B)ij=(A)ij−(B)ij.
Definição: cA é a matriz resultante da multiplicação do numero c pela matriz A, a multiplicação
por um numero é feita de acordo com a seguinte regra (cA)ij=c(A)ij.
Definição: AB é a matriz resultante do produto de A com B, onde A é uma matriz com r colunas e
B uma matriz com r linhas, a multiplicação de matrizes é feita de acordo com a seguinte regra
(AB)ij=(A)i1(B)1j+(A)i2(B)2i+...+(A)ir(B)rj.
Definição: A é uma matriz m×n, a transposta de A, denotada por AT é uma matriz n×m, que é
obtida de acordo com a seguinte regra (AT)ij=(A)ji.
Definição: Seja o sistema de equações lineares Ax=b, onde x e b são vectores coluna, a matriz
A é chamada de matriz coeficiente.
Seja Ax=b um sistema de equações lineares, este sistema pode ser
a11 a 22 a 1n b 1
representado numa única matriz omitindo as várias incógnitas, isto
a 21 a 22 a 2n b 2
consiste na colocação dos elementos do vector b à direita dos
⋮
⋮ ⋱ ⋮
⋮
elementos da matriz A, tudo numa só matriz. Por exemplo:
am1 am2 amn bm
[
]
Definição(Operações elementares de linhas): As operações elementares de linhas são
operações realizadas com as linhas de uma matriz que não alteram as soluções do sistema de
equações lineares que a matriz representa. As operações elementares de linha são:
i) multiplicação de uma linha por uma constante diferente de zero
ii) troca de posição de duas linhas da matrizes
iii) soma de uma linha multiplicada por uma constante a outra linha
i)
ii)
a 11 a22 a1j
k a 11 k a 22 k a1j
a 11 a22 a1j
a21 a 22 a2j
a 21 a22 a2j a21
a 22 a 2j
a 21 a22 a2j a11 a 22 a1j
⋮
⋮ ⋱ ⋮
⋮
⋮
⋱
⋮
⋮
⋮ ⋱ ⋮
⋮
⋮ ⋱ ⋮
ai1 a i2 aij
ai1
ai2 aij
ai1 a i2 aij
ai1 ai2 aij
[
iii)
[
a 11 a22
a 21 a22
⋮
⋮
ai1 a i2
][
][
][
a1j
a11
a22
a2j a21k a11 a22 k a12
⋱ ⋮
⋮
⋮
aij
a i1
ai2
][
a1j
a 2jk a1j
⋱
⋮
aij
]
]
Definição(escada de linhas): Uma matriz em escada de linhas(row-echelon form) é uma matriz
com as seguintes três propriedades:
1) Se uma linha não é constituída apenas por zeros, então o primeiro numero diferente de zero
nessa linha é 1. Esse um é chamado de pivot.
2) Se existem linhas que são constituídas apenas por zeros, então estão todas juntas na parte
inferior da matriz.
3) Em quaisquer duas linhas sucessivas que não sejam constituídas apenas por zeros, o pivot da
linha inferior encontra-se mais à direita do que o pivot da linha superior.
Exemplo:
A resolução de um sistema de equações lineares pode ser feita numa
1 0 0 1 matriz que represente o sistema de equações. Um dos métodos para o
0 1 0 2 fazer é o método de eliminação de Gauss, que se baseia no uso de
0 0 1 3 operações elementares de linhas para colocar a matriz em escada de
0 0 0 0 linhas, de onde se pode voltar a escrever o sistema de equações numa
forma mais fácil de obter a solução do sistema.
[ ]
Definição(matriz inversa): Seja A uma matriz n×n, A−1 é a matriz inversa de A, A−1 é tal que
AA−1=I e A−1A=I(onde I é a matriz identidade). A matriz A−1 pode ser obtida da seguinte forma:
Escrever a seguinte matriz [A|I], fazer operações elementares de linhas até obter a matriz
identidade do lado esquerdo, isto é obter a matriz identidade no local onde no inicio estava a
matriz A, depois de isto feito a matriz obtida é [I|A−1].
Exemplo:
1 2 3 1 0 0
1 0 0 −40 16 9
2 5 3 0 1 0 0 1 0 13 −5 3
1 0 8 0 0 1
0 0 1
5
−2 1
[
][
]
Determinantes:
● Uma matriz A é invertível se e só se det(A)≠0
● Se D e F tem a mesma dimensão, então: det(DF)=det(D) det(F)
● Se D tem uma fila de zeros ou uma coluna de zeros, então det(D)=0
● Se D é uma matriz diagonal, triangular superior ou inferior,
então det(D)=d11d22...dnn
● Se E resulta da multiplicação de uma linha de In por k, então det(E)=k
● Se E resulta da troca de duas linhas de In, então det(E)=-1
● Se E resulta da adição de um múltiplo de uma linha de In a outra, então det(E)=1
det kD=k n detD
det DF=detDdetF
−1
SeDé invertivel, então: det D =
[
[
a 11
a12
a13
a 21b 21 a22 b 22 a 23b 23
det
a 31
a 32
a33
⋮
⋮
⋮
a i1
ai2
a i3
1
det D
][
a 1j
a11 a 12 a 13
a 2jb2j
a21 a 22 a 23
a 3j =det a31 a 32 a 33
⋱
⋮
⋮
⋮
⋮
aij
ai1 ai2 ai3
] [
[ ] [
[ ][
a11
a12
a13
ba11 ba12 ba13
det a31
a32
a33
⋮
⋮
⋮
a i1
ai2
ai3
a1j
ba1j
a3j =0
⋱ ⋮
a ij
a 11 a 12 a13
a 21 a 22 a 23
det a 31 a 32 a 33
⋮
⋮
⋮
ai1 ai2 a i3
a 11 a 12
a 21 a 22
det a 31 a 32
⋮
⋮
ai1 ai2
a13
a 23
a 33
⋮
a i3
⋱
det D=detDT
ka 11 ka 12 ka13
a21 a 22 a 23
det a31 a32 a 33
⋮
⋮
⋮
ai1
ai2
ai3
][
][
]
a1j
a11 a 12 a13
a2j
b 21 b 22 b23
a3j det a31 a 32 a33
⋱ ⋮
⋮
⋮
⋮
aij
ai1 ai2 a i3
ka1j
a 2j
a 3j =k det
⋱ ⋮
a ij
a 1j
a 21 a22 a 23
a 2j
a11 a12 a13
=−det
a 3j
a31 a32 a33
⋱ ⋮
⋮
⋮
⋮
aij
a i1 ai2 ai3
⋱
a11 a12
a 21 a22
a 31 a32
⋮
⋮
a i1 ai2
a13
a23
a33
⋮
ai3
⋱
]
⋱
a 1j
b 2j
a 3j
⋮
a ij
]
a1j
a 2j
a 3j
⋮
aij
a2j
a1j
a3j
⋮
a ij
a 1j
a11
a12
a 13
a 2j
a 21ka11 a 22ka12 a 23ka13
a 3j =det
a31
a 32
a 33
⋮
⋮
⋮
⋮
aij
ai1
ai2
ai3
a1j
a 2jka 1j
a3j
⋱
⋮
aij
]
Definição: Uma permutação de um conjunto de inteiros {1,2,...,n} é uma ordenação desses
números de uma determinada forma, tal que a ordenação seja feita sem omissões nem
repetições. Exemplo: Existem seis permutações diferentes para o conjunto de inteiros {1,2,3}.
Estas são (1,2,3), (2,1,3), (3,1,2), (1,3,2), (2,3,1), (3,2,1)
Definição: Uma permutação é chamada par se o numero total de inversões é um numero inteiro
par, e é chamada ímpar se o numero total de inversões é um numero inteiro ímpar.
Exemplo: A tabela seguinte classifica as várias permutações de {1,2,3}
Permutação
Numero de
Classificação
inversões
(1,2,3)
0
par
(1,3,2)
1
ímpar
(2,1,3)
1
ímpar
(2,3,1)
2
par
(3,1,2)
2
par
(3,2,1)
3
ímpar
Definição(Produto elementar): Por produto elementar de uma matriz A n×n pretende-se referir
qualquer produto de n elementos da matriz A, tal que nenhum dos elementos venha da mesma
coluna ou linha. Uma produto elementar é um produto da forma a1 j a 2 j ... an j , onde (j1,j2,...,jn) é
uma permutação do conjunto {1,2,...,n}.
Teorema: Uma matriz n×n tem n! produtos elementares.
1
2
n
Definição(produto elementar com sinal): Por produto elementar com sinal de uma matriz A n×n
pretende-se referir um produto elementar multiplicado por +1 ou −1, é multiplicado por +1 se
(j1,j2,...,jn) é uma permutação par e multiplicado por −1 se (j1,j2,...,jn) é uma permutação ímpar.
Definição(determinante de uma matriz): Seja A uma matriz quadrada. A função determinante é
denotada por det, e é definido por det(A) a soma de todos os produtos elementares com sinal. O
numero det(A) é chamado de determinante de A.
O determinante de A pode ser escrito simbolicamente como det A =∑ ±a1 j a2 j ... an j ,
onde 3 indica que os termos são para ser somados segundo todas as permutações (j1,j2,...,jn) e o
+ ou − é escolhido em cada parcela de acordo com a permutação ser ímpar ou par.
Definição: Se A é uma matriz quadrada, então o menor do elemento aij é denotado por Mij e é
definido como sendo o determinante da sub-matriz que resta após a remoção da linha numero i e
da coluna numero j da matriz A. O numero (−1)i+jMij é denotado por Cij e é chamado por cofactor
da entrada aij.
Teorema(expansão por cofactores): O determinante de uma matriz A n×n pode ser calculado
através da multiplicação dos elementos em qualquer linha(ou coluna) pelos seus cofactores e
somando os produtos resultantes; isto é, para cada 1AiAn e 1AjAn,
det(A)=a1jC1j+a2jC2j+...+anjCnj (expansão por cofactores ao longo da coluna numero j)
det(A)=ai1Ci1+ai2Ci2+...+ainCin (expansão por cofactores ao longo da linha numero i)
Teorema(regra de Cramer): Se ax=b é um sistema de n equações lineares com n incógnitas tal
que det(A)@0, então o sistema tem uma solução única. Esta solução é
b1
det A 1
det A 2
det An
b = b2
, x2 =
, ... , x n =
x1 =
det A
det A
det A
⋮
bn
1
2
n
[]
onde Aj é a matriz obtida pela substituição dos elementos da
coluna numero j da matriz A pelos elementos da matriz b.
Classificação de sistemas de equações lineares(SEL):
Impossíveis ou inconsistentes, se não tem soluções.
Possíveis ou consistentes:
-Determinado, se tem uma solução.
-Indeterminado, se tem infinitas soluções.
Definição: Traço de uma matriz A qualquer é a soma dos elementos da diagonal principal de A e
designa-se por tr(A).
Definição: Característica de uma matriz é o numero de linhas não nulas depois de aplicar o
método de eliminação de Gauss(MEG), denota-se por car(...).
Teorema(teorema que cresce): Seja A uma matriz n×n. Então são equivalentes as afirmações:
(a) A é invertível.
(b) O SEL Ax=0 tem apenas solução trivial.
(c) Para qualquer b, o SEL Ax=b tem sempre solução única.
(d) A pode ser expressa como produto de matrizes elementares.
(e) Car(A)=n.
(f) det(A)≠0.
Subespaços:
Teorema: U é um subespaço linear de IEn se e só se:
(ii) uv∈U ∀ u, v ∈U
(iii) ⋅u∈U ∀ u∈U,∈IE
(i) 0∈U
Definição: Um vector w é chamado de combinação linear dos vectores v1, v2, ..., vn se pode ser
expresso na forma w=k1v1+k2v2+...+knvn , onde k1, k2, ..., kn são escalares.
n
Definição: Seja v 1 , v2 ,... , vm ∈ F . Então o conjunto constituído por todas as combinações
lineares g1 v 1g 2 v 2...g m v m , onde g1 , g 2 , ..., g m ∈ F , é um subespaço de Fn. Este subespaço
é chamado de subespaço gerado por v 1 , v2 ,..., vm .
Definição: Se S={v1, v2, ..., vn} é um conjunto não-vazio de vectores, então a equação vectorial
k1v1+k2v2+...+knvn=0 tem pelo menos uma solução, nomeadamente k1=0, k2=0, ..., kn=0. Se esta é
a única solução, então S é um conjunto linearmente independente. Se existem outras soluções S
é um conjunto linearmente dependente.
Definição: Se V é um espaço qualquer e S={v1, v2, ..., vn} é um conjunto de vectores de V, então
S é uma base para V se e só se S é linearmente independente e S gera V.
Teorema: Se S={v1, v2, ..., vn} é uma base para o espaço V, então qualquer vector v em V pode
ser expresso na forma v=c1v1+c2v2+...+cnvn de apenas uma forma.
Definição: Um espaço V diferente de zero é dimensionalmente finito se contem um conjunto de
vectores finito {v1, v2, ..., vn} que formam a base. Se tal conjunto não existir, V é dimensionalmente
infinito. O espaço zero é dimensionalmente finito.
Definição: A dimensão de um espaço dimensionalmente finito V, denotado de dim(V), é o
numero de vectores de uma base para V. O espaço zero tem dimensão zero.
Espaço de soluções: O conjunto de vectores que satisfazem o sistema homogéneo Ax=0
formam um espaço chamado de espaço de soluções.
Definição: Se A é uma matriz m×n, então o subespaço de IRn gerado pelos vectores linha de A é
chamado de espaço das linhas de A, e o subespaço IRm gerado pelos vectores coluna é chamado
de espaço das colunas de A. O espaço de soluções do sistema de equações homogéneo
Ax=0,que é um subespaço de IRn, é chamado de espaço nulo de A (que é equivalente a núcleo
de A, denotado por Nuc(A)).
Teorema: Operações elementares de linhas não mudam o espaço nulo da matriz.
Teorema: Operações elementares de linhas não mudam o espaço das linhas da matriz.
Teorema: Seja A uma matriz qualquer, o espaço das linhas e o espaço das colunas de A tem a
mesma dimensão.
Definição: A dimensão comum ao espaço das linhas e ao espaço das colunas de uma matriz A é
chamado característica de A, e denotado por car(A). A dimensão do espaço nulo da A é chamado
de nulidade de A e é denotado por Nul(A).
Teorema: Seja A uma matriz qualquer, então car(A)=car(AT).
Teorema: Seja A uma matriz com n colunas, então car(A)+Nul(A)=n.
Definição: Uma função é uma regra que associa a cada elemento do domínio, um elemento do
conjunto de chegada.
Definição: Se T:V→W é uma função de um espaço vectorial V para um espaço vectorial W,
então T é chamado uma transformação linear de V para W se para todos os vectores u e v em V
e todos os escalares c
(a) T(u+v)=T(u)+T(v)
(b) T(cu)=cT(u)
No caso de V=W, a transformação linear T:V→V é chamado operador linear em V.
Definição: T:U→V é uma transformação linear, então:
Núcleo: NT={u∈U : Tu=0}⊂U
Imagem: Im T={Tu :u∈U}⊂V
Teorema: Sejam WœIRp e S={v1,v2,...vn}œIRm bases para um espaço vectorial, u um vector
pertencente a IRm, T:IRm →IRp uma transformação linear então
(T(u))W =[(T(v1))W (T(v2))W ... (T(vn))W].(u)S
Definição: Uma transformação linear T:U→V diz-se injectiva se e só se T(x)=T(y)8x=y !x,yœU
Teorema: Uma transformação linear T é injectiva se e só se Nuc(T)={0}.
Definição: Uma transformação linear T:U→V diz-se sobrejectiva se Im(T)=V.
Definição: Uma transformação linear T:U→V é bijectiva(ñisomorfismo entre U e V) se for
injectiva e sobrejectiva.
Teorema: Se T é uma transformação linear bijectiva então T-1 também é uma transformação
linear.
Definição: Seja a transformação linear T:U→U, os vectores uœU que têm a propriedade T(u)=λu
se u≠0 são chamados vectores próprios de T, os valores λ são chamados valores próprios de T e
E(λ)={uœU:T(u)=λu} o espaço próprio associado a λ.
Definição: Seja A uma matriz n×n det(A-λI) é o polinómio característico, det(A-λI)=0 a equação
característica.
Definição: A matriz quadrada A é chamada diagonalizável se existe uma matriz invertível P tal
que P-1AP é uma matriz diagonal, a matriz P é diagonalizante.
Teorema: Se A é uma matriz n×n, então as afirmações seguintes são equivalentes:
(a)A é diagonalizável, (b)A tem n vectores próprios linearmente independentes.
Teorema:Se D é uma matriz diagonal e D=P-1AP, então Ak=PDkP-1.
Procedimentos para diagonalizar uma matriz:
O teorema anterior garante que se A é uma matriz n×n com n vectores própios linearmente
independentes então é diagonalizavel.
(i) Encontrar n vectores próprios de A linearmente independentes, nomeadamente p1,p2,...,pn.
(ii) Formar a matriz P tendo p1,p2,...,pn como os seus vectores coluna.
(iii) A matriz P-1AP será então diagonal com λ1,λ2,...,λn como as suas entradas diagonais
sucessivas, onde λi é o valor próprio correspondente a pi, para i=1,2,...,n.
Definição: Chama-se espaço Euclidiano a um espaço linear com um produto interno.
Definição: O produto interno(o produto interno é designado por u•v ou <u,v>) usual designado
por u•v é dado por u•v=u1v1+u2v2+...+unvn.
Definição: Se v é um espaço Euclidiano, então a norma(ou comprimento) de um vector u um V é
denotado por ||u|| e é definido por ||u||=<u,u>1/2. A distancia entre dois pontos(vectores) u e v é
denotada por d(u,v) e é definida por d(u,v)=||u-v||.
Definição: Uma matriz quadrada com a propriedade A-1=AT é uma matriz ortogonal.
Definição: Uma matriz quadrada diz-se ortonormada se as suas colunas formarem um conjunto
ortonormado.
Teorema(Desigualdade de Cauchy-Schwarz): Se u e v são vectores de um espaço Euclidiano,
então |<u,v>|A||u|| ||v||.
Definição: Dois vectores u e v num espaço Euclidiano são ortogonais se <u,v>=0.
Definição:Seja W um subespaço de um espaço Euclidiano V. Um vector u em V é dito ser
ortogonal a W se é ortogonal a cada vector de W, e o conjunto constituído por todos os vectores
em V que são ortogonais a W é chamado de complemento ortogonal de W (W ┴).
⟨v , u⟩
v .
Teorema(Projecção de u sobre v): Pv u=
∥v∥2
Método para encontrar uma base ortogonal de vectores(Ortogonalização de GramSchmidt): Seja {v1,v2,...,vn}%IRn uma base para IRn.
w1 =v 1
w 2=v 2−Pw v 2
w3 =v 3−Pw v3 −P w v 3
⋮
1
1
2
m −1
wm =vm − ∑ P w vm
i=1
i
n
{w1,w2,...,wm} são uma base ortogonal para Ir
(u/||u|| é um vector com norma 1 e com a direcção de u).
Teorema(Melhor aproximação): Seja S um subespaço de V e v%V. Então existe um único vector
v'%S mais próximo de v do que qualquer outro vector de S. v' é exactamente a projecção
ortogonal de v sobre S. ||v-PSv||A||v-y|| !y%S (||v-PSv|| distancia de v a S).
Teorema(teorema da dimensão): Sejam U um espaço linear de dimensão finita e T uma
transformação linear que tem como espaço de partida U.
Então, o subespaço Im(T) tem dimensão finita e dim(Nuc(T))+dim(Im(T))=dim(U).
Definição: Chama-se forma quadrática(F.Q.) a uma função Q:IRn→IR que pode ser escrita na
forma Q(x)=xTAx sendo A uma matriz simétrica.
Definição: Diz-se que uma forma quadrática ou uma matriz simétrica que lhe está associada é:
1-Definida positiva se Q(x)>0, !x≠0 8 todos os valores próprios>0.
2-Definida negativa se Q(x)<0, !x≠0 8 todos os valores próprios<0.
3-Semidefinida positiva se Q(x)B0 !x 8 todos os valores própriosB0.
4-Semidefinida negativa se Q(x)A0 !x 8 todos os valores própriosA0.
5-Indefinida se Q(x) assume valores positivos e negativos 8 Uns valores próprios>0 outros<0.
Teorema: Se A é uma matiriz m×n, então:
(a)O espaço nulo de A e o espaço das linhas de A são complementos ortogonais em IRn de
acordo com o produto interno Euclidiano.
(b)O espaço nulo de AT e o espaço das colunas de A são complementos ortogonais em IRm de
acordo com o produto interno Euclidiano.
Teorema: Seja W um subespaço dimensionalmente finito do espaço Euclidiano V. Se {v1,v2,...,vr}
é uma base ortonormada para W, e u é um vector de V, então Pwu=<u,v1>v1+<u,v2>v2+...+<u,vr>vr
------------------------------------------------Apontamentos compilados por David Nuno Quelhas. Foram concretizados a partir de várias fontes de informação distintas
(Internet, Livros, slides utilizados em aulas, apontamentos pessoais). Sem desvalorizar a informação presente nestes
apontamentos, estes devem ser utilizados sempre sujeitos ao discernimento individual. Nas circunstancias em que é
necessário garantir a qualidade/exactidão da informação devem ser utilizados Livros de referencia, e/ou fontes que se saiba
serem de confiança.