FUVEST 2001

Física
ETAPA
OBSERVAÇÃO (para todas as questões de
Física): o valor da aceleração da gravidade na
superfície da Terra é representado por g.
Quando necessário adote: para g, o valor de
10 m/s2 ; para a massa específica (densidade)
da água, o valor 1.000 kg/m3 = 1 g/cm3 ; para
o calor específico da água, o valor 1,0 cal/(g.o C)
(1 caloria ≅ 4 joules). Lembre-se de que
sen 30o = cos 60o = 0,5 e sen 45o = cos 45o =
= 2 /2.
Questão 41
Da figura e da Lei da Reflexão aplicada ao espelho plano, temos:
i = r = 45 o ⇒ A = 45 o
Questão 42
Uma pessoa segura uma lente delgada junto
a um livro, mantendo seus olhos aproximadamente a 40 cm da página, obtendo a imagem
indicada na figura.
Dois espelhos planos, sendo um deles mantido na horizontal, formam entre si um ângulo
Â. Uma pessoa observa-se através do espelho
inclinado, mantendo seu olhar na direção horizontal. Para que ela veja a imagem de seus
olhos, e os raios retornem pela mesma trajetória que incidiram, após reflexões nos dois
espelhos (com apenas uma reflexão no espelho horizontal), é necessário que o ângulo Â
seja de
a) 15o
b) 30o
c) 45o
d) 60o
e) 75o
alternativa C
Para que o raio de luz retorne na horizontal, o ângulo formado entre o raio incidente (i) e o refletido
(r) deve ser de 90 o . Assim podemos montar o seguinte esquema:
Em seguida, sem mover a cabeça ou o livro,
vai aproximando a lente de seus olhos. A
imagem, formada pela lente, passará a ser
a) sempre direita, cada vez menor.
b) sempre direita, cada vez maior.
c) direita cada vez menor, passando a invertida e cada vez menor.
d) direita cada vez maior, passando a invertida e cada vez menor.
e) direita cada vez menor, passando a invertida e cada vez maior.
alternativa A
Da situação apresentada, onde a imagem é direita, menor e virtual, podemos concluir que a lente
é divergente. Assim, à medida que afastamos a
lente do objeto, obteremos uma imagem sempre
direita, virtual e cada vez menor.
FUVEST
física 2
Questão 43
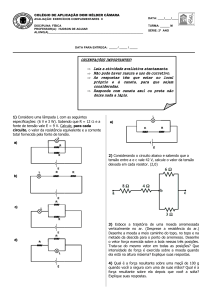
Uma peça, com a forma indicada, gira em torno de um eixo horizontal P, com velocidade
angular constante e igual a π rad/s. Uma
mola mantém uma haste apoiada sobre a
peça, podendo a haste mover-se apenas na
vertical. A forma da peça é tal que, enquanto
ela gira, a extremidade da haste sobe e desce,
descrevendo, com o passar do tempo, um movimento harmônico simples Y(t)
Segundo esse modelo, no ar, onde a velocidade de propagação do som é 340 m/s, o ouvido
humano seria mais sensível a sons com freqüências em torno de
b) 1320 Hz
a) 34 Hz
d) 3400 Hz
c) 1700 Hz
e) 6800 Hz
alternativa D
Da Equação Fundamental da Ondulatória e do
enunciado, temos:
v = λ ⋅ f ⇒ 340 = 4 ⋅ 2,5 ⋅ 10 −2 ⋅ f ⇒
⇒
Y
ETAPA
f = 3 400 Hz
Questão 45
Y
P
t
Na pesagem de um caminhão, no posto fiscal
de uma estrada, são utilizadas três balanças.
Sobre cada balança, são posicionadas todas
as rodas de um mesmo eixo. As balanças indicaram 30000 N, 20000 N e 10000 N. A partir desse procedimento, é possível concluir
que o peso do caminhão é de
como indicado no gráfico.
Assim, a freqüência do movimento da extremidade da haste será de
a) 3,0 Hz
b) 1,5 Hz
c) 1,0 Hz
d) 0,75 Hz
e) 0,5 Hz
alternativa B
O período (TP ) da peça é dado por:
2π
2π
ω =
⇒ π =
⇒ TP = 2 s
TP
TP
Como a extremidade da haste realiza 3 movimentos completos a cada volta da peça, temos:
2
3Th = TP ⇒ 3Th = 2 ⇒ Th =
s
3
Assim, a freqüência (fh ) do movimento da extremidade da haste será:
1
1
fh = 1,5 Hz
fh =
=
⇒
2
Th
3
Questão 44
Considerando o fenômeno de ressonância, o
ouvido humano deveria ser mais sensível a
ondas sonoras com comprimentos de onda
cerca de quatro vezes o comprimento do canal
auditivo externo, que mede, em média, 2,5 cm.
a) 20000 N
d) 50000 N
b) 25000 N
e) 60000 N
c) 30000 N
alternativa E
Sendo o módulo do peso (P) do caminhão igual à
soma das indicações das balanças, temos:
P = 30 000 + 20 000 + 10 000 ⇒ P = 60 000 N
Questão 46
Um mesmo pacote pode ser carregado com
cordas amarradas de várias maneiras. A situação, dentre as apresentadas, em que as
cordas estão sujeitas a maior tensão é
FUVEST
física 3
ETAPA
alternativa B
a) A
b) B
c) C
d) D
e) E
alternativa A
Na situação descrita, obtemos o seguinte esquema de forças:
Para a explosão da granada, na direção horizontal, temos:
Qantes = Qdepois ⇒ 0 = m1v1 + m 2v 2 ⇒
⇒ 0 = 2v1 + (5 − 2)v 2 ⇒ v1 = −1,5v 2
Como os dois fragmentos são lançados horizontalmente da mesma altura, o tempo de queda
(t = 10 s ) até o chão é o mesmo para ambos.
Assim, na direção horizontal, temos:
d1 = v1t ⇒ 300 = v110 ⇒ v1 = 30 m/s.
Como v1 = −1,5 v 2 ⇒ v 2 = −20 m/s.
Assim, a parte da energia liberada na explosão,
que é transformada em cinética dos fragmentos, é
dada por:
1
1
EC =
mv2 +
m 2v 22 ⇒
2 1 1
2
1
1
⇒ EC =
⋅ 2 ⋅ 30 2 +
⋅ 3( −20) 2 ⇒
2
2
⇒
E C = 1 500 J
Questão 48
No equilíbrio (R = 0 ), temos:
P
2 T cosθ = P ⇒ T =
2 cosθ
A tensão (T) será a maior para o menor cosθ, o
que ocorre para a situação onde o ângulo entre
os fios é o maior, correspondendo à alternativa A.
Uma prancha rígida, de 8 m de comprimento,
está apoiada no chão (em A) e em um suporte
P, como na figura. Uma pessoa, que pesa metade do peso da prancha, começa a caminhar
lentamente sobre ela, a partir de A. Pode-se
afirmar que a prancha desencostará do chão
(em A), quando os pés dessa pessoa estiverem
à direita de P, e a uma distância desse ponto
aproximadamente igual a
Questão 47
Uma granada foi lançada verticalmente, a
partir do chão, em uma região plana. Ao atingir sua altura máxima, 10 s após o lançamento, a granada explodiu, produzindo dois fragmentos com massa total igual a 5 kg, lançados horizontalmente. Um dos fragmentos,
com massa igual a 2 kg, caiu a 300 m, ao Sul
do ponto de lançamento, 10 s depois da explosão. Pode-se afirmar que a parte da energia
liberada na explosão, e transformada em
energia cinética dos fragmentos, é aproximadamente de
a) 900 J
b) 1 500 J
c) 3 000 J
d) 6 000 J
e) 9 000 J
a) 1,0 m
d) 2,5 m
b) 1,5 m
e) 3,0 m
c) 2,0 m
alternativa C
Na iminência da prancha desencostar do chão, o
esquema de forças na prancha é dado por:
FUVEST
física 4
No equilíbrio, temos:
M R(P) = O ⇒ |P| ⋅ cosθ ⋅ 1 =
⇒
|P|
⋅ cosθ ⋅ d ⇒
2
d=2m
ETAPA
mo corpo na superfície da Terra, é aproximadamente de
a) 0,02
b) 0,05
c) 0,10
d) 0,50
e) 0,90
alternativa E
Questão 49
Para pesar materiais pouco densos, deve ser
levado em conta o empuxo do ar. Define-se,
nesse caso, o erro relativo como
Erro relativo =
Peso real – Peso medido
Peso real
Em determinados testes de controle de qualidade, é exigido um erro nas medidas não superior a 2%. Com essa exigência, a mínima
densidade de um material, para o qual é possível desprezar o empuxo do ar, é de
a) 2 vezes a densidade do ar
b) 10 vezes a densidade do ar
c) 20 vezes a densidade do ar
d) 50 vezes a densidade do ar
e) 100 vezes a densidade do ar
Da Lei da Gravitação Universal, temos:
GMT ⋅ mC
Fe
(1,05RT ) 2
=
GM
F
T ⋅ mC
(RT ) 2
⇒
⇒
Fe
RT2
=
⇒
F
(1,05) 2 ⋅ RT2
Fe
= 0,90
F
Questão 51
Um motociclista de motocross move-se com
velocidade v = 10 m/s, sobre uma superfície
plana, até atingir uma rampa (em A), inclinada de 45o com a horizontal, como indicado na
figura.
alternativa D
Como a diferença entre o peso real e o peso medido é devido ao empuxo, para um erro nas medidas não superior a 2%, temos:
Peso real − Peso medido
2
≥
⇒
100
Peso real
d Vg
Empuxo
2
2
⇒
≥
⇒
≥ ar
⇒
100
Peso real
100
dmat .Vg
100
⇒ dmat . ≥ 50 dar
2
Portanto, a mínima densidade do material, para
que seja possível desprezar o empuxo do ar, é de
50 vezes a densidade do ar.
⇒ dmat . ≥ dar ⋅
Questão 50
A Estação Espacial Internacional, que está
sendo construída num esforço conjunto de diversos países, deverá orbitar a uma distância
do centro da Terra igual a 1,05 do raio médio
da Terra. A razão R = Fe/F, entre a força Fe
com que a Terra atrai um corpo nessa Estação e a força F com que a Terra atrai o mes-
A trajetória do motociclista deverá atingir novamente a rampa a uma distância horizontal
D (D=H), do ponto A, aproximadamente igual
a
a) 20 m
b) 15 m
c) 10 m
d) 7,5 m
e) 5 m
alternativa A
Considerando o movimento do motociclista como
um lançamento horizontal, temos:
H
1 2
1
.
∆y =
gt ⇒ H =
⋅ 10t 2 ⇒ t =
5
2
2
Como na horizontal o movimento é uniforme e sabendo que D = H, temos:
H
D
∆x = v ⋅ t ⇒ D = 10 ⋅
⇒ D = 10
⇒
5
5
⇒ D 2 = 100 ⋅
D
⇒
5
D = 20 m
FUVEST
física 5
ETAPA
Questão 52
Dois caixotes de mesma altura e mesma massa, A e B, podem movimentar-se sobre uma
superfície plana, sem atrito. Estando inicialmente A parado, próximo a uma parede, o caixote B aproxima-se perpendicularmente à parede, com velocidade V0 , provocando uma sucessão de colisões elásticas no plano da figura.
Após todas as colisões, é possível afirmar que
os módulos das velocidades dos dois blocos serão aproximadamente
a) VA = V0 e VB = 0
b) VA = V0 /2 e VB = 2 V0
c) VA = 0 e VB = 2 V0
d) VA = V0 / 2 e VB = V0 / 2
e) VA = 0 e VB = V0
alternativa E
Como A e B têm a mesma massa e o choque é
central, direto e elástico, as velocidades serão trocadas, ou seja, VA = V0 e VB = 0 .
Como a parede é fixa e o choque entre A e a parede também é central, direto e elástico, o módulo
da velocidade de A será mantido, ou seja, A voltará com velocidade VA = V0 .
Na nova colisão entre A e B ocorrerá novamente
troca de velocidades, ou seja, VA = 0 e VB = V0 .
Questão 53
O processo de pasteurização do leite consiste
em aquecê-lo a altas temperaturas, por alguns segundos, e resfriá-lo em seguida. Para
isso, o leite percorre um sistema, em fluxo
constante, passando por três etapas:
I) O leite entra no sistema (através de A), a
5o C, sendo aquecido (no trocador de calor B)
pelo leite que já foi pasteurizado e está saindo do sistema.
II) Em seguida, completa-se o aquecimento
do leite, através da resistência R, até que ele
atinja 80o C. Com essa temperatura, o leite retorna a B.
III) Novamente em B, o leite quente é resfriado pelo leite frio que entra por A, saindo do
sistema (através de C), a 20o C.
Em condições de funcionamento estáveis, e
supondo que o sistema seja bem isolado termicamente, pode-se afirmar que a temperatura indicada pelo termômetro T, que monitora a temperatura do leite na saída de B, é
aproximadamente de
a) 20o C
b) 25o C
c) 60o C
o
o
d) 65 C
e) 75 C
alternativa D
Em condições de funcionamento estáveis, e supondo que o sistema seja bem isolado termicamente, ocorre troca de calor somente entre o leite
frio e o aquecido (Qfrio + Qaquecido = 0 ).
Como o sistema opera em fluxo constante, em
um mesmo intervalo de tempo, a massa do leite
frio é igual à massa do leite aquecido no trocador
de calor B. Dessa forma, temos:
Qfrio + Qaquecido = 0 ⇒
⇒ mf ⋅ c ⋅ ∆θf + maq ⋅ c ⋅ ∆θaq = 0 ⇒
⇒ ∆θf + ∆θaq = 0 ⇒
⇒ ( θ − 5) + (20 − 80) = 0 ⇒
θ = 65 o C
Questão 54
Em uma panela aberta, aquece-se água, observando-se uma variação da temperatura da
água com o tempo, como indica o gráfico. Desprezando-se a evaporação antes da fervura,
em quanto tempo, a partir do começo da ebulição, toda a água terá se esgotado? (Considere que o calor de vaporização da água é cerca
de 540 cal/g)
a) 18 minutos
c) 36 minutos
e) 54 minutos
b) 27 minutos
d) 45 minutos
FUVEST
física 6
ETAPA
alternativa E
Supondo o fluxo de calor (Φ) da fonte constante,
temos:
∆Qa
∆Qe
Φaquecimento = Φebulição ⇒
=
⇒
∆ta
∆te
m ⋅ c ⋅ ∆θa
1 ⋅ (70 − 30)
m ⋅L
=
⇒
=
⇒
(5 − 1)
∆ta
∆te
=
540
⇒
∆te
∆te = 54 min
Questão 55
Um gás, contido em um cilindro, à pressão atmosférica, ocupa um volume V0 ,
à temperatura ambiente
T0 (em kelvin). O cilindro
contém um pistão, de
massa desprezível, que
pode mover-se sem atrito e que pode até, em
seu limite máximo, duplicar o volume inicial
do gás. Esse gás é aquecido, fazendo com que
o pistão seja empurrado ao máximo e também com que a temperatura do gás atinja
quatro vezes T0 . Na situação final, a pressão
do gás no cilindro deverá ser
a) metade da pressão atmosférica
b) igual à pressão atmosférica
c) duas vezes a pressão atmosférica
d) três vezes a pressão atmosférica
e) quatro vezes a pressão atmosférica
a) mesma direção e intensidade.
b) direções diferentes e mesma intensidade.
c) mesma direção e maior intensidade em I.
d) direções diferentes e maior intensidade
em I.
e) direções diferentes e maior intensidade
em II.
alternativa B
A intensidade do vetor campo elétrico é inversamente proporcional ao quadrado da distância das
cargas ao ponto P. Assim, como as cargas das
esferas são iguais, se uma esfera que está a uma
distância d do ponto P produz campo de intensidade 4E, a esfera que está a uma distância 2d
produz campo de intensidade E. Admitindo as
cargas positivas, temos:
alternativa C
Da Equação Geral dos Gases, vem:
p0V0
p V
p ⋅ 2V0
pV
=
⇒ 0 0 =
⇒
T0
T
T0
4T0
p = 2p0
Questão 56
Duas pequenas esferas, com cargas elétricas
iguais, ligadas por uma barra isolante, são
inicialmente colocadas como descrito na situação I. Em seguida, aproxima-se uma das esferas de P, reduzindo-se à metade sua distância até esse ponto, ao mesmo tempo em que
se duplica a distância entre a outra esfera e
P, como na situação II. O campo elétrico em
P, no plano que contém o centro das duas esferas, possui, nas duas situações indicadas,
Portanto, o vetor campo elétrico resultante (E R )
nas duas situações indicadas tem direções diferentes e mesma intensidade.
Obs.: caso admitíssemos as cargas negativas, teríamos campos resultantes em sentidos opostos.
A resposta da questão, no entanto, seria a mesma.
FUVEST
física 7
Questão 57
Dispondo de pedaços de fios e 3 resistores de
mesma resistência, foram montadas as conexões apresentadas abaixo. Dentre essas,
aquela que apresenta a maior resistência elétrica entre seus terminais é
a)
ETAPA
Desprezando efeitos dissipativos, o conjunto
de todos os gráficos que podem representar a
velocidade V do ímã A, em função da posição
x de seu centro P, é constituído por
a) II
b) I e II
c) II e III
d) I e III
e) I, II e III
alternativa D
Quando o ímã cilíndrico A aproxima-se do ímã B
surge uma força resultante de repulsão magnética. Se esta força for muito intensa, é capaz de superar a inércia do movimento do ímã A, diminuindo sua velocidade até parar, fazendo o mesmo
voltar para a esquerda, como mostra o gráfico I.
Se a força resultante de repulsão magnética não
for capaz de superar a inércia do movimento do
ímã A, este continuará indo da esquerda para a
direita com sua velocidade variando de acordo
com a proximidade dos pólos sul e norte do ímã A
com o ímã B, como mostra o gráfico III.
b)
c)
d)
Questão 59
e)
Um circuito doméstico simples, ligado à rede
de 110 V e protegido por um fusível F de 15 A,
está esquematizado abaixo.
alternativa C
Para obtermos a maior resistência equivalente,
devemos associar o máximo de resistores em série, o que corresponde à situação da alternativa C.
Questão 58
Um ímã cilíndrico A, com um pequeno orifício
ao longo de seu eixo, pode deslocar-se sem
atrito sobre uma fina barra de plástico horizontal. Próximo à barra e fixo verticalmente,
encontra-se um longo ímã B, cujo pólo S encontra-se muito longe e não está representado na figura. Inicialmente o ímã A está longe
do B e move-se com velocidade V, da esquerda para a direita.
A potência máxima de um ferro de passar
roupa que pode ser ligado, simultaneamente,
a uma lâmpada de 150 W, sem que o fusível
interrompa o circuito, é aproximadamente de
a) 1100 W
b) 1500 W
c) 1650 W
d) 2250 W
e) 2500 W
alternativa B
A potência máxima (P) a ser fornecida pela rede,
devido ao fusível F, pode ser calculada por:
P = Ui = 110 ⋅ 15 ⇒ P = 1 650 W
Esse valor compreende a potência da lâmpada
(150 W) e a potência máxima do ferro (P’). Portanto, temos:
P’ = 1 650 − 150 ⇒
P’ = 1 500 W .
FUVEST
física 8
Questão 60
Três fios verticais e muito longos atravessam
uma superfície plana e horizontal, nos vértices de um triângulo isósceles, como na figura
abaixo desenhada no plano.
Por dois deles ( • ), passa uma mesma corrente que sai
do plano do papel e pelo terceiro ( X ), uma
corrente que entra nesse plano. Desprezando-se os efeitos do campo magnético terrestre, a direção da agulha de uma bússola, colocada eqüidistante deles, seria melhor representada pela reta
a) A A’
b) B B’
c) C C’
d) D D’
e) perpendicular ao plano do papel.
ETAPA
alternativa A
Assumindo que as direções BB’ e DD’ são perpendiculares entre si e aplicando-se a regra da
mão direita, podemos indicar o vetor campo magnético criado por cada uma das correntes no ponto do plano eqüidistante destas através da figura
a seguir:
Projetando-se esses vetores nas direções AA’ e
CC’, verificamos que as componentes em CC’ se
equilibram. Portanto, o vetor campo magnético resultante possui a direção AA’, direção esta assumida pela agulha da bússola.
Obs.: se não considerarmos as direções BB’ e
DD’ perpendiculares entre si, teremos uma alteração no desenho, porém sem afetar a resposta.