Apresentação do PowerPoint

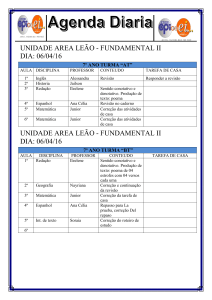
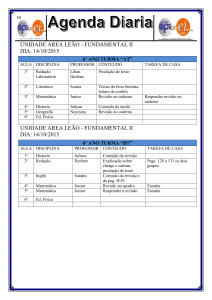
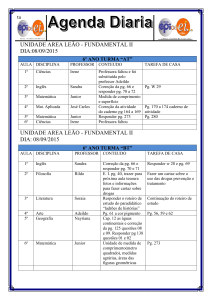
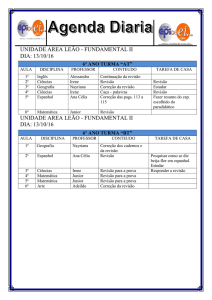
Aula
13/03/2012
CEL033
Circuitos Lineares I
NR-10
Prof.: Ivo Chaves da Silva Junior
[email protected]
Prof.: Ivo Chaves da Silva Junior
Site Disciplina
NR-10
www.ufjf.br/ivo_junior
Prof.: Ivo Chaves da Silva Junior
CEL033_NOTURNO
NR-10
Prof.: Ivo Chaves da Silva Junior
Teoria do Circuitos Elétricos
(Alessandro Volta – Físico Italiano – 1745 -1827 )
1800- Invenção da Bateria Elétrica (Pilha de Volta).
Possibilitou o fluxo contínuo de energia e conseqüentemente a construção de
circuitos elétricos.
Circuito Elétrico:
NR-10
Interligação entre dispositivos elétricos de modo a orientar o fluxo de
energia (corrente) para uma determinada finalidade.
Prof.: Ivo Chaves da Silva Junior
Circuito Elétrico (exemplo):
POSSÍVEIS COMPONENTES DE UM CIRCUITO ELÉTRICO
PERGUNTA:
Como surge a corrente ?
Corrente
elétrica
NR-10
Ch1 e/ou Ch2 FECHADAS
Circuito Elétrico Real
Esquema Representativo
(modelo)
Prof.: Ivo Chaves da Silva Junior
ÁTOMO
NÚCLEO :
PRÓTONS + NÊUTRONS
Carga (+)
Carga (nula)
q  1,602 1019 (Coulombs)
ELETROSFERA NR-10
:
ELÉTRONS
Carga (-)
q  1,602 1019 (Coulombs)
Prof.: Ivo Chaves da Silva Junior
ÁTOMO
COM POUCOS ELÉTRONS NA ÚLTIMA
CAMADA SÃO CONDUTORES.
TÊM FACILIDADE DENR-10
PERDER
ELÉTRONS.
Prof.: Ivo Chaves da Silva Junior
MATERIAL CONDUTOR
Os elétrons ficam constantemente trocando de átomos (movimento
desordenado).
NR-10
Prof.: Ivo Chaves da Silva Junior
Se polarizarmos as extremidades do material condutor
-
+
NR-10
Movimento Ordenado dos Elétrons
CORRENTE ELÉTRICA
Prof.: Ivo Chaves da Silva Junior
+
As cargas se
movimentam em todas
as direções. Porem, não
temos corrente elétrica.
Polarização
polarização
NR-10
Corrente elétrica
Prof.: Ivo Chaves da Silva Junior
CORRENTE ELÉTRICA
É o movimento ordenado de cargas elétricas (Elétrons)
A colisão dos elétrons com partículas do
material condutor
produz
CALOR e/ou LUZ
Lei de Joule
(também conhecida como efeito Joule) é uma lei física
que expressa a relação entre o calor gerado e a corrente
elétrica que percorre um condutor em determinado
NR-10
tempo. O nome é devido a James Prescott Joule (18181889) que estudou o fenômeno em 1840.
James Prescott Joule (Salford, 24 de dezembro de 1818 — Sale, Trafford,
11 de outubro de 1889) - físico britânico.
Prof.: Ivo Chaves da Silva Junior
EFEITO JOULE
NR-10
Prof.: Ivo Chaves da Silva Junior
Redução da
Lucratividade
Perdas na Distribuição
de Energia Elétrica
Efeito Joule
Elevam a quantidade
de energia comprada
pelas concessionárias
Efeito Joule
Furtos
NR-10
Prof.: Ivo Chaves da Silva Junior
Pergunta:
Qual é o sentido da corrente elétrica pelo condutor ?
Corrente associada ao movimento das cargas negativas (Elétrons).
Teoria dos circuitos (1800 – Alessandro Volta):
Corrente associada ao movimento das cargas positivas (convenção).
(Sentido Real: Elétrons)
Corrente Sentido Convencional
( Teoria dos Circuitos)
NR-10
(Sentido Convencional: Prótons)
Teoria de circuitos
Prof.: Ivo Chaves da Silva Junior
i
i
+
Sentido real da
corrente
Sentido
convencional
da corrente
NR-10
+
-
+
Prof.: Ivo Chaves da Silva Junior
SÉRIE FRANCESA - VIAGEM NO NUNDO DA ELETRICIDADE
NR-10
Prof.: Ivo Chaves da Silva Junior
Cálculo da Corrente Elétrica Média
(-)
(+)
q(t )
i(t ) 
t
(Coulomb/segundo)
(ampères)
Corte transversal no condutor
Cálculo da Corrente Elétrica Instantânea
q(t )
i(t ) 
t 0
t
NR-10
dq(t )
i (t ) 
dt
(ampères)
Taxa de variação da carga em
relação ao tempo
Prof.: Ivo Chaves da Silva Junior
As correntes elétricas podem ser classificadas de acordo com o seu
comportamento temporal:
Invariante no Tempo
NR-10
Variante no Tempo
Variante no Tempo
Média não nula
Média nula
Prof.: Ivo Chaves da Silva Junior
Medição da Corrente
Amperímetro
NR-10
Simbologia:
Prof.: Ivo Chaves da Silva Junior
Cálculo da Quantidade de Carga
dq(t )
Vimos que a corrente elétrica instantânea: i (t ) 
dt
Reescrevendo a equação (I):
(I)
dq(t )  i(t )  dt
(II)
Integrando a equação (II) em relação ao tempo, tem-se:
t2
q   i (t )  dt
NR-10
q
t1
Prof.: Ivo Chaves da Silva Junior
Exercício 1 :
Encontre o valor da carga (q) que entrou no terminal de um elemento
entre t=zero e t=3 segundos, sendo que a corrente no elemento é dada
pelo gráfico abaixo.
Memória
t2
q   i (t )  dt
t1
NR-10
Resp: q=5 C
Prof.: Ivo Chaves da Silva Junior
Integral
3
1
3
2
t
q   i(t )  dt   1 dt   t  dt  t |10  |13  5C
2
0
0
1
NR-10
Área
(1  3)  2
q   i(t )  dt  (11) 
 5C
2
0
3
Prof.: Ivo Chaves da Silva Junior
Exemplos
Níveis de Corrente Elétrica (Ampères)
NR-10
Prof.: Ivo Chaves da Silva Junior
Bipolos Elétricos
Dispositivos elétricos com dois terminais de acesso (A-B) através do qual
pode circular corrente elétrica.
+
+
-
-
Exemplos:
• resistores;
• capacitores;
• indutores;
NR-10
• geradores;
• diodos;
• etc.
Prof.: Ivo Chaves da Silva Junior
Cálculo da Diferença de Potencial (ddp) ou Tensão (v)
A passagem de corrente resulta de uma diferença de potencial (ddp - tensão)
entre os terminais + e
-.
Essa diferença de potencial (ddp) é dada pela taxa de variação da energia
“w” (Joule) necessária para deslocar uma carga unitária “q” (Coulomb) de
um ponto à outro.
dw(t )
v(t ) 
dq(t )
(Joule/Coulomb)
(Volts)
Taxa de
variação
NR-10
da energia (w) em
relação a carga (q)
Prof.: Ivo Chaves da Silva Junior
Diferença de Potencial (ddp) ou Tensão (v)
v AB  5 Volts
Ponto “A” está 5 V acima do ponto “B”
vBA  5 Volts
Ponto “B” está 5 V abaixo do ponto “A”
NR-10
• Ambos os exemplos representam a mesma tensão : 5 volts
• O sinal (+/-) representa apenas o sentido da tensão
( maior potencial  menor potencial)
Prof.: Ivo Chaves da Silva Junior
Medição da Tensão
Voltímetro
NR-10
Simbologia:
Prof.: Ivo Chaves da Silva Junior
Exemplos
Níveis de Tensão Elétrica (Volts)
NR-10
Prof.: Ivo Chaves da Silva Junior
Cálculo da Potência Elétrica Instantânea (p)
Defini-se Potência Elétrica como a velocidade com que uma energia
elétrica é dissipada. Ou seja:
Taxa de variação da energia
em relação ao tempo
Sabe-se que:
dw(t )
p(t ) 
dt
dw(t )
dq(t )
v(t ) 
i (t ) 
dq(t )
dt
(Joule/s)
(Watt)
NR-10
Manipulando as equações acima, tem-se :
Prof.: Ivo Chaves da Silva Junior
dw(t )  v(t )  dq(t )
dw(t )
p(t ) 
dt
dq(t )
dt 
i (t )
v(t )  dq(t )
p(t ) 
 v(t )  i (t )
 dq(t ) 
i (t ) 

NR-10
Prof.: Ivo Chaves da Silva Junior
Potência Elétrica Instantânea é dada por:
p(t )  v(t )  i(t )
(Watts)
Pergunta
A Potência Elétrica está sendo Fornecida ou Consumida? Como saber?
Convenção do Gerador
Convenção do Receptor
v(t )  i (t )  0
Fornece
v(t )  i (t )  0
Consome
v(t )  i (t )  0NR-10
Consome
v(t )  i (t )  0
Fornece
Prof.: Ivo Chaves da Silva Junior
Cálculo da Energia Elétrica (w)
Defini-se Energia Elétrica como a quantidade de potência elétrica
fornecida ou consumida em um determinado intervalo de tempo.
dw(t )
p(t ) 
dt
(watt)
dw(t )  p(t )  dt
(III)
Integrando a equação (III) em relação ao tempo, tem-se:
Energia Elétrica (w)
t2
w   p(t )  dt
NR-10
(watt . s)
(Joule)
w
t1
Prof.: Ivo Chaves da Silva Junior
Energia Elétrica
t2
W   p(t )  dt
(Joules)
t1
Medidor Residencial de Energia
(kWh)
NR-10
1 kWh  3,6 10 joules
6
Prof.: Ivo Chaves da Silva Junior
Exercício 2 :
Qual a energia transferida a um bipolo durante o intervalo de tempo de 0
a 10s, dado que a potência consumida é a descrita pelo gráfico abaixo.
Memória
t2
w   p(t )  dt
t1
NR-10
Resp: w=150 J
Prof.: Ivo Chaves da Silva Junior
NR-10
Prof.: Ivo Chaves da Silva Junior
Integração Numérica
Com base no gráfico abaixo
responda: Qual o valor da
energia (Joule) transferida a um
bipolo entre 5 e 10 segundos?
Integração Simbólica
NR-10
Prof.: Ivo Chaves da Silva Junior
Os bipolos elementares podem ser de dois tipos:
PASSIVOS: Não introduzem energia contínua ao sistema
ATIVOS : introduzem energia contínua ao sistema
NR-10
Sendo ainda classificados em relação corrente/tensão em:
LINEARES E NÃO LINEARES
Prof.: Ivo Chaves da Silva Junior
Bipolos Passivos
RESISTOR
CAPACITOR
CONSOME ENERGIA
ARMAZENA ENERGIA
Campo Elétrico
NR-10
INDUTOR
ARMAZENA ENERGIA
Campo Magnético
Prof.: Ivo Chaves da Silva Junior
Bipolos Passivos
Resistores
Resistência Elétrica (R):
Propriedade de um determinado material se opor ao movimento
dos elétrons.
Resistor:
Bipolo elementar cuja característica predominante é resistiva.
Simbologia:
NR-10
Unidade: Ohms (Ω)
Prof.: Ivo Chaves da Silva Junior
Bipolos Passivos
Resistores
Resistores de Filme de Carbono (+ comuns e baratos)
Utilização de resistores:
NR-10
• Produção de Calor (Efeito Joule)
• Limitador de Corrente (Ligação em paralelo)
• Divisores de Tensão (Ligação em série)
Prof.: Ivo Chaves da Silva Junior
Bipolos Passivos
Resistores
Resistor de Filme de Carbono – Leitura da Resistência
NR-10
Prof.: Ivo Chaves da Silva Junior
Bipolos Passivos
Resistores
Exemplos:
NR-10
Prof.: Ivo Chaves da Silva Junior
Bipolos Passivos
Resistores
1821 – Artigo: “ A Corrente Galvânica,
tratada matematicamente”
RELAÇÃO TENSÃO E CORRENTE
EM UM RESISTOR – LEI DE OHM
NR-10
LEI DE OHM
A tensão entre os terminais de uma resistência é diretamente
proporcional à corrente que a atravessa.
Prof.: Ivo Chaves da Silva Junior
Bipolos Passivos
Resistores
A equação que rege a LEI DE OHM é dada por:
v(t )  R  i(t )
Resistor ideal
Resistência Constante
Outra grandeza muito utilizada é a condutância (G)
1
G
R
1
Unidade: Siemens (s ) /mho ( )
NR-10
A LEI DE OHM pela condutância é dada por:
i(t )  G  v(t )
Prof.: Ivo Chaves da Silva Junior
Bipolos Passivos
Resistores
Característica Tensão-Corrente (resistor ideal)
NR-10
RELAÇÃO LINEAR
ENTRE TENSÃO E CORRENTE
Prof.: Ivo Chaves da Silva Junior
Bipolos Passivos
Resistores
Cálculo da Resistência (R)
l
R
A
  resistividade (.m)
l  largura(m)
A  área(m 2 )
Varia com a
NR-10 !!!
Temperatura
Prof.: Ivo Chaves da Silva Junior
Bipolos Passivos
Resistores
A lei de Ohm é válida para resistências não lineares?
Não. Resistências não lineares não seguem a LEI DE OHM
(tensão e corrente não são diretamente proporcionais)
Não Linearidades decorrentes de:
Temperatura – Luminosidade – Umidade - etc...
Resistividade (Tungstênio)
  4,6  0,02T  1,85 10 T
6
NR-10
2
Variação com o quadrado da temperatura (T)
Prof.: Ivo Chaves da Silva Junior
Bipolos Passivos
Resistores
Característica Tensão-Corrente (resistor real)
NR-10
RELAÇÃO NÃO LINEAR
ENTRE TENSÃO E CORRENTE
Prof.: Ivo Chaves da Silva Junior
Bipolos Passivos
Resistores
NR-10
Prof.: Ivo Chaves da Silva Junior
Bipolos Passivos
Resistores
Observação
Na realidade todos os resistores são não lineares, porque as
características elétricas são afetadas por fatores externos
(principalmente temperatura e umidade). Entretanto, em
determinadas regiões aproximam do comportamento
linear, sendo estas as regiões consideradas na análise
dos circuitos elétricos.
Comportamento
próximo do LINEAR
NR-10
Prof.: Ivo Chaves da Silva Junior
Bipolos Passivos
Resistores
NR-10
Prof.: Ivo Chaves da Silva Junior
Bipolos Passivos
Resistores
Dois valores extremos importantes de resistência são:
v  Ri
Curto- Circuito
Corrente máxima
i
v
R0
Tensão nula
R
R
Circuito-AbertoNR-10
Tensão máxima
Corrente Nula
Prof.: Ivo Chaves da Silva Junior
Bipolos Passivos
Resistores
Potência Elétrica
Lei de Ohm
p(t )  v(t )  i(t )
v(t )  R  i(t )
Cálculo da Potência Elétrica Dissipada em um Resistor
p(t )  R  i(t )  i(t )  R  i (t )
2
Característica
2
v(t ) v (t )
p(t )  v(t ) 

R
R
Não-Linear
NR-10
Prof.: Ivo Chaves da Silva Junior
Exercícios
Quadro Negro
NR-10
Prof.: Ivo Chaves da Silva Junior