Magnetron: Do radar ao forno de microondas

Pró-Reitoria de Graduação
Curso de Física
Trabalho de Conclusão de Curso
MAGNETRON: DO RADAR AO FORNO DE MICRO-ONDAS
Autor: Karla Susane Borges dos Santos
Orientador: Dr. Sérgio Luiz Garavelli
Co-orientador: Dr. Armando M. Maroja
Brasília - DF
2011
1
Magnetron: Do Radar ao forno de micro-ondas
(Magnetron: From radar to the microwave)
Karla S. B. Santos1, Armando M. Maroja2, Sérgio L. Garavelli1
1
(Curso de Física - Universidade Católica de Brasília)
( Departamento de Física – Universidade de Brasília – co-orientador)
1
(Curso de Física - Universidade Católica de Brasília - orientador)
2
A solução de um problema apresentado num livro didático motivou o
aprofundamento do estudo sobre o funcionamento de um magnetron, que é o gerador
das micro-ondas de um forno. Neste trabalho são apresentados os princípios físicos
de funcionamento de um magnetron e também os princípios de funcionamento de um
forno de micro-ondas. Através da análise e medidas das dimensões dos componentes
de um magnetron retirado de um forno real é estimada a freqüência de operação de
um forno.
Palavras-chave: Magnetron, forno de micro-ondas.
The solution of a problem presented in a textbook motivated a deeper study on
the operation of a magnetron, which is the generator of a microwave oven. This paper
presents the physical principles of operation of a magnetron and also the principles of
operation of a microwave oven. Through the analysis and measurements of the
dimensions of the components of an oven magnetron taken from a real is estimated the
frequency of operation of a furnace.
Keywords: Magnetron, microwave oven.
1.
Introdução
Magnetron
O magnetron é uma válvula que gera micro-ondas, que são ondas
eletromagnéticas, com comprimentos de onda de 1 mm a 1 m. As micro-ondas
estão no espectro eletromagnético entre as ondas de rádio e infravermelho.
Corresponde à freqüências de 300 MHz até 300 GHz.
O primeiro Magnetron, que tornou possível o radar de micro-ondas foi na
Segunda Guerra Mundial e continha oito cavidades ressonantes (PURCELL,
1973).
O radar (detecção e localização por rádio) foi o primeiro aparelho
tecnológico prático para a utilização da radiação na faixa das micro-ondas. O
radar foi desenvolvido para a Segunda Guerra Mundial, com o objetivo da
navegação aérea e da localização de aeronaves inimigas da época. A
freqüência designada dos radares está entre 5 GHz e 6 GHz (CARVALHO,
2005).
2
O forno de micro-ondas foi desenvolvido durante a Segunda Guerra
Mundial quando alguns pesquisadores americanos que trabalhavam com a
construção de radares, perceberam que as micro-ondas também eram capazes
de aquecer e cozinhar os alimentos colocados próximos à fonte de emissão de
radiação. Essa descoberta proporcionou a construção de fornos experimentais,
que na época eram grandes e muito caros. Esses foram a base para o
desenvolvimento dos fornos domésticos atuais (CARVALHO, 2005).
O estudo dos radares proporcionou esclarecimentos sobre as microondas, embora tenha sido desenvolvida essa tecnologia para a transmissão de
informações, a partir de 1940 o estudo desenvolvido, utilizando as micro-ondas,
gerou aplicações que estão presentes atualmente na sociedade. Como por
exemplo, no radar, no forno de micro-ondas, nas telecomunicações, na
medicina, na indústria e várias outras (CARVALHO, 2005).
A freqüência mais utilizada é a de 2,45 GHz encontrada em fornos
domésticos, no entanto os fornos industriais operam com freqüências, de 13,56
MHz, 896 MHz e 24,12 MHz (CARVALHO, 2005).
2.
A física do Magnetron
Um circuito elétrico formado por uma bateria
 , uma bobina L e um
capacitor C forma um circuito oscilante. Devido a processos sucessivos de
carga e descarga do capacitor é possível produzir a variação do campo
elétrico. Quando o capacitor está carregado existe um campo elétrico entre
suas placas condutoras; na descarga do capacitor acontece uma diminuição da
sua intensidade e logo aparece um campo magnético induzido e a corrente que
percorre a bobina, esse campo magnético é crescente. Quando o capacitor fica
descarregado, o campo elétrico fica nulo e o campo magnético que apareceu
chega ao seu valor máximo. As sucessivas cargas e descargas do capacitor
junto com os campos elétricos e magnéticos oscilantes que se reconstroem
várias vezes, formam as ondas eletromagnéticas.
Foi James Clark Maxwell um físico e matemático britânico, que afirmou
que cargas elétricas oscilantes ou aceleradas geram ondas eletromagnéticas
capazes de transportar energia (MAI, et. al., 2008).
As freqüências das ondas eletromagnéticas dependem das propriedades
do capacitor e da bobina. O tempo para que aconteça a carga e a descarga do
3
capacitor é diretamente proporcional à sua capacitância. E a energia
armazenada na bobina depende da indutância.
Figura 01 – Modelo de oscilador elétrico (MAI, et. al., 2008).
A Figura 01 (a) mostra um circuito oscilante formado por um capacitor de
placas paralelas, uma bobina e uma fonte (pilha). Mostrando que quando o
capacitor está totalmente carregado, o campo elétrico é máximo. E o campo
magnético na bobina é nulo.
A figura (b) mostra que quando o capacitor
começa a descarregar surge uma corrente elétrica, o campo elétrico começa a
decrescer e o campo magnético na bobina começa a crescer. Na Figura 1 (c)
está representado quando o capacitor está totalmente descarregado, o campo
elétrico é nulo e o campo magnético na bobina é máximo (MAI, et. al., 2008).
Osciladores eletrônicos são utilizados para emitir ondas. Um oscilador
LC é formado por um indutor e um capacitor em paralelo. Seu funcionamento é
baseado na transformação de energia elétrica armazenada entre as placas do
capacitor em energia magnética da bobina. O sistema é análogo a um oscilador
massa-mola (HALLIDAY, 1984).
A característica deste tipo de circuito, conhecido como circuito LC, L
indutor e C capacitor, possui uma velocidade que flui e volta à corrente, desde
o capacitor até o indutor, e disso se produz uma frequência (f), chamada de
frequência de ressonância:
f
1
2 LC
(1)
f é medido em Hertz, C em Farad e L em Henry.
4
Ressonância elétrica
Ressonância elétrica acontece em circuitos que possuem tanto
capacitores quanto indutores. Sistemas ressonantes podem ser usados para
gerar vibrações de uma freqüência determinada, ou para obter frequências
específicas de uma vibração.
A aplicação mais evidente é na área das telecomunicações, em que as
ondas eletromagnéticas atuam como intermediárias na transmissão das
informações do transmissor até o receptor, formando o que se chama de sinal.
O Magnetron é interessante por que possui uma caixa de ressonância
análoga com as caixas de ressonância acústica presentes em instrumentos
musicais. São formadas de cavidades ressonantes. Essas cavidades
funcionam como circuitos ressonantes com baixa perda em sua frequência de
oscilação. As cavidades ressonantes de micro-ondas podem ser representadas
por um circuito LC. Para uma cavidade de micro-ondas, a energia elétrica
armazenada é igual à energia magnética armazenada na ressonância de um
circuito LC.
O fenômeno de ressonância acústica está presente nos instrumentos
musicais, o ar contido na cavidade de uma caixa de ressonância acústica
possui uma variedade de frequências de ressonância associadas aos modos
normais de vibração, constituído por uma cavidade acústica ressonante. O som
que se origina das cordas vibrantes de um instrumento musical é influenciado
pela “caixa acústica” do instrumento. Caixa de ressonância acústica
equivalente à cavidade de ressonância elétrica do magnetron do forno de
micro-ondas. (DONOSO, 2008)
Figura 02 - Caixa de ressonância acústica
Poderá ser utilizada a freqüência angular própria das oscilações não
amortecidas de um sistema massa-mola em analogia com a frequência própria
do circuito LC obtendo-se então:
5
  2v 
k
m
  2v 
1
LC

1
LC
(2)
unidades de medidas: ω = radianos por segundo, L = Henry, C = Farad.
A geração de micro-ondas é comum em dispositivos de filamento
aquecido, por que eles emitem elétrons que ao serem acelerados por um
campo elétrico tem a sua direção modificada por campos magnéticos
(CARVALHO, 2005).
De acordo com as dimensões da cavidade onde os elétrons se
propagam é obtido um circuito oscilante. Um dispositivo de filamento é o
magnetron, capaz de gerar micro-ondas (CARVALHO, 2005).
Dentro do magnetron, no seu centro existe um tubo chamado catodo
responsável por emitir elétrons acelerados, o catodo tem uma ligação com dois
filamentos que também se ligam externamente com dois terminais do
magnetron. Os elétrons acelerados são desviados por causa do campo
magnético de dois imãs permanentes e alcançam o anodo que é uma placa
contendo diversas cavidades. Cada cavidade do anodo corresponde a uma
bobina e um capacitor numa frequência de 2.450MHz (CARVALHO, 2005).
Em cada cavidade aparece um campo elétrico devido ao acúmulo de
elétrons, igual à presença de um capacitor. Os elétrons circulando em torno
das cavidades são equivalentes a um indutor. Esse dispositivo é um circuito LC
que pode ser ajustado para ser um circuito ressonante com freqüência definida.
Logo o Magnetron é análogo a um circuito LC (CARVALHO, 2005).
Figura 03 - Explicação sobre o processo fundamental de funcionamento do magnetron.
6
3.
Principio de funcionamento do Magnetron
É chamado Magnetron a válvula que produz micro-ondas na faixa de
frequência de 2.450MHz. O princípio de funcionamento do magnetron é
fundamentado no efeito de circuitos ressonantes. O circuito ressonante é capaz
de gerar ondas e é formado pela junção de uma bobina e um capacitor em
paralelo (MAI, et. al., 2008).
A Bobina é um transformador ressonante capaz de gerar uma tensão
elétrica. Quando há passagem de corrente elétrica pela bobina, um campo
magnético é gerado em torno da bobina. Se caso ocorrer o desligamento da
fonte de alimentação da bobina, que gera a corrente elétrica, esse campo
magnético diminuirá, gerando uma tensão na bobina, que manterá por um
determinado tempo a corrente ainda fluindo no mesmo sentido, preservando a
energia armazenada no circuito. Essa preservação da energia, como um
armazenamento é chamada de Indutância (MAI, et. al., 2008).
Já o capacitor, que é constituído por duas placas condutoras metálicas
separadas por algum tipo de material isolante, ocorre o armazenamento de
energia elétrica. Quando ligamos a uma fonte de alimentação, uma placa se
carregará positivamente e outra negativamente. Existirá corrente no circuito
somente durante a carga e descarga do capacitor (MAI, et. al., 2008).
Quando ligamos um conjunto bobina e capacitor em paralelo, partindo
do momento em que o capacitor está totalmente carregado, ou seja, campo
elétrico é máximo e a corrente é nula. Nesse instante os elétrons da placa
negativa do capacitor começam a fluir pela bonina para chegarem à placa
positiva do capacitor, surge uma corrente elétrica na bobina que é máxima
quando o capacitor estiver descarregado. A energia armazenada pela bobina é
em forma de energia magnética isso acontece até que as cargas do capacitor
comecem a aproximar de zero (MAI, et. al., 2008).
Como o capacitor não pode fornecer elétrons para sempre, esse fluxo de
elétrons entre placas começa a cair e conseqüentemente a corrente começa a
cair, diminuindo o campo magnético produzido na bobina. A corrente vai
diminuindo de acordo com o tempo, causando redução do campo magnético,
iniciando um fluxo de elétrons para carregar o capacitor com a polaridade
oposta à de inicio. Quando o capacitor é então carregado totalmente, a placa
negativa se transforma em positiva e a corrente nula (MAI, et. al., 2008).
7
Novamente o capacitor recebe carga através da bobina forçando uma
corrente no sentido contrário ao anteriormente descrito. O campo magnético da
bobina aumenta novamente, com sentido oposto. De acordo com que
mudamos o sentido da corrente mudamos também o sentido do campo
magnético. Então cada vez que o sentido da corrente se inverte, enquanto a
intensidade do campo magnético da bobina diminui gradativamente mantendo
o tempo suficiente até o capacitor recarregar. O ciclo é repetitivo e produz uma
corrente alternada no circuito. A carga e a descarga de um capacitor e de uma
bobina
geram
oscilações
eletromagnéticas.
Que
são
as
ondas
eletromagnéticas que emitem radiação (MAI, et. al., 2008).
O forno de micro-ondas é formado pelos componentes básicos: Porta,
painel de controle, prato giratório de vidro, suporte metálico para prato giratório,
lâmpada, dispositivo de segurança, travas de segurança, puxador e cabo de
força.
Figura 04 - Componentes básicos do forno (ELETROLUX, 2008).
8
Figura 05- Foto do forno de micro-ondas para pesquisa.
Figura 06 - Os principais componentes de um forno de micro-ondas.
Os principais componentes de um forno de micro-ondas: Magnetron, um
guia de ondas, fonte de alta tensão, transformador e um retificador, e cavidade
ou câmara de cozimento (CARVALHO, 2005).
O cozimento por micro-ondas acontece por que as micro-ondas nessa
faixa de freqüência usada nos fornos são fracamente absorvidas pelas
moléculas de água, gorduras e açúcares presentes nos alimentos. Essas
moléculas polares (que possuem pólos nos seus extremos, um positivo e outro
negativo) alinham-se com o campo elétrico da radiação e como esse campo
elétrico muda de direção de acordo com a freqüência da radiação, as
moléculas tentam acompanhar essa mudança e puxam as moléculas vizinhas.
Mas devido certa resistência da substância algumas moléculas vizinhas se
opõem ao alinhamento devido. Que gera um aquecimento do meio, ela oscila e
a radiação de micro-ondas é transformada em calor no interior do alimento
(CARVALHO, 2005).
9
A constante dielétrica da substância influencia na absorção das microondas. Ela está associada ao tempo de relaxação e o grau de polarização das
moléculas. A relaxação é o resultado dos dipolos elétricos quando submetidos
ás variações do campo elétrico que recebem (CARVALHO, 2005).
A frequência de radiação do forno de micro-ondas não é igual à
freqüência de oscilação das moléculas de água. Por que se fosse a mesma
freqüência ela seria totalmente absorvida nas primeiras camadas dos alimentos
e a parte interna não seria penetrada. A freqüência escolhida é um meio-terno
para que ocorra a penetração tanto nas primeiras camadas do alimento como
no seu interior (CARVALHO, 2005).
O campo eletromagnético alternado gerado leva a rotação e agitação
necessária que provoca colisão de moléculas polares e íons no interior dos
alimentos. Estes atritos moleculares provocados pelas colisões, que geram
calor e levam ao aumento de temperatura. Os dois mecanismos de explicação
sobre o aquecimento são a interação dipolar elétrica e iônica (FEHD, 2005).
A interação dipolar acontece quando: A molécula é um "dipolo". Parecido
com a ação do ímã, esses "dipolos" irão orientar-se quando sujeitos a campos
eletromagnéticos. As interações iônicas, compostos iônicos, sais dissolvidos na
comida também pode ser acelerado pelo campo eletromagnético e colidir com
outras moléculas para produzir calor. (FEHD, 2005).
A composição de um alimento irá influenciar a forma de como ele será
aquecido no forno micro-ondas. Alimentos com muita água serão aquecidos
mais rapidamente por causa da interação dipolar mais eficiente com a água.
(FEHD, 2005).
4.
Objetivo Específico
Estimar a freqüência de ressonância de um forno de micro-ondas.
5.
Materiais e métodos.
Através da solução do exercício 8.10 do livro Curso de Física de
Berkeley, foi possível obter uma equação para calcular aproximadamente e
estimar o valor da freqüência de um magnetron real (PURCELL, v.2, p. 401,
1973).
10
Foi feita a desmontagem de um forno de micro-ondas, os componentes
foram identificados. O magnetron foi cortado de forma que suas dimensões
pudessem ser medidas para possibilitar o cálculo da freqüência de
ressonância.
6.
Resultados
A solução de um exercício foi motivação da pesquisa sobre a válvula
magnetron.
Através
do
exercício,
obter
uma
fórmula
para
calcular
aproximadamente o valor da freqüência de ressonância de um magnetron real.
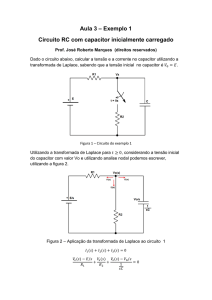
Partindo do exercício:
7.7 Calcule a auto-indutância de um solenóide cilíndrico de 10 cm de diâmetro
e 2m de comprimento. Ele tem um enrolamento de uma única camada
contendo um total de 1200 voltas (PURCELL, 1973).
L   0n 2lA
L N
m
I
(3)
, N é o número de espiras,  m é o fluxo magnético e I é a corrente.
Para um solenóide como no caso estudado faremos as seguintes
equivalências. Nesta expressão n=N/L é a densidade de espiras por unidade
de comprimento l e o fluxo magnético é  m  B  A onde B é o campo
magnético no interior do solenóide, A é a área da seção reta do solenóide.
m  B  A
(4)
B  0  n  I
(5)
onde 0 é a constante de permeabilidade do espaço livre e tem valor de
 0  4  10 7 T / m . Chegamos a conclusão que:
L N
m
I

(n  l)  ( 0  I  n  A )
  0n2lA
I
Então substituindo os valores do exercício nessa fórmula. (HALLIDAY, et. al.,
1984),. O solenóide cilíndrico de diâmetro igual a d = 10 cm, N = 1200 voltas, l
= 2 m. Fazendo as transformações necessárias.
Como r(raio) 
Diâmetro
; r  5  10 2 m
2
11
A área é A    r 2 que será  7,85  10 3 m2
L   0n 2lA
n
N 1200

 600 voltas / metro
l
2
L  ( 4  10 7 )  (600)2  (2)  (7,86  10 3  7,11 10 3
H
m
Exercício motivador da pesquisa sobre o Magnetron.
Figura 07 - Figura do exercício.
Resolução: Para escrever uma fórmula para o condutor cilíndrico de
extremos abertos, foi necessário partir do conjunto da figura (b) e deduzir que
se tratava de um indutor e um capacitor de placas paralelas.
O comportamento de um circuito LC é semelhante ao de um sistema massamola, logo fizemos as equivalências de que:
Q corresponde a x,
I corresponde a v,
C corresponde a 1 / k
L corresponde a m.
12
Se I 
dx
dQ
e v
dl
dt
Aplicando a lei das malhas de Kirchhoff ao circuito,
temos:
L
Substituindo a corrente I por
dI Q
 0
dt C
(6)
dQ
temos:
dt
d2 Q Q
L 2   0
C
dt
(7)
É semelhante que à equação de movimento massa-mola:
d2 x
m  2  kx  0
dt
Dividindo todos os termos da equação (10) por L, temos:
d2 Q
1

2
LC
dt
Que é análoga a:
d2 x
k
  x   2 x
2
m
dt
2 
(8)
k
k
onde  
que é a freqüência angular.
m
m
2
Fazendo  
1
temos:
LC

C
1
(9)
LC
0  A
d
Então no capacitor de placas paralelas temos
(10)
 0  8,85  10 12
F
pF
 8,85
m
m
F
pF que é o valor da permissividade do vácuo. A letra
 8,85
m
m
“A” representa a área, “d” é a distância entre as placas. A capacitância de um
 0  8,85  10 12
capacitor é
C
Q
V
(11)
13
Uma placa do capacitor vai ter +Q e a outra -Q. Para atraírem-se
mutuamente. Cada placa contribui para um campo elétrico entre as placas que
é E

Q
Onde   como o campo E é uniforme entre as placas, a V
0
A
diferença de potencial é igual ao produto do campo pela distância d entre as
placas. (TIPLER, 2000)
V  Ed 
C

Q d
d  
0
A 0
Q 0  A

V
d
(12)
(13)
Como o exercício é bem claro ao dizer que a freqüência de ressonância é
independe do comprimento b fazemos as substituições:
L   0n2 Al
(3)
Para a equação acima n (N/l) é a densidade de espiras, N é o número de
espiras e l é o comprimento das espiras. Para o problema é apenas 1 unidade
de espira e l é igual ao comprimento b.
1
L   0 ( )2 Al
l
L
 ( r 2 )
0 A
L 0
b
b
C

1
L C
 0  A  0  Wb

d
s

1
 0 ( r 2 )  0  Wb

b
s
O problema fala que o raio = a então obtemos a equação

1
a2
0    0  W 
s
(14)
E as medidas de s e W foram conseguidas medindo a figura (c) com um
paquímetro. Como diz o exercício a=s/2.
14
Figura 08- Largura W
Figura 09- Distância entre placas s
Medidas: s = 1,8 mm = 0,0018m W = 3,5 mm = 0,0035 m
1

( 4  10 7 )  ( )  (8,85  10 12 )  (0,0035) 
Freqüência é f 
1
2 LC
(0,5  0,0018)
(0,0018)
2
 1,348  1011
rad
s
 2,145  1010 Hz  21,454GHz  21.450MHz
Para a pesquisa experimental foi preciso encontrar a peça fundamental
da pesquisa, o magnetron, e foi necessário desmontar um forno de microondas. O forno disponibilizado foi um modelo: MS - 74MLA marca: LG
Multiondas freqüência: 2.450 MHz potência: 1.050W e rede de alimentação de:
220 v. Dimensões Gerais do Produto (L x A x P) (mm): 485x280x350; Dimensões Gerais da Cavidade (L x A x P) (mm): 308x196x316; - Capacidade:
19 litros; - Peso líquido: 12.0kg. (LG, et al, MS - 74LA)
Ao desmontar o forno de micro-ondas encontramos o magnetron e foi
possível desmontá-lo também para que fizéssemos o estudo da cavidade
ressonante, fazer os devidos cortes a cavidade para medidas necessárias ao
cálculo da freqüência de ressonância produzida e assim explicar a geração de
micro-ondas em um modelo real.
Usamos aqui uma metodologia experimental, foi feito anotações e
medidas de dados como: diâmetro da cavidade, altura e largura das placas
condutoras, medida entre placas e base das placas.
Foi fotografado o eletrodoméstico estudado, a válvula magnetron e seus
componentes. Utilizou-se o manual do próprio forno de micro-ondas para
15
nomes e medidas padrões de fábrica para as peças, a desmontagem foi toda
auxiliada pelos técnicos do laboratório.
Figura 10 - Foto do forno de micro-ondas aberto.
Figura 11 - Marca e modelo do magnetron estudado.
Magnetron LG e Modelo2M213. Através da desmontagem do forno foi
possível mostrar as principais características do magnetron real.
Figura 12 - Magnetron montado
Figura 13- Análoga ao magnetron real (PHILCO, 2008)
Essa é a estrutura do magnetron para gerar a freqüência de 2,45GHz.
16
Figura 14 - A cavidade de ressonância foi
Figura 15 - Cavidade inteira.
cortada perpendicularmente.
Mas chegamos enfim na cavidade ressonante, foi feito um corte
perpendicular e descoberto que a cavidade era formada por aletas que juntas
formavam cavidades pequenas e formato aproximado de um quadrado. A
fórmula utilizada teve de ser adaptada para a área de um quadrado. As
medidas essenciais da cavidade foram de acordo com a fórmula deduzida para
o cálculo: ela apresenta diâmetro de 40 mm. Aletas de 9,55 mm de altura e
12,80 mm de largura. A partir dessas medidas pôde ser calculada a freqüência
de oscilação das micro-ondas do magnetron real.
Essa cavidade de ressonância é composta por um ânodo, um catodo e
dois imãs fixos. O ânodo é a peça metálica que é feita com ferro ou cobre,
possui um número par de aletas formando suas cavidades. O cátodo localizado
no centro da cavidade é responsável por emitir elétrons. A antena sempre fica
ligada a uma aleta do anodo e é responsável por conduzir as micro-ondas para
a parte externa do magnetron.
A parede da cavidade ressonante funciona como uma série de bobinas e
as aletas funcionam como uma série de capacitores. Quando circula uma
corrente elétrica nesse conjunto, geram campos magnéticos e campos elétricos
variáveis nos espaços que ficam entre as aletas. Esse funcionamento é um
circuito ressonante com valores de indutância e capacitância pequenos, mas
que emitem oscilações com alta freqüência, ou seja, emite micro-ondas numa
freqüência de 2,45GHz. A antena recebe e irradia essa energia para a câmara
de cozimento através do guia de ondas. O guia de ondas é um tubo metálico
capaz de refletir e direcionar as micro-ondas.
17
Figura 16 - A cavidade com corte transversal.
7.
Figura 17 - Analogia as aletas reais.
Discussão
Utilizando a mesma questão para o cálculo experimental do magnetron
real. Foi verificado que a cavidade de ressonância é diferente da cavidade do
exercício anterior. E que a indutância e a capacitância dependem da geometria
do objeto. E que por isso os resultados serão diferentes.
Com as seguintes medidas, feitas com o paquímetro:
Figura 18 - Cavidade reta.
Figura 20 - Altura das aletas da cavidade
Figura 19 - Diâmetro da cavidade ressonante.
Figura 21 - Base da cavidade
18
Figura 22 - Distância entre placas
Figura 23 - Largura da placa
Figura 24 - Parte para subtração de valores
Obtemos: diâmetro de 40 mm, aletas de 9,55 mm de altura e 12,80 mm de
largura. Distância entre placas de 4,75 mm. Base da cavidade é 8,80 mm. A
equação para a velocidade das oscilações eletromagnéticas independe do
comprimento l da bobina, logo ao substituirmos na fórmula, ele será anulado.
L   0n2 Al
(3)
1
L   0 ( )2 Al
l
L
C

0 A
l
 0  A  0  Wl

d
s
1
LC

1
 0 A  0  Wl

l
s
Por isso a fórmula resultante é:

1
0  0  A 
W
s
(15)
19
Temos
o
valor
de
 0  4  10 7 Tm / A ,
temos
o
valor
de
 0  8,85  10 12 F / m e para o cálculo da área utilizaremos os valores medidos. A
área é aproximadamente um quadrado logo base vezes altura é a área
desejada.
  2  1010 rad/s
F

 3.183.098.862Hz  3,183GHz
2
A freqüência do magnetron real foi maior que a freqüência fixada nos
manuais dos fornos de micro-ondas. A freqüência fixada é de: 2,45 GHz. Mas é
aceitável a ordem de 2 a 3 GHz, por se tratar de um experimento, existirem
medidas aproximadas e provavelmente um percentual de erro aceitável.É
diferente do resultado do exercício do livro também por que a cavidade é
circular e do magnetron real é aproximadamente um quadrado. A geometria da
cavidade ressonante influência na freqüência emitida.
Aqui também vamos comentar as características observadas dos
principais componentes do forno de micro-ondas: Fonte de alta tensão,
transformador e um retificador, magnetron, um guia de ondas, e uma cavidade
ou câmara de cozimento.

A fonte de alta tensão é fornecida pela rede elétrica da residência;

O transformador e o retificador são para obter a alta tensão contínua
para o funcionamento da fonte de micro-ondas;

O magnetron, que produzirá um feixe intenso de micro-ondas de
freqüência definida;

Um guia de ondas, que transportará as micro-ondas até a câmara de
cozimento;

A cavidade ou a câmara de cozimento é onde as micro-ondas serão
absorvidas pelos alimentos a serem cozidos (CARVALHO, 2005).
8.
Considerações finais
A finalidade do magnetron é similar a de um oscilador elétrico e um
circuito ressonante LC. Ele foi construído para gerar micro-ondas. Freqüência
20
determinada, controlada pelo formato da cavidade ressonante. O magnetron é
o princípio fundamental de um forno de micro-ondas.
O magnetron real estudado nessa pesquisa não possui cavidades
ressonantes circulares e sim aproximadamente o formato de um quadrado.
Que foi uma surpresa para nós, ao abrirmos o magnetron e fazer o corte
perpendicular ao objeto, ver que as cavidades não eram circulares e mesmo
assim
funcionava
muito
bem
com
essa
determinada
geometria,
experimentalmente o valor foi diferente do fixado nos manuais de micro-ondas,
mas foi aproximadamente.
A proposta do exercício confrontou a teoria com a experimentação. A
teoria criou muita expectativa em dar tudo certo, valores exatos devido a
resolução do exercício de motivação. A experimentação foi mais concreta,
possibilitando abrir uma explicação sobre o funcionamento da válvula, entender
várias coisas que estavam relacionadas.
O foco principal era uma pesquisa experimental e teórica que pudesse
nos explicar o funcionamento dessa válvula, as explicações foram alcançadas,
obtivemos um trabalho com um resultado satisfatório.
9.
Agradecimentos
Deus,
“Obrigado Deus, por ter permitido que eu chegasse nesse momento tão
sublime da minha vida. Por ter sido a luz que me clareou os momentos de
escuridão e me protegeu para que nenhum mau me acontecesse até hoje.
Obrigada Deus.”
Prece de Agradecimento
10.
REFERÊNCIAS
CARVALHO, Regina Pinto de. Temas Atuais de Física: Micro-ondas.
Sociedade Brasileira de Física, 1a ed. São Paulo: Livraria da Física, 2005.
BURGOS, ELETRÔNICA NET. LTDA. Curso Prático de manutenção em forno
de micro-ondas. Disponível em
< http://www.burgoseletronica.net/apostilas/forno%20microondas.pdf > Acesso
em: 03/2011.
21
DONOSO, José Pedro. Som e Acústica: Natureza ondulatória do som. São
Paulo, 2008. Dissertação (Trabalho acadêmico em Arquitetura), Universidade
de São Paulo. Instituto de física de São Carlos - UFSC.
ELECTROLUX. Microondas. Manual de instruções: MEF33, MEG33. Curitiba,
2008.
FEHD, Departamento do Governo de Hong Kong. Serviço Alimentar e da
Saúde Pública do Ramo Alimentar e Higiene Ambiental. Disponível em
<http://www.cfs.gov.hk/english/programme/programme_rafs/programme_rafs_ft
_01_02_mcfs.html > Acesso em: 06/2005.
GRUPO DE REELABORAÇÃO DO ENSINO DE FÍSICA. Física:
Eletromagnetismo. 3a ed. São Paulo: Editora da universidade de São Paulo,
1998.
HALLIDAY, David; RESNICK, Robert. Física. 4a ed. Rio de Janeiro: LTC, v.3,
1984.
––––––. Física. 4a ed. Rio de Janeiro: LTC, v.4, 1984.
LG. Microondas: manual de instruções: MS-74MLA.
MAI, Ivo; BALZARETTI, Naira Maria; SCHMIDT, João Edgar. Textos de apoio
ao professor de física: Utilizando um forno de micro-ondas e um disco rígido de
um computador como laboratório de física. Rio Grande do Sul, 2008.
Dissertação (Mestrado Profissional em Ensino de Física), Universidade Federal
do Rio Grande do Sul.
IN INFOPÉDIA, PORTO EDITORA. Micro-ondas (física). Disponível em
< http://www.infopedia.pt/$micro-ondas-(física) > Acesso em: 22/06/2011.
ALESSANDRA, NILZA FRANCINE. Projeto Microondas. O que são microondas. Disponível em:
<http://projetomicroondas.pbworks.com/w/page/19281042/MICROONDAS >
Acesso em: 13/06/2007.
WIKIPÉDIA, A ENCICLOPÉDIA LIVRE. Oscilador LC. Disponível em:
< http://pt.wikipedia.org/wiki/Oscilador_LC > Acesso em: 03/2011
PHILCO. Microondas: manual técnico. 2008.
PURCELL, Edward Mills. Curso de Física de Berkeley: Eletricidade e
Magnetismo. São Paulo: Edgard Blücher, v.2, 1973.
TIPLER, Paul Allen. Física para cientistas e engenheiros: Eletricidade e
Magnetismo, ótica. 4a ed. Rio de Janeiro: LTC, v.2, 2000.
22