Aula 3 – Exemplo 1 Circuito RC com capacitor - metaheuro

Aula 3 – Exemplo 1
Circuito RC com capacitor inicialmente carregado
Prof. José Roberto Marques (direitos reservados)
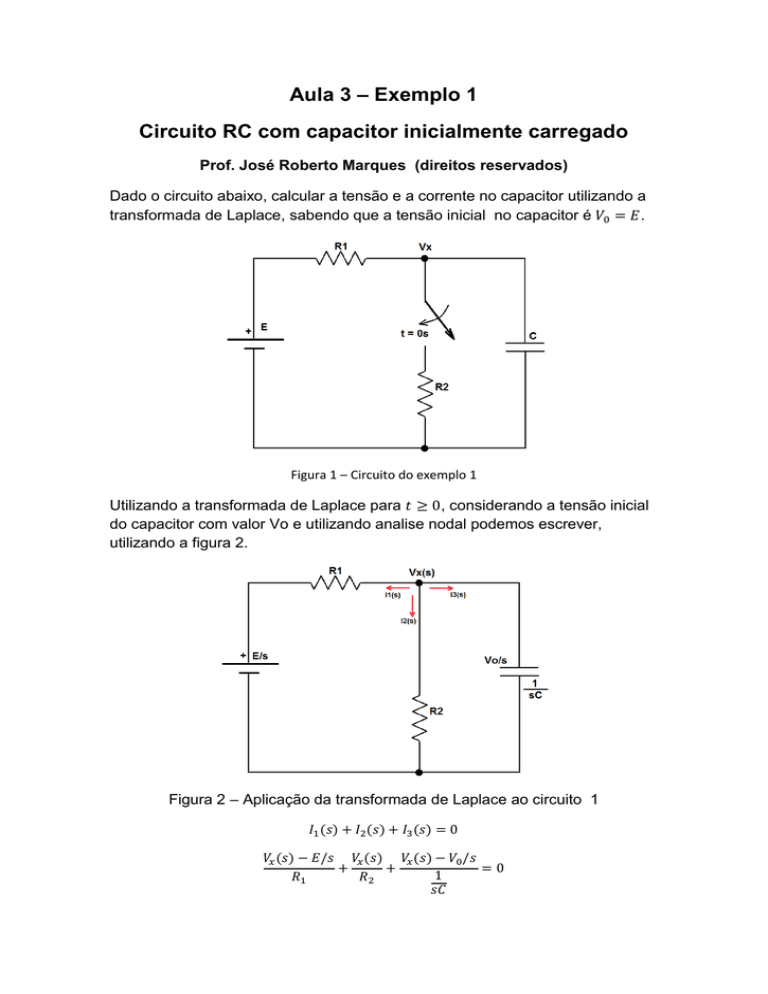
Dado o circuito abaixo, calcular a tensão e a corrente no capacitor utilizando a
transformada de Laplace, sabendo que a tensão inicial no capacitor é
.
Figura 1 – Circuito do exemplo 1
Utilizando a transformada de Laplace para
, considerando a tensão inicial
do capacitor com valor Vo e utilizando analise nodal podemos escrever,
utilizando a figura 2.
Figura 2 – Aplicação da transformada de Laplace ao circuito 1
Manipulando a expressão obtemos:
Dividindo o numerado e o denominador do primeiro membro por
Que com alguma manipulação resulta em:
Expandindo o primeiro termo do segundo membro em frações parciais
obtemos:
onde
De onde podemos escrever:
Aplicando a transformada inversa de Laplace obtemos:
.
No instante inicial (t=0) a tensão vx(t) = V0 = E, portanto:
Que colocando os termos comuns sobre o mesmo denominador dá:
Pata
.
A corrente que passa pelo capacitor é dada pela expressão
Assim
Como
temos:
A figura 3 mostra os gráficos da tensão e corrente no capacitor do exemplo
com a tensão da fonte igual a 60V, R1 = R2 = 2Ω e C=0,1F.
A figura 4 mostra as correntes em todos os componentes do circuito, lembrado
que a corrente da fonte e a mesma do resistor R1. De acordo com a lei dos nós
que nos diz que
A resolução do mesmo problema sem utilizar a transformada de Laplace.
Uma análise do circuito com a chave fechada utilizando a lei dos nós no mostra
que:
Substituindo d/dt pelo operador D obtemos:
Figura 3
Figura 4
Resolvendo a equação homogênea obtemos:
De onde podemos escrever:
Onde
e
são constantes arbitrárias.
As condições iniciais do problema nos indicam que em t = 0 a tensão no
capacitor é igual a tensão da fonte, portanto:
A corrente no capacitor é dada pela expressão:
Como, no momento do fechamento da chave o capacitor começa a
descarregar, fornecendo corrente para o resistor R2 com valor de sua tensão
dividida por R2, temos:
Como:
Portanto a tensão no capacitor é:
A corrente no capacitor é dada por:
Portanto: