Propriedades Mecânicas

Propriedades
Mecânicas
Prof. Hamilton M. Viana
Propriedades Mecânicas
Propriedades Mecânicas
)
Definem a resposta do material à aplicação de forças (solicitação
mecânica).
Força (tensão)
Î
Deformação
) Principais Propriedades:
„ Resistência
„ Fluência
„ Elasticidade
„ Dureza
„ Ductilidade
„ Tenacidade
Determinação das Propriedades Î Ensaios Mecânicos
Tipos de Solicitação
• Força lenta (estática)
• Força rápida (impacto)
• Força variável (vibração)
• Presença de trincas, entalhes ou defeitos de fabricação
• Altas temperaturas (oxidação, modificação nas propriedades)
Ensaios Mecânicos / Normas Técnicas
# Tipos de Tensões:
z Tração
z Compressão
z Cisalhamento
z Torção
# Ensaios Mecânicos:
São utilizados para determinar as Propriedades Mecânicas do
material
Utilização de corpos de prova
Utilização de Normas Técnicas
ASTM (American Society for Testing and Materials)
ABNT (Associação Brasileira de Normas Técnicas)
Propriedades Mecânicas
F
F
A0
φ
F
F
θ
F
Tração
F
F
Cisalhamento
Torção
Testes mais Comuns
# Os testes (ensaios) mais comuns utilizados
no estudo de materiais são os ensaios de:
• tração
• compressão
• torção
• choque
• desgaste
• fadiga
• dureza
Ensaio de Tração
• É o teste mais simples.
• Permite determinar diversas propriedades mecânicas importantes.
• Consiste em aplicar uma força (carga) de intensidade crescente,
tracionando o material até sua ruptura.
Corpo de prova
Máquina de ensaio (MTS)
Célula de carga e extensiômetro
Curvas:
força x alongamento
tensão x deformação
Ensaio de Tração
O que acontece com o material durante o teste de tração ?
•A
aplicação
de
uma
força (tensão) provoca a
deformação
(variação
dimensional) do material
até a sua ruptura.
Tensão (σ) x Deformação (ε)
σ = tensão (MPa, Kgf/cm2, Kgf/mm2, N/ mm2)
σ = F/A0
F = força (carga) aplicada (N ou lbf)
A0 = área da seção reta transversal (cm2, mm2)
ε = deformação
ε = (li - l0)/l0 = ∆l/l0
l0 = comprimento inicial da amostra
li = comprimento instantâneo
• A deformação não possui unidade, porem pode-se ter: m/m; cm/cm; %
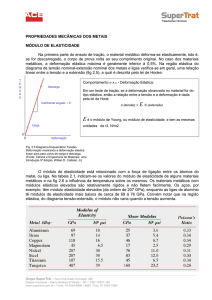
Gráfico de Tensão x Deformação
Dentro de certos limites, a deformação é proporcional à tensão (a
lei de Hooke é obedecida)
E = módulo de elasticidade (módulo de Young)
M = limite de resistência à tração
F = fratura do material
σ=Eε
Tipos de Deformação
Tensão [ σ ]
Plástica
Elástica
Deformação [ ε ]
Deformação Elástica
) Precede a deformação plástica.
)
A deformação não é permanente (reversível) Î
o material retorna à
posição inicial após retirada a força.
) A Tensão é proporcional à deformação (Lei
σ=Exε
de Hooke)
σ = tensão
E = módulo de elasticidade (módulo de Young)
ε = deformação
Deformação Elástica: Anelasticidade
)
Anelasticidade: A maioria dos metais apresenta uma “componente” de
deformação elástica dependente do tempo, ou seja, após retirada a carga é
necessário um certo tempo para que haja a recuperação do material (para o
material retornar ao seu tamanho inicial).
„ Metais: normalmente a componente
anelástica é pequena.
„ Para alguns polímeros a componente
anelástica é elevada (Comportamento
Viscoelástico)
Deformação Plástica
• Ponto “P”: até este ponto vale a Lei de Hooke
E =
σ/ε
[Kgf/mm2]
P
# Características da Deformação
Plástica:
) Está relacionado com a rigidez
do material.
)
Está relacionado diretamente com as forças das ligações inter-
atômicas, decorrente do deslocamento de átomos (ou moléculas) para
novas posições na estrutura do metal.
Módulo de Elasticidade: Exemplos
Ï o módulo de elasticidade Ð mais rígido é o material
(menor é a sua deformação elástica)
MÓDULO DE ELASTICIDADE
[E]
GPa
106 Psi
Magnésio
45
6.5
AlumÍnio
69
10
Latão
97
14
Titânio
107
15.5
Cobre
110
16
Níquel
207
30
Aço
207
30
Tungstênio
407
59
* 1 psi = 6,90 x 10-3 MPa = 7,03 x 10-4 kg/mm2
• O comportamento elástico
também é observado quando
forças compressivas, tensões
de cisalhamento ou de torção
são aplicadas ao material
Limite de Elasticidade
)
Ponto “P”: Corresponde à máxima tensão
que o material suporta sem sofrer deformação
permanente.
P
Deformação Elástica: Coeficiente de Poisson
) Quando o material é submetido a uma tensão de tração (ou compressão),
ocorre um “ajuste” (acomodação) nas dimensões perpendiculares à direção
da força aplicada.
)
O Coeficiente de Poisson (ν) é definido como a razão (negativa) entre
as deformações lateral (εx,
εy) e longitudinal (ou axial, εz) do material.
Teremos εx = εy quando o material é isotrópico e a
tensão aplicada for uniaxial (apenas na direção “z”)
)
Deformação Elástica: Coeficiente de Poisson
„ Teoricamente, materiais isotrópicos devem apresentar um coeficiente
de Poisson de 0.25.
„ O máximo valor para “ν” é 0.5 (valor para o qual não existe qualquer
alteração líquida no volume)
„ Para muito metais e ligas, este valor está entre 0.25 e 0.35
„ O coef. de Poisson também é usado na relação entre os módulos de
cisalhamento ( G ) e e de elasticidade ( E ) de materiais “isotrópicos”,
pela relação:
E = 2G (1 + ν)
Para a maioria dos metais G ≈ 0,4E
Coef. de Poisson x Tensão de Cisalhamento
• Tensão de Cisalhamento ( τ ) é a relação entre a força aplicada e a
área submetida ao cisalhamento:
F = força (ou carga) paralela ás faces superior
e inferior do corpo de prova.
τ = F / A0
A0 = área da das faces superior e inferior.
• Tensões de cisalhamento produzem deslocamento de um plano de átomos
em relação ao plano adjacente
• A deformação elástica de cisalhamento ( γ ) é dada por:
γ = tgα
α
τ = Gγ
G = módulo de cisalhamento (ou módulo transversal)
γ = deformação de cisalhamento (está relacionada ao
ângulo de torção)
Deformação Plástica: Escoamento
) Esse fenômeno é nitidamente observado em alguns metais de natureza
dúctil, como aços com baixo teor de carbono.
) Caracteriza-se por um grande alongamento sem acréscimo de carga.
) Para a maioria dos materiais metálicos, a deformação elástica persiste
apenas até deformações de ≈ 0,005. Após este ponto ocorre a
deformação plástica (não-reversível).
A lei de Hooke não é mais válida !
Em nível atômico, a deformação Plástica é causada pelo “deslizamento”,
onde ligações atômicas são quebradas pelo movimento de deslocamento, e
novas ligações são formadas.
Deformação Plástica
σy = tensão de escoamento (dá a capacidade de um material resistir à deformação
plástica)
• Curva “a”: a transição do comportamento elástico para o plástico é gradual, iniciando
uma curvatura a partir do ponto “P”.
• Curva “b”: em alguns aços (e
outros
materiais)
o
limite
de
escoamento é bem definido, ou
seja, o material escoa deformandose plasticamente sem aumento da
tensão.
Deformação Plástica: Limite de Escoamento
„ O ponto de escoamento pode ser determinado como sendo o ponto onde
ocorre o afastamento inicial da linearidade na curva tensão-deformação.
Convenção: o limite de escoamento
corresponde à tensão necessária
para promover uma deformação
permanente de 0,2% (denominada
de “tensão limite de escoamento” -
σe
σe ). O valor de σe corresponde à
interseção entre uma linha reta,
construída
paralela
a
porção
elástica, e a curva de tensão x
deformação.
0,002
Limite de “Resistência à Tração”
„ O “Limite de Resistência à Tração” - LRT, corresponde à tensão
máxima (ponto M) aplicada ao material antes da ruptura. (se esta tensão
for mantida ocorrerá a fratura do material)
„ É calculada dividindo-se a carga (força) máxima suportada pelo
material pela área de seção reta inicial
LRT
)
Unidades: MPa; psi
1 MPa = 145 psi
1 psi = 7,03 x 10-4 kgf/mm2
M
Ductibilidade
Def.: Representa uma medida do grau de deformação plástica que o
material suportou quando de sua fratura, ou seja, corresponde à
elongação total do material devido à deformação plástica.
Pode ser expressa como:
)
Alongamento Percentual:
AL% = (lf - l0/l0) x 100
Onde l0 e lf correspondem, respectivamente,
aos comprimentos inicial e final (após a
ruptura) do material.
) Redução de Área Superficial:
RA% = (A0 - Af/A0) x 100
Onde A0 e Af correspondem,
respectivamente, as áreas da
seção reta inicial e final (após a
fratura) do material.
Dúctil x Frágil
Materiais
frágeis:
são
considerados,
de
maneira aproximada, como sendo aqueles que
possuem uma deformação de fratura que é
inferior a ≈ 5%.
Resiliência
Def.: É a capacidade de um material absorver energia quando este é
deformado elasticamente e depois, com o descarregamento, ter essa
energia recuperada.
) A propriedade associada é dada pelo módulo
Ur = 1/2 (σe x εe) = (σe)2/2E
)
de resiliência (Ur)
σe
A área sob a curva, que representa a
absorção de energia por unidade de volume,
corresponde ao módulo de Resiliência Ur.
εe
) Materiais resilientes são aqueles que têm alto limite de elasticidade e
baixo módulo de elasticidade (como os materiais utilizados para molas).
Tenacidade
Def.: Corresponde à capacidade do material de absorver energia até sua
ruptura.
Unidade Î [Energia/volume]
Depende: da geometria do corpo de
prova e da maneira como a carga
(força) é aplicada.
• Para pequenas taxas de deformação, a tenacidade é determinada pela
área da curva de tensão-deformação (teste de tração)
• A tenacidade à fratura é uma propriedade indicativa da resistência do
material à fratura quando este possui uma trinca.
Tensão e Deformação Verdadeiras
• No cálculo da tensão de deformação (σ = F/A0) não é levado em
consideração a variação da área da seção reta (A0).
TENSÃO VERDADEIRA:
σv = F/Ai
DEFORMAÇÃO VEDADEIRA:
ε v = ln (li/l0)
Onde:
Ai = é a área da seção transversal instantânea (m2)
li = comprimento instantâneo
l0 = comprimento inicial
*Se não há variação de volume Î Ai.li = A0.l0
*ε v = ln (Ai/A0)
Tensão e Deformação Verdadeiras
RELAÇÃO ENTRE TENSÃO VERDADEIRA E CONVENCIONAL:
σv = σ (1+ ε)
RELAÇÃO ENTRE DEFORMAÇÃO VERDADEIRA E CONVENCIONAL:
ε v = ln (1+ ε)
)
As equações acima são válidas apenas para situações até a
formação do pescoço. A partir deste ponto, a tensão e deformação
verdadeiras devem ser computadas partir de medições de carga
(força), da área da seção reta e do comprimento útil reais.
Tensão e Deformação Verdadeiras
• Durante a formação do pescoço existe um estado de “tensão complexo”
na região do pescoço, devido a existência de componentes de tensão além
da tensão axial.
• Deste modo a curva de tensão correta (axial) x deformação deve ser
corrigida pela expressão:
σv =
k.εvn
K e n são constantes que dependem
do material e do tratamento (térmico
ou por encruamento) dado ao
material.
correta
Propriedades Mecânicas x Temperatura
# A temperatura é uma variável que influencia as propriedades
mecânicas dos materiais.
O aumento da temperatura provoca:
Ð Módulo de Elasticidade
Ð Força de
Ï ductibilidade
Resumo
Exemplo 1
• Um pedaço de cobre originalmente com 305 mm de comprimento é puxado em
tração com uma tensão de 276 MPa. Se a sua deformação é inteiramente elástica, qual
será o alongamento resultante ?
σ = E.ε
∆l =
ε = ∆l / l0
Tabela: E = 110 x 103 MPa
σ.l0 / E = (276 x 305) / (110 x 103)
∆l = 0,77 mm
Exemplo 2
• Uma tensão de tração deve ser aplicada ao longo do eixo referente ao comprimento de
um bastão cilíndrico de latão, que possui um diâmetro de 10 mm. Determine a
magnitude da carga exigida para produzir uma alteração de 2,5 x 10-3 mm no diâmetro.
A deformação é puramente elástica
d0
Dados:
di
d = 10 mm = 10-2 m
∆d = 2,5 x 10-3 mm
z
εz = ∆l / l0 = (li - l0) / l0
εx = ∆d / d0 = (di - d0) / d0
li
l0
x
Exemplo 2: cont.
εx
= ∆d / d0 = (- 2,5 x 10-3) / 10 =
- 2,5 x 10-4
εz = - εx / ν = - (- 2,5 x 10-4) / 0,34 = 7,35 x 10-4
σ = εz.E = (7,35 x 10-4) . (97 x 109) = 71,3 MPa
F = σ.A0
O sinal “-” deve-se à redução
no diâmetro do material
Para o latão ν = 0,34 (tabela)
Para o latão
(tabela)
= σ. (d0/2)2.π = (71,3 x 106) x (10-2 / 2)2. π
F = 5600 N
E = 97 GPa