EXERCÍCIOS EM AULA (AULA 01) - Funções I: Exercício 1: Quais

EXERCÍCIOS EM AULA (AULA 01) - Funções I:
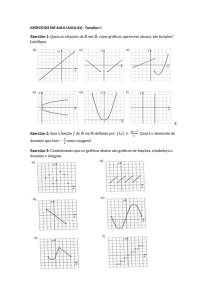
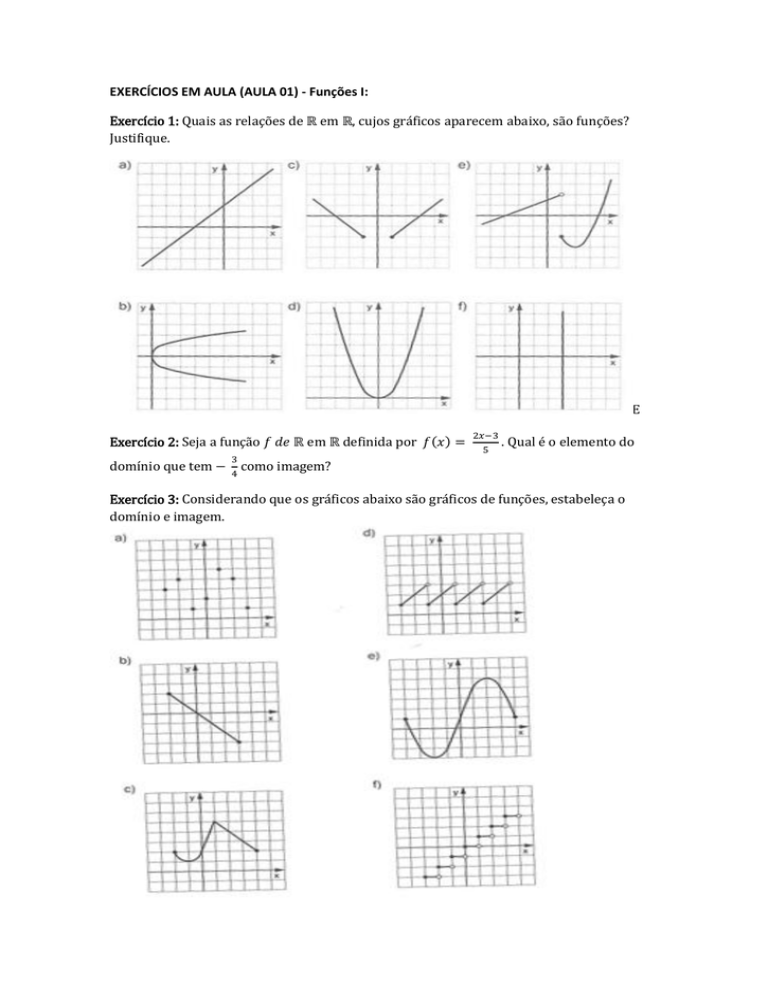
Exercício 1: Quais as relações de ℝ em ℝ, cujos gráficos aparecem abaixo, são funções?
Justifique.
E
Exercício 2: Seja a função
domínio que tem
ℝ em ℝ definida por
. Qual é o elemento do
como imagem?
Exercício 3: Considerando que os gráficos abaixo são gráficos de funções, estabeleça o
domínio e imagem.
Exercício 4: Dê o domínio das seguintes funções reais:
a)
b)
c)
d)
e)
f)
g)
h) t(x) =
i) u(x) =
Exercício 5: Sendo x
, determine o conjunto imagem da função
Exercício 6: As funções de ℝ em ℝ, definida por f(x)=
g(x)=x, são iguais? Justifique.
,
+
.
ℝ em ℝ, definida por
Exercício 7: (UNESP-SP) Numa fazenda, havia 20% de área de floresta. Para aumentar essa
área, o dono da fazenda decidiu iniciar um processo de reflorestamento. No planejamento
do reflorestamento, foi elaborado um gráfico fornecendo a previsão da porcentagem de
área de floresta na fazenda a cada ano, num período de 10 anos. Esse gráfico foi modelado
pela função f(x) =
, que fornece a porcentagem de área de floresta na fazenda a cada
ano x, onde a, b e c são constantes reais. Com base no gráfico, determine as constantes a, b
e c e reescreva a função f(x) com as constantes determinadas.
Exercício 8: Construa o gráfico cartesiano das seguintes funções de ℝ em ℝ:
a) y = 3x+2;
b) y =
;
c) y = 2x+3;
d) y =
Exercício 9: Obtenha a equação da reta que passa pelos pontos:
;
a) (2, 3) e (3, 5);
b) (1, -1) e (-1, 2);
c) (3, -2) e (2, -3);
d) (1, 2) e (2, 2).
Exercício 10: Paulo e Joana recebem o mesmo salário por hora de trabalho. Após Paulo ter
trabalhado 4 horas e Joana 3 horas e 20 minutos, Paulo tinha a receber R$ 45,00 a mais
que Joana. Calcule em reais um décimo do que Paulo recebeu.
Exercício 11: Construa os gráficos das seguintes funções definidas em ℝ
a) y = x²;
b) y = 2x²;
c) y = x²
Exercício 12: Determine os valores de m para que a função quadrática
tenha dois zeros reais e distintos.
Exercício 13: Dadas as equações
e
, sabe-se que uma
das raízes da segunda equação é o dobro de uma das raízes da primeira equação. Sendo
k
, determine k.
Exercício 14: Determine os vértices das parábolas (a)
e (b)
Exercício 15: Uma parede de tijolos será usada como um dos lados de um curral
retangular. Para os outros lados iremos usar 400 metros de tela de arame, de modo a
produzir área máxima. Qual o quociente de um lado pelo outro?
Exercício 16: Construa o gráfico cartesiano das seguintes funções definidas em ℝ e estude
seus sinais:
a)
b)
Exercícios de fixação AULA 01 (para casa):
Exercício 17: Seja
de ℝ em ℝ assim definida por f(x)=
a)f(3)
c)f
e)f
b)f
d)f(
f) f(0,75)
Exercício 18: Seja a função
ℝ
em ℝ definida por
. Calcule:
. Qual é o elemento
do domínio que tem imagem 2?
Exercício 19: Sejam as funções ,
de ℝ em ℝ, de inidas por
Quais delas são iguais entre si?
Exercício 20: As funções f: ℝ
=
, são iguais? Justifique.
ℝ, dada por f(x)= x + 1, e g: ℝ
,
,
ℝ, dada por g(x)
Exercício 21: (UFMG) Neste plano cartesiano, estão representados os gráficos das funções
y=f(x) e y=g(x), ambas definidas no intervalo aberto ,
Seja S ⊂ ℝ o conjunto definido por S = {x
ℝ f x
g x
Exercício 22: (PUC-MG) A função f é tal que f(x)=
parábola abaixo, então qual o domínio de f ?
Encontre S.
Se o gráfico da função g é a
Exercício 23: Resolva analítica e graficamente os sistemas de equações abaixo:
a)
b)
c)
Exercício 24: De uma caixa contendo bolas brancas e pretas, retiraram-se 15 brancas,
ficando a relação de 1 branca para 2 pretas. Em seguida, retiraram-se 10 pretas, restando,
na caixa, bolas na razão de 4 brancas para 3 pretas. Determine quantas bolas havia,
inicialmente, na caixa.
Exercício 25: Dados os gráficos das funções de ℝ em ℝ, obtenha a lei de correspondência
dessas funções.
Exercício 26: Determine os zeros reais das funções abaixo:
a) f(x) =
;
b) f(x) =
;
c) f(x) =
Exercício 27: É dada uma folha de cartolina como na figura abaixo. Cortando a folha na
linha pontilhada resultará um retângulo. Determine esse retângulo, sabendo que a área é
máxima.
Exercício 28: Determine a imagem das seguintes funções definidas em ℝ
a)
b)
EXERCÍCIOS EM AULA (AULA 02) - Funções II:
Exercício 1: Estude o sinal das funções cujos gráficos estão representados abaixo:
Exercício 2: Estude os sinais das seguintes funções definidas em ℝ
a) y = 2x+3;
b) y =
;
c) y = 2x
;
Exercício 3: Para que valores do domínio da função de ℝ em ℝ definida por
a
Imagem é menor que 4.
Exercício 4: Sejam as funções
Para que valores de x
a)
,
definidas em ℝ.
ℝ, tem-se:
b)
c)
Exercício 5: Resolva, em ℝ, as inequações abaixo:
a)
;
b)
;
c)
;
d) (3x 2)²
(3x 1)²>(x+2)²
g)
(x 1)²;
e)
h)
j)
;
m)
;
;
;
l)
;
o)
Exercício 6: Ache os valores reais de x para os quais vale a desigualdade
Exercício 7: Resolva as inequações abaixo em ℝ:
a)
b) –
c) –
d) –
Exercício 8: Resolva a inequação (
Exercício 9: Dentre os números inteiros que são soluções da inequação
(
, qual é o maior?
Exercício 10: Determine, em ℝ, o conjun o solução das ine uações
a
x
;
b)
c)
Exercício 11: Ache o domínio da função
em ℝ
Exercício 12: Resolva os sistemas de inequações abaixo:
a)
b)
;
i)
k)
n)
f)
;
.
Gabarito Aula 1:
1. a, d, e são funções.
2. x=-3/8.
3. Domínios: a) {-3,-2,-1,0,1,2,3}, b) [-2,3], c) [-2,4], d) [-3,5[, e) [-4,4], f) [-4,4[.
Imagens: a) {1,2,3,4,5}, b) [-3,2], c) [1,5], d) [1,3[, e) [-3,5], f) [-3,3].
4. a) ℝ, b) ℝ
, c) ℝ
g) ℝ, h) ℝ
, i) ℝ
, , d) [1, +∞ , e) ]-1, +∞ , f)
.
5. y ℝ y
6. Não são iguais, pois para x < 0 temos
x
7. a=100, b=1, e c=10; f(x)=
8.
9. a) y = 2x – 1; b) y =
10. R$ 27,00
11.
; c) y = x – 5; d) y = 2.
ℝx
ex
,
12. m >
em
13. k = 6.
14. a) V(0,-4).
16. a)
b) V( , ).
;
.
b)
15. 2.
.
,
ℝ.
Gráficos:
17. a)1, b) 1, c) 1 +
, d) 1, e)
, f) 1.
18. x = -4.
19. Todas são iguais, pois são todas funções de ℝ em ℝ e associam cada número real ao
seu cubo.
20. Não são iguais, pois não têm o mesmo domínio.
21. { x
ℝ
22. { x
ℝ
x
x
ℝ
23. a) Par ordenado (-1,2). b) S = {(-2,4)}. c) S = {(2-1)}.
Resolução gráfica do item a):
24. 23 brancas; 16 pretas.
25. a) y =
26. a) x =
; b)
-
ou x = 2.
b) x = -1 ou x =
27. O retângulo de lados 4 cm e 3 cm.
y ℝ y
}.
Gabarito Aula 2:
1. a f x
⇔x
-5 ou x = 2 ou x = 6.
f x
⇔x
f x
⇔ -5 < x < -3 ou 2 < x < 6.
b g x
⇔x
-5 ou -3 < x < 2 ou x > 6.
-3 ou x = -1 ou x = 3.
g x
⇔ -3 < x < -1
g x
⇔x
-3 ou x > - e x
c h x
⇔x
-2.
h x
⇔x
-2.
.
c) x =
28. a Im
ou x = y
ℝ y
.
- }.
b) Im
2.
3. x<3
4. a x
; b) x >
c
x ℝ
5.
a S
x ℝ x
h S
x ℝ ∅
b S
x ℝ x
i S
x ℝ| x > 1}.
c S
x ℝ| x > -3}.
j S
x
d S
x ℝ| x < 0}.
x ℝ| x >
x ℝ|
6. S
x ℝ x
x
.
n S
ℝ| x <
ou
o S
ou x
d) S = ∅.
x
x
ℝ|
<x<
y
b S
x ℝ|
}.
ou
ℝ x
ou
}.
x
ou x > 5}.
ou x > 4}.
7. a) S = x ℝ| x < 1 ou x > 2 }.
c) S =
x
x > 2}.
l S
g S
ℝ| x < -1 ou x
ℝ x<
}.
x
k S
}.
x
<x<
> }.
e) S = x ℝ| x > 1}.
f S
m S
ℝ|
x
8. S
10. a
x ℝ| -1 < x < 1 ou 2 < x < 3 }.
x ℝ|
11.
12. a S
b
x ℝ|
}.
x ℝ|
x ℝ|
9. 19.
}
}
b) S =
c)
ℝ|
}
EXERCÍCIOS EM AULA (AULA 03) - Funções
III:
Exercício 1: Encontrar todos os números x
tais que
h) 1 +
i)
x
j)
x
x
=x
x
+
−
x
=
x
=1
a) |x − 3| = 8
b) |x − 1| · |x + 1| = 0
Exercício 3: Encontrar todos os números x
tais que:
c) |x − 1| · |x + 2| = 3
a) |x − 3| < 8
Exercício 2: Resolva as seguintes
igualdades:
b) |x + 4| < 2
c) |x − 1| + |x − 2| > 1
a) |x| = −x + 2
d) |x − 1| + |x + 1| < 2
b) |−x + 2| = 2x + 1
e) |x − 1| + |x + 1| < 1
c) |x + 1| + |x − 2| = 1
d) | 5x −
− 6| =
− 5x + 6
e) |x − 1| − 2 |x − 2| + 3 |x − 3| = 4
f) |
g) x
− 2| + 2x + 1 ≥ 0
=8−
x
Exercício 4: Resolva as seguintes
desigualdades:
a) |x − 2| − |x + 2| > 2
b)
c)
x−
x>1
x -
x >0
Gabarito
h) S = {5/2 + (
Exercício 1:
i) S = {43/22 + (3
a) S = { -5, 11}
j) S = {109}
b) S = {-1, 1}
Exercício 3:
c) S = { 1/2(-1 -
), 1/2(
– 1) }
/ 2)}
)/22}
a) S =
b) S =
Exercício 2:
b) S =
a) S = {1}
d) S =
b) S = {1/3}
e) S =
c) S =
d) S =
Exercício 4:
e) S =
a) S =
f) S =
–
b)
g) S = {8}
c)
–