MATEMÁTICA 3

MATEMÁTICA 3
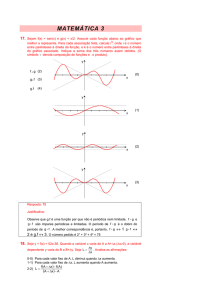
17. Sejam f(x) = sen(x) e g(x) = x/2. Associe cada função abaixo ao gráfico que
k
melhor a representa. Para cada associação feita, calcule i , onde i é o número
entre parênteses à direita da função, e k é o número entre parênteses à direita
do gráfico associado. Indique a soma dos três números assim obtidos. (O
símbolo denota composição de funções e . o produto).
y
f g (2)
(0)
x
g f (3)
g.f
(4)
y
(1)
x
y
(2)
x
y
(3)
x
Resposta: 75
Justificativa:
Observe que g.f é uma função par que não é periódica nem limitada. f g e
g f são ímpares periódicas e limitadas. O período de f g é o dobro do
período de g f . A melhor correspondência é, portanto, f g
↔1 g f ↔
2 e g.f ↔ 3. O número pedido é 2 + 3 + 4 = 75
1
2
3
18. Seja y = f(x) = 52x-36. Quando a variável x varia de A a A+∆x (∆x≠0), a variável
dependente y varia de B a B+∆y. Seja L =
∆y
. Analise as afirmações:
∆x
0-0) Para cada valor fixo de A, L diminui quando ∆x aumenta.
1-1) Para cada valor fixo de ∆x, L aumenta quando A aumenta.
f (A + ∆x ) − f ( A )
2-2) L =
(A + ∆x ) − A
3-3) L é a tangente do ângulo que o gráfico de f faz com o eixo das abcissas.
4-4) Quando A = 0, L = - 36.
Resposta: FFVVF
Justificativa:
∆y = f(A +∆x) – f(A) = 52 (A+∆x) – 36 – (52A - 36) = 52∆x. Assim, L é
constante e igual a 52, logo 0-0, 1-1 e 4-4 são falsas. 2-2 segue de ∆y = f(A
+∆x) – f(A). 3-3 é verdadeira, pois L é o coeficiente angular da reta y = 52x36
19. A cada uma das seis igualdades abaixo está associado um número, que
aparece entre parênteses abaixo do sinal de igualdade. Indique a soma dos
números correspondentes às igualdades que se verificam para quaisquer
números reais positivos x e y. Caso nenhuma igualdade se verifique, indique
00.
ln(x) = ln(x) + ln(1) = ln(x+1) = ln
( 2)
(3 )
( 4)
yx 3 + 1
=
yx 2 + 1 ( 20 )
ln(yx3+1) – ln( yx2+1) = ln(yx3) - ln(yx2) = ln(x)
(30 )
( 40 )
Resposta: 62
Justificativa:
ln (1) = 0, logo, 2 se verifica, e 3 não. 4 não se verifica para y = 1 = x. 20 se
verifica, pois ln (a/b) = ln (a) – ln (b) para quaisquer a e b positivos. 30 não
se verifica para y = 1 e x = 2, pois, neste caso, o lado esquerdo é ln (9/5), e o
lado direito é ln (2). 40 se verifica, pois ln (yx3) - ln (yx2) = ln (y) + 3ln(x) – (ln
(y) + 2ln(x)) = ln (x).
20. Seja n1 o número de raízes da função sen( x ) no intervalo [0, 10], e seja n2 o
2
número de raízes da função sen(x ) no intervalo [0,10]. Indique n1+n2.
Dado: (3,1)π<π <10<(3,2)π<4π
Resposta: 34
2
2
Justificativa:
π 2<10<4π 2
π < 10 < 2 π , logo n1 = 2.
(3,1)π < 10 < (3,2)π
2
31π <10 <32π, logo n2 = 32
21. O conjunto dos números reais x tais que 4 ≤ |x-8| ≤ 20 é formado por dois
intervalos. Indique a soma dos comprimentos destes.
Resposta: 32
Justificativa:
Se x ≥ 8 a desigualdade dada torna-se 4 ≤ x-8 ≤ 20 ou 12 ≤ x ≤ 28; se x ≤ 8
temos 4 ≤ 8-x ≤ 20 ou -12 ≤ x ≤ 4. Logo, o conjunto em questão é [12, 28] U
[-12, 4]
22. Seja K um número natural da forma K=(n+1)(n+2)(n+3)(n+4), onde n é um
número natural. Analise as afirmações:
0-0) K é par, para todo natural n.
1-1) K é múltiplo de 3, para todo natural n.
2-2) K é múltiplo de 4, para todo natural n.
3-3) K é múltiplo de 9, para todo natural n.
4-4) 4! divide K, para todo natural n.
Resposta: VVVFV
Justificativa:
Dentre 4 números naturais consecutivos, um deles é par e outro, é múltiplo
de 4; e um deles é múltiplo de 3; logo 0-0, 1-1, 2-2 e 4-4 são verdadeiras.
Para n=1, 3-3 é falsa.
23. Seja ABCDEF um hexágono regular situado em um plano com um sistema de
coordenadas cartesianas de maneira que A = (4, 2) e B = (10, 2). O hexágono
encontra-se no primeiro quadrante do sistema de coordenadas. Considerando
estes dados, analise as afirmações a seguir.
0-0) C = (3, 2 + 3 3 )
1-1) O hexágono tem lado medindo 6.
2-2) A circunferência inscrita no hexágono tem centro no ponto (7, 2+3 3 ).
3-3) A circunferência circunscrita no hexágono tem equação
(x – 7)2 + (y – 2 - 3 3 )2 = 62.
3 (x – 2).
4-4) A diagonal AD está contida na reta y – 4 =
Resposta: FVVVF
Justificativa:
O lado BC, que mede o mesmo que AB = 6, forma com a reta passando por
A e B um ângulo de 60o; portanto, a abscissa de C é 10 + 6cos 60o = 13 e a
ordenada é 2 + 6sen 60o = 2 +3 3 . Segue que 0-0 é falsa e 1-1 é
verdadeira. A circunferência inscrita no hexágono tem centro no ponto de
interseção G, entre as diagonais AD e BE; logo ABG é eqüilátero e G = (7,
2+3 3 ), portanto, 2-2 é verdadeira. A circunferência circunscrita ao
hexágono tem centro em G e raio 6, logo sua equação é (x – 7)2 + (y – 2 3 3 )2 = 62, e 3-3 é verdadeira. A reta contendo a diagonal AD tem
inclinação tg 600 =
=
3 e passa pelo ponto A = (4,2); logo tem equação y – 2
3 (x – 4) e 4-4 é falsa.
24. Considerando as funções f1, f2 , f3 : IR - {0, 1} → IR - {0, 1}, com IR sendo o
conjunto dos números reais e f1(x) = x, f2(x) = (x – 1)/x e f3(x) = 1/(1 – x) ,
analise as afirmações a seguir. A composição de funções será denotada por .
0-0) f1, f2 e f3 são funções bijetoras.
1-1) f2 é a função inversa de f3.
2-2) f2 f2 = f3
3-3) f3 f3 = f2
4-4) f3 f3 f3 = f1
Resposta: VVVVV
Justificativa:
f1, f2 , f3 têm inversas f1, f3, f2 respectivamente, daí 0-0 e 1-1 são verdadeiras.
f2 f2(x) = f2(f2(x)) = [(x - 1)/x – 1]/[(x – 1)/x] = 1/(1 – x) =f3(x). Segue que f3 f3
= f2 e, portanto, 2-2 e 3-3 são verdadeiras. f3 f3 f3 = f2 f3 = f1 e 4-4 é
verdadeira.
25. Considerando as matrizes
1 0 − 1 0
0
1
A=
, B = e I = ,
−1 −1
1 0
0 1
analise as afirmações seguintes:
4
0-0) A = I
3
1-1) B = I
1 1
2-2) AB =
0 1
12
3-3) (AB) = I
4-4) AB = BA
Resposta: VVVFF
Justificativa:
Temos A 2 =
Temos B 2 =
−1 0
e A4 = I, logo 0-0 é verdadeira.
0 −1
−1 −1
1
1
e B3 = I, logo 1-1 é verdadeira. Temos AB = e
1 0
0 1
1 0
e BA ≠ AB e 4-4 é falsa.
portanto 2-2 é verdadeira. Entretanto, BA =
−1 1
1 2
1 3
1
, ( AB)3 =
, ( AB)4 =
( AB)2 =
Temos
0 1
0 1
4
1 n
,
,...,( AB)n =
0 1
0 1
portanto, 3-3 é falsa.
26. Uma estrada retilínea deve ser construída entre os pontos A e B. Uma elevação
na direção conectando estes pontos força a construção de um túnel entre os
pontos C e D. Para descobrir os pontos C e D dos extremos do túnel, utilizamos
um ponto E, tal que são conhecidos a distância entre E e A, a distância entre E
e B e o ângulo AEB. Sabendo que AE=10(1+ 3 ) km, BE=20 km e que o
ângulo AEB mede 60o, indique a medida, em graus, do ângulo EAB.
E
C
A
B
D
Resposta: 45
Justificativa:
Usando
a
lei
dos
2.10(1+
3 ).20.1/2
cosenos
temos
AB2
=
100(4+2
3 )+400-
= 100.6 e AB = 10 6 . Usando a lei dos senos
20/sen(EAB) = 10 6 /sen(60o) e segue que sen(EAB) = 2.(
3 /2)/
6 =
o
2 / 2 e EAB mede 45 .
27. O polinômio p(x) = x2 + ax + b, com a e b números reais, divide os polinômios
f(x) = x4 + 2x3 + x2 – 9 e g(x) = x3 - 2x2 - 9. Determine a e b e indique p(7).
Resposta: 59
Justificativa:
Dividindo f(x) por g(x) obtemos quociente x + 4 e resto 9x2 + 9x +27 = 9(x2 +
x + 3). Então p(x) divide 9(x2 + x + 3) e tem coeficiente líder 1, logo p(x) =
x2 + x + 3 e p(7) = 59.
28. Efetuadas n medidas de certos objetos foram obtidos os resultados abaixo para
o percentual de objetos correspondendo a cada uma das medidas.
Medida
Percentual
12,4cm
12,25%
12,6cm
25%
12,8cm
50%
13,0cm
12,75%
Se os resultados para os percentuais são exatos, determine o menor valor
possível para n e indique n/10.
Resposta: 40
Justificativa:
Temos 12,25/100 = 1225/10000 = 49/400 e 12,75/100 = 1275/10000 =
51/400. O número n de medidas é divisível por 400, seu menor valor é 400 e
n/10 = 40.
29. A ilustração abaixo representa parte do gráfico de uma função
f(x) = a + b.cos (πx/c) com período 8, sendo a, b e c números reais. O gráfico da
função passa pelos pontos (0,12) e (4,2). Calcule a, b e c e indique abc/10.
y
12
10
8
6
4
2
0
1 2
3 4 5 6
7
8
x
Resposta: 14
Justificativa:
Como a função tem período 8, temos 2π/(π/c) = 8 e c = 4. De f(0) = 12 segue
que a + b = 12; de f(4) = 8 segue que a + bcos π = 2 ou a – b = 2.
Resolvendo o sistema, obtemos a = 7 e b = 5.
30. A hipérbole de equação x2 - y2 + 2y = 0 e a circunferência de equação x2 + y2 =
4 se interceptam em três pontos não colineares. Determine a área A do
triângulo com vértices nestes três pontos e indique A2.
Resposta: 27
Justificativa:
Subtraindo as equações das cônicas, obtemos 2y 2 – 2y = 4 que eqüivale a y
2
– y –2 = 0 que tem soluções y = 2 e y = -1. Para y = 2 temos x = 0 e
para y = -1 temos x = ± 3 . Os vértices do triângulo são (0,2) e ( ± 3 ,-1).
O triângulo tem base 2 3 e altura correspondente 3; logo, A = 2 3 .3/2 =
3 3 e A2 = 27.
31. Um depósito de cereais é composto de um cilindro circular reto de raio da base
medindo 4m e altura 6m e de um tronco de cone com raios das bases medindo
4m e 1m e altura 1,5m, como ilustrado na figura abaixo.
6m
1,5m
Calcule o volume do depósito, em m 3, aproxime para o inteiro mais próximo e
indique a soma dos seus dígitos. Dado: use a aproximação π ≅ 3,14.
Resposta: 10
Justificativa:
Seja h a altura do cone retirado para obtermos o tronco. Temos 4/(1,5+h) = 1/h
2
2
2
e daí h = 1,5/3 = 0,5m. O volume do depósito é π4 .6 + π(4 .2 - 1 .0,5)/3 =
3
334,41m .
32. O segredo de um cofre é formado de uma seqüência de quatro dígitos distintos.
Se o quarto dígito é o dobro do primeiro, determine o número N de possíveis
segredos. Indique a soma dos dígitos de N.
Resposta: 08
Justificativa:
O segredo é um número da forma 1_ _ 2, 2_ _ 4, 3 _ _6, 4 _ _8 e o número
de formas de escolher os dois dígitos do meio é 4. 8.7 = 224.