Conjuntos Enumeráveis e N˜ao-enumeráveis Para quem n

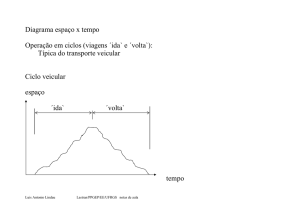
Conjuntos Enumeráveis e Não-enumeráveis
Para quem não esteve na última aula, 25/07, seria bom verificar com os colegas a demonstração do seguinte teorema.
Teorema 1 Todo conjunto X ⊂ N é enumerável, isto é, dado X ⊂ N, teremos X finito ou
existe uma função f : N → X bijetora.
Observação 2 Já vimos, em aula, que o conjunto dos números primos é infinito e, pelo
teorema acima, é enumerável. Fixado número primo p indiquemos por Γp o subconjunto de N
definido por
Γp = {pn ; n ∈ N}.
Como Γp é um subconjunto de N, teremos Γp enumerável. Daı́, teremos
∪
∪
∪
N=
Γp (N \
Γp ).
p primo
p primo
Escrevemos então o conjunto dos números naturais como uma união de uma quantidade infinita
enumerável de conjuntos infinitos enumeráveis dois a dois disjuntos.
Admitiremos, sem demonstração, o teorema abaixo.
Teorema 3 Todo conjunto infinito X possui um subconjunto enumerável infinito.
É interessante observar que o teorema acima nos mostra que, sendo X um conjunto infinito,
existe f ; N → X injetiva, isto é, card(N) ≤ card(X). Logo card(N) é a menor cardinalidade
possı́vel para um conjunto infinito e, portanto, um conjunto X é enumerável se, e somente se,
card(N) < card(X). Lembremos que conhecemos conjuntos enmeráveis, por exemplo, P (N).
Sendo X um conjunto infinito, como temos sempre card(N) ≤ card(X), para concluı́rmos
que X enumerável basta mostrar que card(X) ≤ card(N), isto é, basta mostrarmos que existe
uma função f : X → N injetora. Temos, então, o teorema
Teorema 4 Um conjunto X é enumerável se, e somente se, existe f : X → N injetora.
Proposição 5 O conjunto N × N é enumerável.
Prova. Já exibimos uma função f : N × N → N injetora e, daı́, o resultado segue.
Em alguns momentos uma versão um pouco mais geral do teorema anterior pode ser útil,
qual seja:
1
Teorema 6 Um conjunto X é enumerável se, e somente se, existem um conjunto Y enumerável e uma função f : X → Y injetora. Ou ainda, um conjunto X é enumerável se, e
somente se, existem um conjunto Y enumerável tal que card(X) ≤ card(Y ).
Prova. Será deixada como exercı́cio!
Observação 7 Obervamos que sendo X e Y conjuntos enumeráveis sempre existe uma função
f : X → Y bijetora.(Prove!)
Teorema 8 Sejam X e Y conjuntos enumeráveis. Então:
1) Qualquer subconjunto de X é enumerável
2) X \ Y é enumerável
∩
3) X Y é enumerável
∪
4) X Y é enumerável
5) X × Y é enumerável
Prova.
Será discutida em sala!
Terminamos estas considerações sobre conjuntos enumeráveis com o seguinte teorema.
Teorema 9 Uma união enumerável de conjuntos enumeráveis é ainda um conjunto enumerável.
Exercı́cio 10 1) Sejam A e B conjuntos, f : A → B e g : B → A funções tais que (g◦f )(x) =
x para todo x ∈ A. Mostre que g é sobrejetora e f é injetora.
2) Sejam A, B e C conjuntos tais que card(A) < card(B) e card(B) < card(C). Mostre
que card(A) < card(C).
3) Sejam X um conjunto enumerável e Y um conjunto não-enumerável tais que X ⊂ Y .
Mostre Y \ X é um conjunto não-enumerável.
4) Exibir, justificando, uma função sobrejetora f : N → N tal que f −1 ({n}) seja um
conjunto infinito para todo número natural n.
5) Prove que a função f : N × N → N dada por
f (1, n) = 2n − 1 e f (m + 1, n) = 2m .(2n − 1)
é bijetora.
6) Escreva o conjunto N como união de cinco conjuntos infinitos dois a dois disjuntos.
7) Determine, justificando, um conjunto X tal que card(P (N)) < card(X).
2