Análise Real Simone D. Ramos 1 Lista II de Análise Real

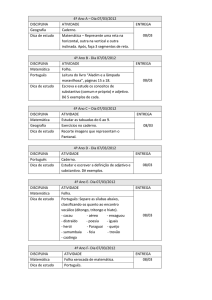
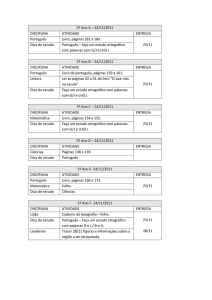
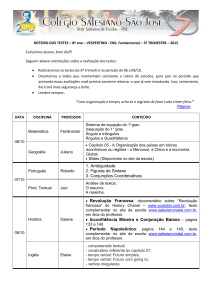
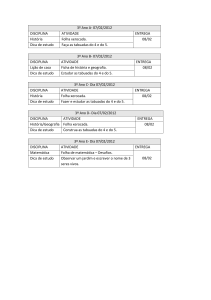
Análise Real
Simone D. Ramos 1
Lista II de Análise Real - Profa. Simone
1. X finito e Y ⊂ X ⇒ card Y ≤ card X.
Notação: card X é o número de elementos de X.
Dica: Usando as dicas encontradas nas páginas finais do livro Análise Real vol. I, mostre
primeiro para X = In e, em seguida, estenda para qualquer conjunto finito.
2. Resultado: A e B finitos e disjuntos ⇒ A ∪ B é finito e card (A ∪ B) = card A + card B.
Use o resultado enunciado acima para mostrar:
(a) X e Y finitos ⇒ card (X ∪ Y ) = card X + card Y − card (X ∩ Y )
Dica: Escreva X e X ∪ Y nas respectivas formas:
X = (X \ Y ) ∪ (X ∩ Y ) e X ∪ Y = (X \ Y ) ∪ Y.
(b) X1 , X2 , . . . , Xn conjuntos finitos dois a dois disjuntos, onde card Xk = mk , ∀1 ≤ k ≤ n ⇒
n
n
n
∪
∑
∑
card( Xk ) =
card Xk =
mk .
k=1
k=1
k=1
Dica: Prove por indução sobre n.
3. Resultado: A finito tal que a /∈A ⇒ P (A ∪ {a}) = 2P (A).
Notação: P (A) denota o conjunto das partes de A, ou seja, o conjunto formado por todos os
subconjuntos de A.
Use o resultado enunciado acima para mostrar:
∅ ̸= X finito ⇒ card (P (X)) = 2card X .
Dica: Prove por indução sobre card X, observando que para qualquer ∅ ̸= A finito, podemos
escolher a ∈ A e escrever A na forma A = (A − {a}) ∪ {a}.
4. ∅ ̸= X ⊂ N, X finito ⇒ ∃x0 ∈ X tal que x ≤ x0 , ∀x ∈ X.
Dica: Defina o conjunto Y = {n ∈ N/n > x, ∀x ∈ X} e mostre que Y possui um elemento
mı́nimo que pode ser escrito na forma t + 1, com t ∈ N.
5. Prove o Princı́pio das Casas de Pombo: m, n ∈ N com m > n ⇒ @ f : Im → In função injetiva
(quando m > n, para alojar m pombos em n casas é preciso que pelo menos uma casa abrigue
mais de um pombo).
Dica: Use as dicas encontradas nas páginas finais do livro Análise Real vol. I.
6. Dados X, Y conjuntos e f : X → Y uma função, prove:
(a) X infinito e f é injetiva ⇒ Y é infinito.
(b) Y infinito e f é sobrejetiva ⇒ X é infinito.
7. X finito e Y infinito ⇒ ∃f : X ⇒ Y função injetiva e ∃g : Y → X função sobrejetiva.
Análise Real
Simone D. Ramos 2
8. Prove que o conjunto P dos números primos é infinito.
Dica: Use as dicas encontradas nas páginas finais do livro Análise Real vol. I.
9. Dê exemplo de uma sequência decrescente X1 ⊃ X2 ⊃ . . . ⊃ Xn ⊃ . . . de conjuntos infinitos
∞
∩
cuja interseção
Xn seja vazia.
n=1
Dica: Tome Xn = {m ∈ N/m > n}
10. X infinito ⇔ X ̸= ∅ e ∀n ∈ N, @f : In → X sobrejetiva.
Dica: Use as dicas encontradas nas páginas finais do livro Análise Real vol. I.
11. Defina f : N × N → N pondo f (1, n) = 2n − 1 e f (m + 1, n) = 2m (2n − 1). Prove que f é uma
bijeção.
Dica: Redefina f : N × N → N por
{
f (m, n) =
2n − 1
se m = 1
2m−1 (2n − 1) se m > 1
e use as dicas encontradas nas páginas finais do livro Análise Real vol. I.
12. Prove que ∃g : N → N sobrejetiva tal que, ∀n ∈ N, g −1 (n) é infinito.
Dica: Além das dicas encontradas nas páginas finais do livro Análise Real vol. I, mostre o
seguinte resultado:
f : A → B sobrejetiva e C infinito tal que C ⊂ B ⇒ f −1 (C) é infinito.
13. Exprima N = N1 ∪ N2 ∪ . . . ∪ Nn ∪ . . . como união infinita de subconjuntos infinitos, dois a dois
disjuntos.
Dica: Tome g : N → N a função considerada no exercı́cio anterior e defina Nn = g −1 (n), ∀n ∈ N.
14. Para cada n ∈ N, seja Pn = {X ⊂ N; card X = n}. Prove que Pn é enumerável. Conclua que
o conjunto Pf dos subconjuntos finitos de N é enumerável.
Dica: Use as dicas encontradas nas páginas finais do livro Análise Real vol. I.
15. Resultado: O conjunto X das sequências (xn ) tais que dado n, xn = 0 ou xn = 1 é não
enumerável.
Use o resultado enunciado acima para mostrar que o conjunto P (N) não é enumerável.
Notação: P (N) denota o conjunto das partes de N.
Dica: Defina a função f : X → P (N) por f (xn ) = {i/xi ̸= 0}, mostre que f é injetiva e use o
resultado acima.
16. Y enumerável e f : X → Y tal que, ∀y ∈ Y, f −1 (y) é enumerável ⇒ X é enumerável.
∞
∪
Dica: Mostre que X pode ser escrito como X =
f −1 (yn ) onde Y = {y1 , y2 , . . . , yn , . . .}.
n=1