descrição de dados

CAPÍTULO 1
DESCRIÇÃO DE DADOS
1.1. Introdução
Em qualquer ciência, engenharia, psicologia, medicina, economia, biologia, etc.,
modelos são usados para descrever fenômenos. Estes modelos são criados com base em um
certo número de dados experimentais. Quando se tenta aplicar estes modelos para descrever
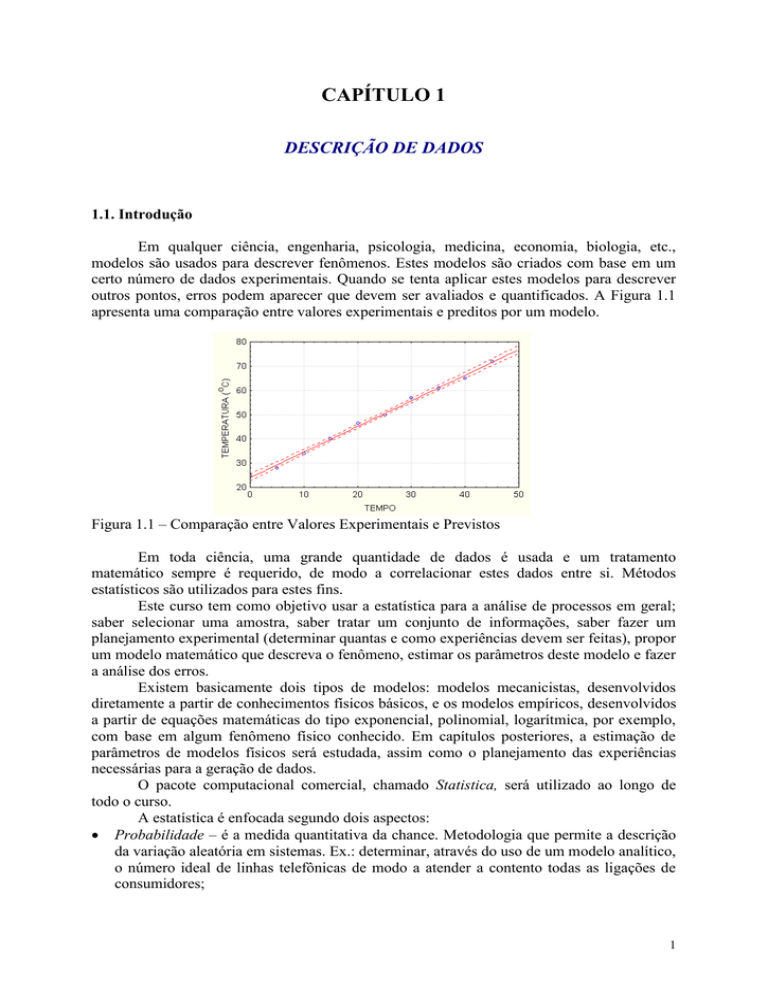
outros pontos, erros podem aparecer que devem ser avaliados e quantificados. A Figura 1.1
apresenta uma comparação entre valores experimentais e preditos por um modelo.
Figura 1.1 – Comparação entre Valores Experimentais e Previstos
Em toda ciência, uma grande quantidade de dados é usada e um tratamento
matemático sempre é requerido, de modo a correlacionar estes dados entre si. Métodos
estatísticos são utilizados para estes fins.
Este curso tem como objetivo usar a estatística para a análise de processos em geral;
saber selecionar uma amostra, saber tratar um conjunto de informações, saber fazer um
planejamento experimental (determinar quantas e como experiências devem ser feitas), propor
um modelo matemático que descreva o fenômeno, estimar os parâmetros deste modelo e fazer
a análise dos erros.
Existem basicamente dois tipos de modelos: modelos mecanicistas, desenvolvidos
diretamente a partir de conhecimentos físicos básicos, e os modelos empíricos, desenvolvidos
a partir de equações matemáticas do tipo exponencial, polinomial, logarítmica, por exemplo,
com base em algum fenômeno físico conhecido. Em capítulos posteriores, a estimação de
parâmetros de modelos físicos será estudada, assim como o planejamento das experiências
necessárias para a geração de dados.
O pacote computacional comercial, chamado Statistica, será utilizado ao longo de
todo o curso.
A estatística é enfocada segundo dois aspectos:
 Probabilidade – é a medida quantitativa da chance. Metodologia que permite a descrição
da variação aleatória em sistemas. Ex.: determinar, através do uso de um modelo analítico,
o número ideal de linhas telefônicas de modo a atender a contento todas as ligações de
consumidores;
1

Inferência Estatística – usa dados de uma amostra para obter conclusões gerais a cerca da
população da qual a amostra foi coletada. Ex.: contar o número de lâmpadas defeituosas
em uma amostra e inferir o número total de lâmpadas defeituosas para todo o lote.
1.2. Amostragem
Como afirmado acima, o estudo da inferência estatística usa o conceito de amostras que
devem ser tiradas de uma população. As conclusões a cerca da população dependem do modo
como a amostra foi selecionada. Esta amostra tem que ser representativa da população. A
maioria das técnicas estatísticas considera que as amostras são aleatórias. Não é fácil obter
uma amostra aleatória. Podem-se usar tabelas de números aleatórios, de modo a gerar
amostras, quando a população é pequena. Associa-se um número a cada elemento da
população e escolhe-se, pela tabela de números aleatórios, um conjunto de números de modo
a gerar uma amostra. Técnicas de amostragem serão analisadas posteriormente.
1.3. Descrição de Dados
Os dados para serem analisados podem ser numéricos ou não; por exemplo: cor dos
olhos, país, datas, idades, número de pessoas com catapora, etc. Estes dados recebem o nome
de variáveis. Estas podem ser discretas ou contínuas. Um exemplo de variável discreta pode
ser o número de irmãos, 0, 1, ...10. Em linguagem mais simples: variável discreta é aquela
que não aceita casa decimal. Um exemplo de variável contínua pode ser o peso de uma
pessoa; pode ser qualquer valor dentro de uma certa faixa. Usando a mesma definição
simplória de antes: variável contínua é aquela que aceita casa decimal.
As variáveis podem ser qualitativas ou quantitativas. As variáveis qualitativas são
aquelas descritas por dados não numéricos, como por exemplo nomes de países, tipos de
catalisador (A, B, C), tipos de máquinas (máquina 1, máquina 2), etc. As variáveis
quantitativas são representadas por um valor numérico, como temperatura, pressão, índice de
inflação, diâmetro de partículas,etc. As variáveis qualitativas podem ser tratadas como
quantitativas caso um número seja conferido à informação; por exemplo, país de nascimento:
Brasil = 1, Bélgica = 2; catalisador A = 1, catalisador B = 2.
Dados coletados através de pesquisas podem ser descritos na forma de tabelas ou de
gráficos. Considere os dados da pressão sangüínea de uma amostra de 10 indivíduos:
Tabela 1.1 – Pressão Sangüínea da Amostra de Indivíduos
1
2
3
4
5
6
7
83
88
90
92
96
103
113
8
114
9
123
10
135
Esses dados podem ser visualizados através de um diagrama de pontos (dot diagram),
conforme Figura 1.2, usado para no máximo cerca de 20 observações, que permite ilustrar o
comportamento de valores individuais em relação ao conjunto desses valores. No caso de se
ter pontos repetidos, estes devem ser colocados um acima do outro, formando uma pilha,
Figura 1.3.
  




Figura 1.2 Diagrama de Pontos




  



Figura 1.3 Diagrama de Pontos com Repetição

2
De modo a interpretar melhor o que esses números exprimem, intervalos devem ser
criados, preferencialmente, igualmente espaçados. O número deles depende do número de
observações e o quão dispersos os dados estão. O número de intervalos deve ser
aproximadamente igual à raiz quadrada do tamanho da amostra (é aconselhável). A
especificação da largura do intervalo é uma consideração importante. Intervalos muito
grandes resultam em menos intervalos de classe. O contrário é verdade.
Tabela 1.2 – Tabela de Distribuição de Freqüência das Pressões Sangüíneas
Intervalo
Ponto
Freqüência
Freqüência Freqüência
Médio
Total=10
Relativa (%) Cumulativa
(%)
87,5
4
40
40
80-95 ou 80  x < 95
102,5
2
20
60
95-110 ou 95  x < 110
117,5
3
30
90
110-125 ou 110  x < 125
132,5
1
10
100
125-140 ou 125  x < 140
A coluna da freqüência representa o número de pessoas que possuem pressão
sangüínea no respectivo intervalo. A freqüência relativa é a informação mais importante, pois
independe do número da amostra. Usando o software Statistica, obtém-se o seguinte
resultado:
Tabela 1.3 - Tabela de Distribuição de Freqüência das Pressões Sangüíneas – Saída do
Statistica
1.
2.
3.
4.
Essa tabela foi obtida através do seguinte procedimento:
Abra o módulo Basic Statistics.
Digite os dados da pressão sangüínea.
Escolha a opção Frequency tables.
A janela a seguir irá aparecer; reproduza-a e depois escolha a opção Frequency tables.
Surgirá uma tabela igual à Tabela 1.2, em que apenas os nomes dos itens foram trocados.
Os dados de freqüência relativa e cumulativa são facilmente visualizados através de
histogramas (Figuras 1.5 e 1.7), principalmente para amostras grandes. A Figura 1.5 foi
obtida no Statistica, escolhendo-se a opção Histograms. A curva vermelha desaparecerá se
você apertar o mouse duas vezes exatamente em cima da curva. Escolha a opção Display off.
O histograma de freqüência cumulativa foi obtido editando-se os dados do gráfico da
freqüência relativa. Pressione o botão direito do mouse que deve estar em cima de algum dos
retângulos do histograma. Escolha a opção Edit this Plot/series Data. Uma janela igual a
Figura 1.6 irá aparecer.
3
Figura 1.4 Janela do Statistica.
5
4
FrequênciaRelativa
3
2
1
0
7
0 7
5 8
0 8
5 9
0 9
51
0
01
0
51
1
01
1
51
2
01
2
51
3
01
3
51
4
0
P
ressão
Figura 1.5 – Histograma para Freqüência Relativa – Caso com 4 Intervalos de Classe.
Figura 1.6 Janela do Statistica
4
FrequênciaCumulativa
Some os dados de Y de modo a ficar com: 4,00; 6,00; 9,00 e 10,00. Escolha a opção
Redraw na barra de ferramentas. A escala do eixo Y deve ser modificada. Clique o mouse
duas vezes em cima de qualquer número da escala Y. Na janela Scaling, coloque o valor 10 no
Max.
1
0
9
8
7
6
5
4
3
2
1
0
6
5
8
0
9
5
1
1
0
P
ressão
1
2
5
1
4
0
Figura 1.7 – Histograma para Freqüência Cumulativa – Caso com 4 Intervalos de Classe
A influência do número de intervalos de classe pode ser verificada através da Figura
1.8, gerada pelo Statistica, que usa 5 intervalos de classe. Devido a esse fato, todos os
resultados apresentados a seguir se baseiam nessa informação. O gráfico a
3
FrequenciaRelativa
2
1
0
7
0
8
0
9
0
1
0
0
1
1
0
1
2
0
1
3
0
P
ressao
Figura 1.8 – Histograma para Freqüência Relativa – Caso com 5 Intervalos de Classe
seguir foi gerado no módulo Basic Statistics, na opção Descriptive Statistics, obtendo-se a
Figura 1.9. Na realidade, a opção Frequency tables, usada anteriormente só precisa ser
considerada se se quiser adotar o número de intervalos de classe escolhido por nós.
Se os pontos médios dos retângulos forem conectados por uma linha reta, ou se forem
conectados por uma curva suave, o polígono de freqüência é encontrado, como mostrado na
Figura 1.10 ou na Figura 1.11. A linha da Figura 1.10 foi obtida pressionando o botão direito
do mouse e escolhendo-se a opção Change Plot Layout(s). Reproduza a janela apresentada na
Figura 1.12. No caso da linha da Figura 1.11, a janela deverá ter a aparência apresentada na
Figura 1.13.
5
Figura 1.9 Janela do Statistica quando a opção Descriptive satatistics for escolhida.
3
FrequenciaRelativa
2
1
0
7
0
8
0
9
0
1
0
0
1
1
0
1
2
0
1
3
0
P
ressao
Figura 1.10 – Polígono de Freqüência
6
3
FrequenciaRelativa
2
1
0
7
0
8
0
9
0
1
0
0
1
1
0
1
2
0
1
3
0
P
ressao
Figura 1.11 – Polígono de Freqüência Suavizado
Figura 1.12 Janela do Statistica para a geração da linha da Figura 1.10.
Histogramas podem ser usados com dados qualitativos, como categorias de uma classe
(homem, mulher ou ensinos fundamental, médio e superior). Um histograma de ocorrências
por categoria (em que as categorias são ordenadas pelo número de ocorrências) é chamado de
gráfico Pareto. Este tipo de gráfico é muito usado em controle de qualidade; por exemplo,
pode-se plotar o número de defeitos produzidos em uma determinada peça. No histograma, os
fatos que ocorrerem com maior freqüência devem ficar sempre mais à esquerda na abscissa,
de modo que se possa identificar facilmente aquele item que causa maior custo ou defeito.
Existe um dogma associado ao princípio de Pareto (V. Pareto, economista italiano): uma
minoria de fatores causa a maioria dos problemas. A Figura 1.14 apresenta um exemplo do
gráfico de Pareto.
7
Figura 1.13 Janela do Statistica para a geração da linha da Figura 1.11.
1
0
0
8
0
6
0
4
0
2
0
0
Percentagem
Sold._Insuficient
Sold._Cold_Joint
Sold._Opens
Comp._Improper_1
Sold._Splater
TST_Mark_White_Mark
Tst._Mark_EC_Mark
Raw_CD_Shroud_Re.
Comp._Extra_Part
Comp._Mising
Comp._Damaged
Stamping_Oper_ID
Stamping_Mising
Sold._Short
Wire_Incorrect
Raw_Cd_Damaged
Valores
1
0
0
9
0
8
0
7
0
6
0
0
5
0 4
4
0
2
0
3
0
2
0
7 6 5 3 3 3 2 2 2 1 1 1 1 1
1
0
0
C
ategorias(variavel:N
enhum
D
efeito)
V
alor
P
ercentagem
C
um
ulativa
Figura 1.14 – Gráfico de Pareto – Defeitos em um Circuito
Há uma outra forma de correlacionar dados. Por exemplo, o peso e a pressão
sangüínea de uma série de pessoas podem ser relacionados através do gráfico de dispersão
(scatter diagram), Figura 1.15. Pode ser visto que não existe uma tendência de
comportamento. Esse gráfico foi construído através da opção Graphs, existente na barra de
ferramentas. Escolheu-se Stats 2D Graphs e Scatterplot, obtendo-se a janela da Figura 1.16.
As variáveis devem ser selecionadas.
8
P
E
S
O
v
s.P
R
E
S
S
Ã
O
P
R
E
S
S
Ã
O
=9
1
,5
6
8+,1
6
8
6
6*P
E
S
O
C
o
rrelação
:r=0
,1
6
6
0
3
1
3
0
1
2
0
PRESSÃO
1
1
0
1
0
0
9
0
8
0
4
0
5
0
6
0
7
0
P
E
S
O
8
0
9
0
1
0
0
Figura 1.15 – Diagrama de Espalhamento ou Dispersão (Scatter Diagram)
Figura 1.16 Janela do Staistica para a construção da Figura 1.15.
A descrição numérica dos dados apresentados anteriormente é feita através do uso de
certos índices, chamados estatísticas, dados a seguir.
1.3.1 Medidas da Tendência Central
i) Média Aritmética (Sample Mean) ou Primeiro Momento da Amostra:
n
Xi
(1)
n
i
onde n é o número total de dados. Para o exemplo dado, a média é 103,7. Se os dados forem
representados em termos de freqüência, fica-se com:
X 
p
X 

i 1
p
fi X i
p
f
i 1

f X
i 1
i
n
i
(2)
i
9
em que p é o número de intervalos de classe, Xi é o valor médio do intervalo de classe que
corresponde à freqüência fi. A Equação (2) é a média ponderada. Para os dados de pressão, a
média ponderada é igual a 104, valor esse muito próximo da média aritmética.
ii) Média Geométrica: usada em economia; é sempre menor que a média aritmética.
X  n X 1 X 2 ... X n
(3)
Ex.: Uma empresa se expande 10% no primeiro ano, 20% no segundo ano e 50% no terceiro
ano. Qual é a taxa anual média de expansão ?
X  3 1,1 *1,20 *1,5  3 1,98  1,256
iii) Média Harmônica:
X 
n
1
1
(4)
Xi
n
i 1
Ex.: Você pega uma amostra a cada tempo de um lote de material até que você encontra um
item com defeito. A primeira vez você consegue uma peça com defeito, após 200 tentativas.
Na segunda vez, você tenta 300 e na terceira, 400 vezes. Qual o número médio itens
defeituosos que você espera encontrar ?
Solução: É importante ter amostras do mesmo tamanho. A primeira amostra tem 0.5% das
peças com defeito. A segunda tem 0,33% e a terceira tem 0,25%. A média de defeitos na
amostra de tamanho 100 é (0,5+0,3333+0,25)/3=0,361. A média harmônica será:
3600 (itens bons)
3
X 

 276,92
1 / 200  1 / 300  1 / 400 13 (itens defeituosos)

iv) Moda: a moda corresponde ao dado que tem maior freqüência; ou seja, que mais ocorre.
Se existirem dois valores com igual número de ocorrência, diz-se que a distribuição é
bimodal; para mais de dois valores, tem-se a distribuição multimodal. Quando não há um
valor que ocorra com mais freqüência, então esta distribuição não tem moda. No exemplo
dado, não existe moda. Porém, quando os dados são expressos no histograma, a moda é igual
a 87,5, correspondendo ao valor médio do maior pico. A moda não é uma boa medida da
tendência central, visto que ela depende do grupo de dados; ou seja, depende de como os
dados são agrupados. Para os dados na forma da Tabela 1.2, tem-se:
 a 
MO  LMO  
(5)

ab
sendo LMO o limite inferior da classe modal (o intervalo com a maior freqüência), a é o valor
absoluto da diferença na freqüência entre a classe modal e a classe precedente, b é o valor
absoluto da diferença na freqüência entre a classe modal e a classe seguinte e  é a largura da
classe modal.
v) Mediana: é o ponto que divide a amostra em duas metades. Por exemplo, tendo-se um
conjunto de observações, tal qual: 10, 50, 25, 60 e 45, a mediana é igual a 45, depois de
rearranjar em ordem crescente os dados. O número 45 divide ao meio a amostra. No exemplo
dado anteriormente, tem-se um número par de dados. Neste caso, deve-se fazer a média
aritmética entre o valor correspondente ao meio do intervalo e o valor imediatamente
posterior. Assim, a mediana é igual a 99.5. A fórmula geral é:
10
 X ( n 1) / 2  n  ímpar

M   X n / 2  X ( n / 21)
 n  par

2

(6)
Em termos de freqüência, fica-se com:
 n 1

T 


(7)
M  LM   2
 fM 




em que LM é o limite inferior do intervalo contendo a mediana (chamado a classe mediana),
fM é a freqüência na classe mediana, T é o total de todas as freqüências nos intervalos
precedendo a classe mediana e  é a largura da classe mediana.
A mediana tem a vantagem de não ser muito influenciada pelos valores extremos. Por
exemplo, considere a seguinte amostra: 1,2,3,4,6,7 e 8. A média é igual a 4,43 e a mediana é
igual a 4. Mas se ao invés de 6 o valor for 2.519, a média será 363,43 e a mediana continuará
a ser 4.
Se os dados são simétricos, então a média, a mediana e a moda coincidem, Figura
1.17; porém, se a distribuição for assimétrica, essas estatísticas não coincidem, ficando-se
com uma distribuição assimétrica para a esquerda (negativamente assimétrica) e uma
distribuição assimétrica para a direita (positivamente assimétrica), conforme Figuras 1.18 e
Figura 1.19, respectivamente.
9
8
7
6
Frequência
5
4
3
2
1
0
5
1
0
1
5
2
0
2
5
3
0
3
5
4
0
4
5
FrequênciaRelativa
Figura 1.17 – Distribuição Simétrica
2
0
1
8
1
6
1
4
1
2
1
0
8
6
4
2
0
1
0
1
5
2
0
2
5
3
0
3
5
4
0
Figura 1.18 – Distribuição Assimétrica para a Esquerda (Negativamente Assimétrica)
11
FrequênciaRelativa
2
0
1
8
1
6
1
4
1
2
1
0
8
6
4
2
0
1
0
1
5
2
0
2
5
3
0
3
5
4
0
Figura 1.19 – Distribuição Assimétrica para a Direita (Positivamente Assimétrica)
vi) Quartis: são os pontos que dividem a amostra (em ordem crescente) em 4 partes iguais;
assim, tem-se o quartil de 25% (quartil inferior), o quartil de 50% (a própria mediana) e o
quartil de 75% (quartil superior). Por exemplo, para o conjunto de observações 30, 54, 78,
102, 165 e 180, os quartis de 25% e de 75% são iguais a 54 e 165, respectivamente. Ou seja,
25% dos dados estão abaixo de 54 e 75% dos dados estão abaixo de 165. Quando o número
de observações não permitir uma divisão em duas e três partes iguais, há diferentes maneiras
de calcular os quartis. O Statistica usa as seguintes maneiras:
a) p%  (1  g )  x j  g  x j 1
onde j é a parte inteira do produto n p (=j+g) e g é a
parte fracionária desse produto; n é o número de dados da amostra e p é o valor do quartil de
interesse (25% ou 75%). Para os dados da Tabela 1.1, tem-se:
n  p  10 * 0,25  2,5  j  g ;
n  p  10 * 0,75  7,5  j  g
logo, j=2 (e j=7)e g=0,5 (e g=0,5). Assim, x2=88 (x7=113) e x3=90 (x8=114), ficando-se com:
25%  (1  0,5)  88  0,5  90  89
75%  (1  0,5)  113  0,5  114  113,5
b) p%  (1  g )  x j  g  x j 1
tem-se:
com
(n  1)  p  j  g . Para os dados da Tabela 1.1,
(n  1)  p  (10  1) * 0,25  2,75  j  g
(n  1)  p  (10  1) * 0,75  8,25  j  g
25%  (1  0,75)  88  0,75  90  89,5
75%  (1  0,25)  113  0,25  114  113,25
c) p %  x j
p %  x j 1
se g=0
com j=2 e g=0,75
com j=8 e g=0,25
sendo n p=j+g
se g>0
Para os dados da Tabela 1.1, tem-se que: 25% = 90 e 75% = 114.
Todas as três maneiras deram valores muito próximos. Existem outras formas de
calcular os quartis; para maiores detalhes, procurar bibliografia complementar.
12
Os valores da média, da mediana e dos quartis são apresentados na Tabela 1.4, obtida
do Statistica quando a opção Detailed descriptive statistics foi escolhida na janela mostrada
na Figura 1. 9, com a caixa Median & quartiles marcada.
Tabela 1.4 – Valores da Média e da Mediana
1.3.2 Medidas de Dispersão
Às vezes a medida da tendência central não fornece informação suficiente. O exemplo
abaixo ilustra a importância de um índice de dispersão.
Amostra 1: 230 250 245 258 265 240
Amostra 2: 190 228 305 240 265 260
Média Aritmética: 248 psi. A amostra 2 é bem mais dispersa.
i) Variância ou Segundo Momento da Amostra:
n
s2 
_
 ( X i  X )2
i 1
(8)
n 1
A razão para o denominador ser igual a n-1 é devido ao grau de liberdade do sistema
ser igual a n-1. Se o denominador fosse igual a n e se n = 1, não haveria dispersão a ser
computada.
Para grupo de dados, fica-se com:
 p

  f i X i 
i 1

f i X i2  
n
n 1
n
s2 

i 1
2
s  s2
ii) Desvio-padrão:
(9)
(10)
iii) Amplitude (Sample Range): fácil de calcular, mas só calcula informação entre os
valores extremos. Para amostras com menos de 10 observações, isto não é problema. Para o
exemplo em questão, a faixa de amostra seria igual a 35, para o primeiro caso, e 115 para o
segundo, mostrando assim que a segunda amostra tem maior variabilidade.
R  max( X i )  min( X i )
(11)
iv) Covariância: é uma média dos produtos dos desvios da média.
n
 XY 
(X
i 1
i
 X )(Yi  Y )
n 1
(12)
13
Covariância negativa significa grandes valores de X associados com pequenos valores
de Y e vice-versa. A covariância depende da unidade das variáveis. Esta dependência é
eliminada quando a covariância é dividida pelo produto dos desvios-padrão das variáveis,
resultando no coeficiente de correlação, definido abaixo.
v) Coeficiente de Correlação: mede o grau de associação entre duas variáveis
n
r
( X
i 1
i
 X )( Yi  Y )
n
2
 ( X i  X ) 
 i 1

1/ 2
n
2
 ( Yi  Y ) 
 i 1

1/ 2
(13)
O coeficiente de correlação nunca pode ser menor que –1 e maior que 1.
Os valores da variância, do erro-padrão, da amplitude, de máximo e mínimo e da
amplitude dos quartis são apresentados na Tabela 1.5. O erro-padrão é definido como o
desvio-padrão dividido pela raiz quadrado do número de observações. Todos esses valores
foram obtidos utilizando a opção More statistics e selecionando-se todas aquelas de interesse.
Tabela 1.5 – Várias informações obtidas do Statistica.
Uma outra forma gráfica de apresentar os dados é o chamado diagrama de caixa (box
plot) ou diagrama de caixa e linhas (box and whiskers), que permite descrever
simultaneamente vários fatores importantes de uma série de dados, tais como a tendência
central (média ou mediana), a dispersão (desvio-padrão), a possibilidade de detectar outliers
(pontos bastante diferentes do conjunto de dados) e o desvio da simetria. A Figura 1.20
apresenta um exemplo deste tipo de gráfico. O Statistica permite 4 diferentes visualizações,
de acordo com a estatística escolhida. No geral, tem-se que as retas verticais podem
representam os valores máximo e mínimo do conjunto de dados (faixa da amostra) ou o
desvio-padrão ou erro-padrão; o ponto central representa a média ou mediana e as retas
horizontais que formam a caixa representam o quartil 25% (reta inferior) e o quartil 75% (reta
superior), respectivamente.
130
120
110
100
90
80
P
R
E
S
S
A
O
M
ax=125
M
in=83
75%
=114
25%
=90
M
edian=99,5
Figura 1.20 - Diagrama de Caixa – Tipo 1
14
120
115
110
105
100
95
90
85
P
R
E
S
S
A
O
±
1.00*S
td.D
ev.
S
td.D
ev.=15,15879
±
1.00*S
td.E
rr.
S
td.E
rr.=4,793633
M
ean=102,7000
Figura 1.21 - Diagrama de Caixa – Tipo 2
140
125
110
95
80
65
P
R
E
S
S
A
O
±
1.96*S
tD
ev
±
1.00*S
td.D
ev.
S
td.D
ev.=15,15879
M
ean=102,7000
Figura 1.22 - Diagrama de Caixa – Tipo 3
114
110
106
102
98
94
90
P
R
E
S
S
A
O
±
1.96*S
td.E
rr.
±
1.00*S
td.E
rr.
S
td.E
rr.=4,793633
M
ean=102,7000
Figura 1.23 - Diagrama de Caixa – Tipo 4
15
2
,5
2
,5
2
,0
2
,0
1
,5
1
,5
1
,0
1
,0
0
,5
0
,5
0
,0
0
,0
-0
,5
-0
,5
Janeiro
Fevereiro
Marco
Abril
Maio
Junho
Julho
Agosto
Setembro
Outubro
Novembro
Dezembro
Inflação
Quando uma das variáveis é o tempo, a dispersão é analisada através do gráfico
sequencial ou em linha. A abscissa corresponde ao tempo em que um evento (escala vertical)
ocorre. Dessa forma, tendências podem ser facilmente detectadas, como pode ser visualizado
pela Figura 1.24.
M
eses
Figura 1.24 – Gráfico Sequencial
1.3.3 Medidas de Desvio da Normalidade
a) Simetria: o desvio da simetria de uma distribuição pode ser medido através de uma
estatística chamada skewness (termo proposto por Pearson em 1895). A fórmula de
cálculo é dada a seguir:
n
Skewness 
n  ( xi  x ) 3
i 1
(14)
(n  1)( n  2) 3
em que n = número de pontos experimentais, xi = valor do i-ésimo ponto experimental,
x = média dos pontos experimentais e 2 = variância da população.
b) Kurtosis: mede o achatamento/alongamento da curva de uma distribuição. Se o valor da
kurtosis for igual a zero, então a distribuição será normal. A distribuição será mais
achatada ou mais alongada, dependendo se o valor da kurtosis for negativo ou positivo,
respectivamente. O cálculo dessa estatística é dado a seguir.
2
n


 n
4
2
n(n  1) ( xi  x )  3(n  1)  ( xi  x )  
i 1
 i 1
 

(15)
Kurtosis  
4
(n  1)( n  2)( n  3)


16
1.4 Exercícios
1.1 Os seguintes dados são as temperaturas, em dias consecutivos, do efluente na descarga de
uma unidade de tratamento de esgoto:
43
47
51
48
52
50
46
49
45
52
46
51
44
49
46
51
49
45
44
50
48
50
49
50
(a)
Calcule a média, a mediana, a variância e o desvio-padrão da amostra.
(b)
Construa um diagrama de caixa dos dados e comente sobre a informação obtida aí.
(c)
Você poderia afirmar que a amostra é proveniente de uma população normal?
1.2 Os seguintes dados são os números de ciclos até falhar, de corpos de prova de alumínio,
sujeitos a uma tensão alternada repetida, de 21.000 psi e 18 ciclos por segundo.
a) Construa uma distribuição de freqüências e histograma.
b) Encontre a mediana e os quartis inferior e superior.
1.3 Considere as duas amostras dadas abaixo:
Amostra 1: 10; 9; 8; 7; 8; 6; 10 e 6.
Amostra 2: 10; 6; 10; 6; 8; 10; 8 e 6.
(a)
Calcule a amplitude para ambas amostras. Você concluiria que ambas amostras
exibem a mesma variabilidade? Explique.
(b)
Calcule o desvio-padrão de ambas amostras. Essas quantidades indicam que ambas
amostras têm a mesma variabilidade? Explique.
(c)
Escreva um curto texto contrastando a amplitude da amostra com o desvio-padrão
da amostra, como medida de variabilidade.
1.4 Um artigo em Quality Engineering (Vol. 4, 1992, p. 487-495) apresenta dados de
viscosidade de um processo químico em batelada. Uma amostra desses dados é apresentada a
seguir.
(a)
Considere a noção de que as 40 primeiras observações foram geradas a partir de
um processo específico, enquanto que as 40 últimas observações foram geradas a
partir de um processo diferente. O gráfico indica que os dois processos geram
resultados similares?
(b)
Calcule a média e a variância das 40 primeiras observações; então, calcule esses
valores para as 40 últimas observações. Essas quantidades indicam que ambos os
17
processos resultam no mesmo nível de média? E a mesma variabilidade?
Explique.
1.5 A percentagem de algodão no material usado para fabricar camisas de homens é dada a
seguir. Encontre a mediana, a moda e a média da amostra dos dados no Exercício 2-3.
Explique como essas três medidas de localização descrevem diferentes características dos
dados.
18