Slide 1 - Prof. Saulo Almeida

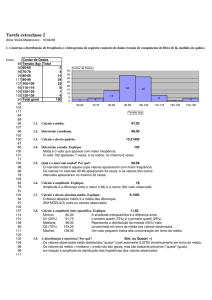
São valores que ocupam determinados lugares de uma série ordenada (rol).
TIPOS:
Quartis
Decis
Percentis
Quartis
Corresponde aos valores de uma série que dividem a distribuição em quatro
partes iguais.
O cálculo de qualquer um dos quartis ocorre de forma idêntica ao cálculo da
mediana, substituindo-se, na fórmula desta, apenas a posição em que se
encontra o elemento desejado.
Quartis
Primeiro Quartil (Q1)
Valor situado de tal modo na série que uma quarta parte (25%) dos dados é
menor que ele e as três quartas partes restantes (75%) são maiores.
25%
75%
Q1
Quartis
Segundo Quartil (Q2)
Valor situado de tal modo na série que a metade (50%) dos dados é menor
que ele e a outra metade (50%) é maior.
50%
50%
Q2 = Md
Decis
Divide a distribuição em dez partes iguais em um conjunto ordenado de
valores.
Pode-se ter, assim, D1, D2, D3, ..., D10.
Decis
Dados Não-Agrupados
A posição do elemento decil no conjunto ordenado é identificado pela
seguinte expressão:
i ( N  1)
Di 
10
Di = posição do elemento desejado
i = {1, 2, 3, ..., 9}
N = nº de observações
Percentis
É a divisão de um conjunto ordenado em cem partes iguais.
Pode-se ter, assim, P1, P2, P3, ..., P100.
Percentis
Dados Não-Agrupados
A posição do elemento percentil no conjunto ordenado é identificado
pela seguinte expressão:
i ( N  1)
Pi 
100
Pi = posição do elemento desejado
i = {1, 2, 3, ..., 99}
N = nº de observações
Visam apresentar o grau de homogeneidade ou heterogeneidade
que existe entre os valores que compõem o conjunto.
As medidas de dispersão são baseadas nos valores obtidos a partir
das medidas de tendência central.
ABSOLUTAS
RELATIVAS
Amplitude Total
Corresponde à diferença entre o maior e o menor dos valores de uma
distribuição.
AT = x(máx) – x(min)
Quanto maior o número de observações, maior tende a ser sua
amplitude.
Amplitude Total
Dados Não-Agrupados
Exemplo: Dados os valores 40, 45, 48, 52, 54, 62 e 70
AT = x(máx) – x(min)
AT = 70 – 40
AT = 30
Quanto maior o AT maior a dispersão dos valores da variável
Amplitude Total
QUANDO UTILIZAR?
1. Quando se busca determinar a diferença entre os valores máximo e
mínimo em uma determinada época ou período.
2. Como uma medida rápida de variabilidade dos dados, que não
demonstre muita preocupação com a exatidão e a estabilidade.
3. Quando a distribuição de valores estiver mantendo uma certa
homogeneidade.
4. É utilizada como um índice preliminar.
Amplitude Total
LIMITAÇÕES
1. É uma medida de dispersão que, ao não considerar o conjunto de
valores intermediários, reduz a confiança dos resultados obtidos.
2. Não são muito utilizadas, pois são instáveis, deixando-se influenciar
pelos valores extremos da distribuição.
3. Possui uma aplicação restrita a distribuições de resultados mensurados
em nível pelo menos intervalar.
Desvio Médio
É a média aritmética dos valores absolutos dos desvios da distribuição,
em relação a uma medida de tendência central (média ou mediana).
X X

Dm 
N
Dm = desvio médio

X  X  Somatório dos
desvios absolutos
N (fi)= número total de
escores
Dados Não-Agrupados
Desvio Médio
Exemplo: Dados os valores 2, 5, 8, 15, 20.
2  5  8  15  20
X
 10
5
X X

Dm 
N
Dm 
2  10  5  10  8  10  15  10  20  10
5
Dm  6
Desvio Médio
VANTAGENS
1. Depende de todos os valores da distribuição, fazendo com que seu
resultado apresente maiores seguranças em relação à Amplitude Total
e Desvio Quartílico.
2. Seu cálculo pode ser efetuado a partir da média e da mediana.
3. Não leva em consideração a existência de desvios negativos, pois seu
cálculo é medido em termos modulares (absolutos).
4. Poderá substituir o Desvio Padrão, quando este for influenciado
indevidamente pelos desvios extremos.
Desvio-Padrão
Corresponde à raiz quadrada da média aritmética dos quadrados
dos desvios.
s
x  x 
2
i
n
É a medida de dispersão mais utilizada na comparação de
diferenças entre conjuntos de dados.
Determina a dispersão dos valores em relação à média.
Desvio-Padrão
QUANDO UTILIZAR?
1. Para avaliar o grau de variabilidade em uma distribuição ou para
comparar a variabilidade de diferentes distribuições.
2. Para ajustar a posição relativa de escores individuais dentro de
uma distribuição.
Desvio-Padrão
CURVA NORMAL
Quando:
X  80
s5
Desvio-Padrão
COMO INTERPRETAR?
REGRA EMPÍRICA
A regra 68-95-99 para Dados Distribuição Normal
• Cerca de 68% dos valores estão a menos de 1 desviopadrão a contar da média.
• Cerca de 95% dos valores estão a menos de 2 desviospadrão a contar da média.
• Cerca de 99,7% dos valores estão a menos de 3 desviospadrão a contar da média.
Desvio-Padrão
COMO INTERPRETAR?
Desvio-Padrão
COMO INTERPRETAR?
Desvio-Padrão
QUANDO UTILIZAR?
1. Para avaliar o grau de variabilidade em uma distribuição ou para
comparar a variabilidade de diferentes distribuições.
2. Para ajustar a posição relativa de escores individuais dentro de
uma distribuição.
Variância
Corresponde à média dos quadrados dos desvios
(quadrado do desvio padrão).
A variância é uma medida que tem pouca utilidade como
estatística descritiva.
Variância
QUANDO UTILIZAR?
1. Para testes estatísticos dentro da inferência estatística e em
combinações de amostras.
2. Em processos estatísticos avançados.
3. Quando os valores absolutos obtidos a partir do desvio médio
não possuem utilidade.
Refere-se à forma da curva de uma distribuição de freqüências,
mais especificamente do polígono de freqüências ou do histograma.
Uma distribuição com classes é simétrica quando:
Média = Mediana = Moda
Assimétrica à esquerda ou negativa quando:
Média < Mediana < Moda
Assimétrica à direita ou positiva quando:
Média > Mediana > Moda
Curva Assimétrica à esquerda ou negativa
Média < Mediana < Moda
Curva Assimétrica à direita ou positiva
Média > Mediana > Moda
Curva Simétrica
Média = Mediana = Moda
TIPOS DE ASSIMETRIA
X  Mo
X  Mo  0
assimetria nula ou distribuição simétrica
X  Mo  0
assimetria negativa ou à esquerda
X  Mo  0
assimetria positiva ou à direita
Igor Menezes
Estatística
Igor Menezes
Estatística
TIPOS DE CURTOSE
Quando a distribuição apresenta uma curva de freqüência mais
fechada que a normal (ou mais aguda em sua parte superior).
TIPOS DE CURTOSE
Quando a distribuição apresenta uma curva de freqüência mais
aberta que a normal (ou mais achatada em sua parte superior).
TIPOS DE CURTOSE
Corresponde à curva normal.