Laboratório de Estrutura da Matéria II

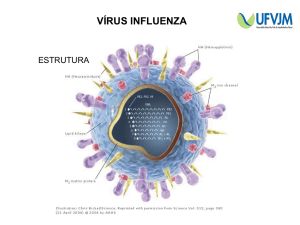
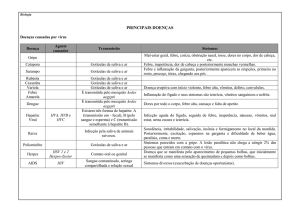
Laboratório de Estrutura da Matéria II
Experiência de Millikan
PRINCÍPIO E OBJETIVOS
O movimento de gotículas de óleo eletricamente carregadas sujeitas a um campo elétrico e ao campo
gravitacional é investigado e as velocidades das gotículas são determinadas por medidas diretas dos tempos
de subida e descida. A carga elementar é então obtida a partir da medida das cargas elétricas de uma grande
quantidade de gotículas.
TÓPICOS RELACIONADOS
Carga elétrica, campo eletrostático, diferença de potencial, capacitores, viscosidade, lei de Stokes, empuxo,
movimento uniforme, quantização da carga elétrica.
EQUIPAMENTO
Aparato de Millikan (contendo borrifador, reservatório de óleo, sistema de alimentação de óleo, capacitor,
microscópio de observação, lâmpada, suporte, etc), fonte de tensão, voltímetro, escala micrométrica de
calibração, lâminas de vidro, comutador elétrico, cabos de conexão, cronômetro, nível de bolha de ar.
TAREFAS EXPERIMENTAIS
1. Medir as velocidades de subida e descida de várias gotículas de óleo eletricamente carregadas com
diferentes quantidades de carga elétrica e submetidas a diferentes tensões eletrostáticas.
2. Determinar os raios e as cargas elétricas das gotículas analisadas e verificar a quantização da carga.
3. Determinar a carga elétrica elementar a partir da análise estatística das cargas de um grande número
de diferentes gotículas.
PROCEDIMENTOS EM LABORATÓRIO
1. O arranjo experimental encontra-se esquematizado na Fig. 1. A fonte de tensão fornece a tensão
necessária para a iluminação do campo de observação e também para a aceleração das gotículas
eletricamente carregadas. Observe que a lâmpada deve ser conectada à saída de tensão de 6,3 V da
fonte.
2. A conexão em série das saídas de tensão contínua fixa (300 V) e variável (0 a 300 V) da fonte de
alimentação permite a obtenção de tensões de 300 a 600 V entre as placas do capacitor no aparato de
Millikan. A polaridade dessa tensão pode ser invertida com uso do comutador. As conexões elétricas
1
envolvidas encontram-se indicadas na Fig. 2. Verifique atentamente e procure compreender todas
essas conexões.
Fig. 1: Arranjo experimental para realização da experiência de Millikan.
Fig. 2: Conexões elétricas para alimentação do capacitor no aparato de Millikan.
3. Antes de iniciar as medições é necessário verificar o nivelamento do aparato, de tal forma que as
placas do capacitor estejam na horizontal (isso garante que o campo elétrico a ser aplicado entre as
placas possuirá a mesma direção do campo gravitacional). Utilize o nível de bolha para fazer essa
verificação, ajustando os pés do aparato de Millikan se necessário.
4. Acione a fonte de tensão com os cabos de alimentação das placas do capacitor desconectados, de
modo que apenas a lâmpada de iluminação da câmara no aparato de Millikan esteja alimentada.
2
5. O movimento das gotículas é visualizado através do microscópio montado no aparato de Millikan.
Com auxílio de uma câmera de vídeo, a imagem das gotículas é observada em um monitor de TV,
sendo a distância percorrida pelas gotículas medida com uso da escala gravada no monitor.
6. Para correta medida das distâncias percorridas pelas gotículas, é necessário efetuar um procedimento
de calibração da distância entre os traços de referência marcados no monitor. Para isso, introduza
diante do microscópio uma lâmina contendo a escala micrométrica de calibração. Ajuste a orientação
dessa lâmina para permitir que os traços da escala de calibração fiquem paralelos aos traços de
referência no monitor.
7. Registre a relação entre as divisões nas duas escalas e obtenha assim o fator de calibração da escala
de medição. É recomendável repetir algumas vezes este processo, inclusive em diferentes aulas, para
verificar a reprodutibilidade do fator de calibração.
8. Borrife uma quantidade de óleo dentro da câmara e observe o movimento das gotículas através do
monitor. A posição do microscópio como um todo pode ser agora ajustada para a focalização de
cada gotícula individualmente.
9. Se as gotículas exibirem deslocamentos laterais (fora da vertical) será necessário reajustar o
nivelamento do aparato. Caso o movimento apresente turbulências, a abertura da câmara localizada
em frente ao microscópio deverá ser bloqueada com uma lâmina de vidro transparente.
10. Aplique uma tensão entre 300 e 500 V ao capacitor, borrife nova quantidade de óleo e observe o
movimento das gotículas.
11. Selecione uma gotícula cujo movimento possa ser alterado com mudança na polaridade do capacitor,
ou seja, uma gotícula que inverta o sentido do movimento quando o comutador for acionado.
12. Observe o movimento de descida dessa gotícula entre duas marcas quaisquer na escala de referência.
Marque com o cronômetro digital o tempo que a gotícula leva para percorrer tal distância no
movimento de subida.
13. Inverta a polaridade com o comutador, observe novamente a subida da gotícula e repita a medida
anterior entre 5 e 10 vezes, reajustando o foco do microscópio se necessário. (Não esqueça de zerar o
cronômetro entre cada par de medições consecutivas!)
14. Ainda com a mesma gotícula repita o procedimento anterior, mas agora medindo o tempo de descida
para um total de 5 a 10 percursos consecutivos.
15. Se houver variações bruscas ao longo das seqüências de tempos de subida (ou descida) medidos para
uma dada gotícula, isso significa que houve alteração na sua carga durante o processo de medição.
Assim, os dados referentes a essa gotícula só poderão ser aproveitados (para cálculos de médias) até
o ponto onde ocorreu a mudança.
16. Evite trabalhar com gotículas com movimento muito rápido, já que estas apresentarão cargas
elevadas e não servirão ao propósito de verificação da quantização da carga.
3
17. Evite também trabalhar com gotículas que se movam muito vagarosamente ou cujo movimento
apresente flutuações consideráveis (movimento browniano). A tensão aplicada poderá ser aumentada
(desde que fique inferior a 500 V) para reduzir essas flutuações.
18. Repita todo o processo acima, selecionando uma nova gotícula e analisando seu movimento de
subida e descida. Modifique também a tensão aplicada ao capacitor na análise de diferentes
gotículas. Efetue ao todo medidas para no mínimo 50 diferentes gotículas.
Obs.: Para o bom desenvolvimento desta prática, é fundamental que sejam analisadas gotículas
contendo diferentes quantidades de cargas elétricas elementares. Recomenda-se portanto que após cada
série de medidas sejam calculados os valores das cargas das gotículas analisadas naquela série, de modo
que o grupo possa perceber se tais valores estão se repetindo em torno de uma média comum ou estão
cobrindo uma extensão maior de valores de cargas elétricas (o que é desejado). Assim, o grupo poderá
decidir pela escolha de diferentes parâmetros experimentais (tempo de subida, tempo de descida e tensão
aplicada) na seleção das próximas gotículas a serem analisadas, a fim de conseguir analisar um número
razoável de gotículas possuindo diferentes quantidades de cargas elétricas elementares.
CUIDADOS QUE DEVEM SER TOMADOS EM LABORATÓRIO
1. Não permita jamais que a tensão aplicada ao capacitor ultrapasse 500 V.
2. Mantenha sempre as gotículas a serem observadas em foco, de modo a evitar erros de paralaxe na
análise do movimento das gotículas.
3. Evite tocar nas superfícies das lentes ou das placas transparentes no aparato de Millikan.
4. Opere o comutador com cuidado, uma vez que estão sendo aplicadas tensões elevadas.
FUNDAMENTAÇÃO TEÓRICA
1. O movimento das gotículas pode ser totalmente descrito pela análise das forças que atuam sobre ela
e aplicação da segunda lei de Newton:
G
G
Força peso: F peso = ρ silVg
G
G
Força de empuxo (do ar): Femp = −ρ arVg
G
G
Força de viscosidade: Fvisc = −6πRηv (lei de Stokes para um corpo esférico)
G
G
Força elétrica: Fel = qE
Lista de símbolos e valores das constantes:
R = raio da gotícula, suposta esférica.
V = volume da gotícula, suposta esférica: V =
4π 3
R
3
4
ρsil = densidade do óleo de silicone: ρsil = 1,075 × 103 kg/m3
ρar = densidade do ar à temperatura ambiente: ρar = 1,293 kg/m3
η = coeficiente de viscosidade do ar à temperatura ambiente: η = 1,82 × 10-5 kg/m.s
G
g = aceleração da gravidade local: g = 9,79 m/s2
G
v = velocidade da gotícula (constante).
q = carga elétrica da gotícula.
U = tensão entre as placas do capacitor.
d = distância entre as placas do capacitor: d = (2,50 ± 0,01) mm
G
G
E = campo elétrico entre as placas do capacitor: E = U / d
2. Após a aplicação da força elétrica em um ou outro sentido, o movimento da gotícula torna-se
rapidamente uniforme (velocidade constante). Assim a aplicação da segunda lei de Newton implica
em que a soma das forças acima deve ser zero.
3. Observe que, nas condições da experiência, a força elétrica possui o mesmo sentido da força peso no
movimento de descida da gotícula e o sentido oposto ao da força peso no movimento de subida
(estamos sempre nos referindo ao sentido real do movimento das gotículas, não àquele observado no
microscópio).
4. Por outro lado, a força de viscosidade possui sempre sentido oposto ao movimento da gotícula e a
força de empuxo possui sempre sentido oposto ao da força peso.
5. A partir da aplicação da segunda lei de Newton ao equilíbrio das gotículas (em movimento
uniforme) e utilizando as expressões acima, obtemos então as seguintes equações para as magnitudes
G
G
das velocidades de subida ( v s ) e de descida ( v d ):
vd =
1  qU 4 3

+ πR g (ρ sil − ρ ar )

6πRη  d
3

(1)
vs =
1  qU 4 3

− πR g (ρ sil − ρ ar )

6πRη  d
3

(2)
6. A manipulação dessas equações permite a obtenção de expressões para a carga e o raio da gotícula:
q=
vd + v s
9
η3
πd
2
g (ρ sil − ρ ar ) U
R=
3
2
vd − v s
η
vd − vs
g (ρ sil − ρ ar )
(3)
(4)
5
7. Com essas expressões é possível determinar a carga e o raio de cada gotícula analisada na
experiência, a partir de parâmetros medidos diretamente em laboratório – tensão elétrica e
velocidades de subida e descida das gotículas (obtidas a partir das distâncias percorridas e dos
tempos gastos nesses percursos) – e de parâmetros fornecidos (aceleração da gravidade, densidades
do óleo de silicone e do ar, viscosidade do ar, distância entre as placas do capacitor).
QUESTÕES E CONCEITOS A SEREM PREVIAMENTE COMPREENDIDOS
1. Deduza as equações 1-4. Empregue sempre notação vetorial e desenhe os diagramas de corpo livre
para as gotículas em cada uma das duas situações envolvidas (subida ou descida).
2. Apresente claramente o conceito de “coeficiente de viscosidade” de um fluido e discuta os limites de
aplicação da lei de Stokes, no que diz respeito ao tamanho e formato do objeto que se move através
do fluido.
3. Escreva e resolva a equação diferencial que descreve o movimento de descida da gotícula na
ausência de campo elétrico a partir do instante em que ela é abandonada com velocidade inicial nula.
Mostre que a solução dessa equação é da forma v d (t ) = v d
lim
(1 − e − t / t0 ) e determine os parâmetros
vdlim (velocidade limite) e t0 (constante de tempo característica do movimento) em função dos
parâmetros envolvidos no problema (raio da gotícula, densidade do óleo de silicone, densidade do ar,
aceleração da gravidade e viscosidade do ar).
4. Tome um valor típico para o raio da gotícula em torno de 10-6 m e calcule os valores de vdlim e t0.
Baseado nesses valores, quanto tempo é necessário esperar para que a gotícula atinja velocidade
constante? Discuta então se é lícito considerar que a gotícula descreve um movimento uniforme
durante a tomada de medidas de tempo efetuadas na experiência.
PROCEDIMENTOS E CÁLCULOS A SEREM EFETUADOS NO RELATÓRIO
1. Apresente em uma tabela todos os valores medidos em laboratório para tempos de subida, tempos de
descida e distâncias percorridas por cada gotícula analisada. Inclua na tabela os valores de tensão
utilizada em cada caso assim como os valores calculados para vs e vd. Identifique cada gotícula com
um número ou outro código que achar conveniente.
2. Apresente em uma outra tabela os valores de carga e raio de cada gotícula analisada. Explique
claramente qual foi o método utilizado para a determinação desses valores a partir das equações 3 e
4; mencione (e em caso afirmativo descreva) se foi utilizado algum algoritmo computacional para a
realização desses cálculos.
3. Na experiência original de Millikan, foram analisadas mais de mil gotículas em um trabalho de
longa duração, o que permitiu a realização de um tratamento estatístico minucioso para verificação
6
da hipótese de quantização da carga e determinação da carga elementar. Um tratamento similar é
inviável nas condições desta experiência, dado o número relativamente baixo de gotículas
analisadas. Pode-se entretanto obter uma percepção da quantização da carga a partir da montagem de
um histograma, onde os valores das cargas elétrica das diversas gotículas são representados num
gráfico de barras com largura fixa e altura proporcional à freqüência com que o valor de carga
correspondente a cada barra foi encontrado. Assim, uma barra posicionada ao longo do eixo das
abscissas entre as coordenada q e q + ∆q possuirá altura proporcional ao número de vezes em que
uma carga dentro desse intervalo foi obtida na coleção de gotículas analisadas. Tome ∆q na faixa de
0,1 a 0,5 × 10-19 C e monte um histograma como descrito acima, representando todas as gotículas
analisadas. (Veja mais detalhes sobre histogramas na referência 8.)
4. Interprete o histograma à luz da hipótese de quantização da carga elétrica, verificando a formação de
grupos de cargas centrados em determinados valores discretos. Indique esses grupos no histograma,
utilizando (se necessário) o valor atualmente aceito para a carga elementar (1,60 × 10-19 C) como
orientação para discriminar os diversos grupos. (Esse artifício não foi obviamente empregado por
Millikan, mas o elevado número de gotículas analisadas lhe permitiu distinguir claramente os grupos
de cargas encontrados. Veja a referência 5.)
5. Determine o valor médio da carga de cada grupo, tomando as médias ponderadas das várias cargas
encontradas ou ajustando uma distribuição apropriada (gaussiana, por exemplo). Determine também
a incerteza nesse valor médio, através de um cálculo de desvio padrão ou da semi-largura da curva
ajustada.
6. Monte um gráfico dos valores médios de carga (qn) – com incerteza – encontrados para cada grupo
em função de um índice inteiro (n) que identifique cada grupo e que cresça de uma unidade de um
grupo para o próximo (por exemplo: n = 1 para o primeiro grupo, n = 2 para o segundo, etc). Calcule
o coeficiente angular desse gráfico (com incerteza) e compare com o valor aceito para a carga
elementar.
7. Monte um gráfico da carga de cada gotícula em função de seu raio e verifique se há alguma
correlação visível entre essas duas grandezas. Indique nesse gráfico (com linhas horizontais) os
valores de cargas médios obtidos para cada grupo de cargas com diferentes valores de n.
DISCUSSÕES ADICIONAIS
1. Assumindo como verdadeira a hipótese de quantização da carga elétrica, não podem ser de modo
algum encontrados valores de cargas elétricas para as gotículas diferentes de múltiplos inteiros de e.
Na sua opinião, os resultados obtidos nesta prática são conclusivos para a verificação dessa
hipótese? Considerando que a quantização da carga elétrica é hoje universalmente aceita, qual seria a
7
razão para a ocorrência de valores de carga para as gotículas fora da condição de quantização? Onde
estão as principais fontes de erro experimentais?
2. A lei de Stokes deixa de ser rigorosamente válida para gotículas com raios muito pequenos,
comparáveis ao livre caminho médio das moléculas de ar. Explique qual a razão física para a não
aplicabilidade da lei de Stokes em tal situação.
3. Nesse caso, Millikan mostrou que pode-se empregar uma correção à lei de Stokes substituindo o
coeficiente de viscosidade constante η por uma valor efetivo dependente do raio R da gotícula
através da expressão η ef =
η
, sendo p a pressão atmosférica dentro da câmara e b uma
1 + b / pR
constante positiva. Mostre que ηef se reduz a η para gotículas de raios grandes e/ou a pressões
elevadas e discuta esse fato.
4. Como a correção à lei de Stokes descrita acima afeta os valores obtidos para as cargas das gotículas?
O que deveria ser modificado nos procedimentos empregados para levar em conta essa correção?
5. Discuta a importância histórica da experiência de Millikan.
6. Há alguma correlação óbvia entre os valores de cargas e raios obtidos para as diversas gotículas
analisadas? Se a carga de cada gotícula é quantizada, seu raio também é?
7. Além da carga elétrica, dê exemplos de outras grandezas que apresentam caráter quantizado e
comente sobre evidências experimentais dessa quantização.
BIBLIOGRAFIA
1. D. Halliday, R. Resnick, J. Walker, Fundamentos de Física, Vols. 1, 2 e 3, LTC, 4a ed., Rio de
Janeiro, 1993.
2. Laboratory Experiments in Physics, 5.1.01, Phywe Systeme GmbH, Göttingen, 1999.
3. J. Goldemberg, Física Geral e Experimental, 3o Vol, Ed. da Universidade de São Paulo, São Paulo,
1973.
4. A. C. Melisinos, Experiments in Modern Physics, Academic Press, New York, 1966.
5. R. A. Millikan, “On the elementary electrical charge and the Avogadro constant”, Physical Review,
Vol. 2, pp. 109-143, 1913.
6. H. Fletcher, “My work with Millikan on the oil-drop experiment”, Physics Today, June 1982, pp.
43-47.
7. M. Alonso, E. J. Finn, Física: um curso universitário, Ed. Edgar Blücher, São Paulo, 1972.
8. J. H. Vuolo, Fundamentos da Teoria dos Erros, Ed. Edgar Blücher, 2a ed., São Paulo, 1996.
Redação: Prof. Jair C. C. Freitas
Colaboração: Monitores Danilo Oliveira de Souza e Alan Gomes Bossois.
8
Grupo ___: ___________________; ___________________;__________________
Data: ____________
FOLHA DE DADOS
Processo de calibração:
Divisões na escala de observação (tela):
_______ _______ _______ _______
Divisões correspondentes na escala
de calibração (lâmina):
_______ _______ _______ _______
Movimento das gotículas:
Gota:
_____
d (__):
ts
(__)
td
(__)
Gota:
_____
d (__):
ts
(__)
td
(__)
Gota:
_____
d (__):
_____
_____
_____
U (__)
U (__)
U (__)
______
______
______
Gota:
_____
d (__):
ts
(__)
td
(__)
Gota:
_____
d (__):
ts
(__)
td
(__)
Gota:
_____
d (__):
_____
_____
_____
U (__)
U (__)
U (__)
______
______
______
Gota:
_____
d (__):
ts
(__)
td
(__)
Gota:
_____
d (__):
ts
(__)
td
(__)
Gota:
_____
d (__):
_____
_____
_____
U (__)
U (__)
U (__)
______
______
______
ts
(__)
td
(__)
ts
(__)
td
(__)
ts
(__)
td
(__)
9