Experimento de Millikan - Stoa

Experimento de Millikan
Grupo 312 - Leandro Donizeti Ribeiro, Marcio Koji Umezaw, Henrique Romeo
Instituto de Física – Universidade de São Paulo
Disciplina FNC 0313 – Prof. Dra. Elisabeth Mateus Yoshimura
27 de setembro de 2007
Resumo
Este experimento consistiu em determinar a quantização da carga elétrica e o valor da carga elementar, assim
como estudar os métodos experimentais utilizados, com intuito de obter uma incerteza relativa o menor
possível. Isto foi feito utilizando um método semelhante ao utilizado por Millikan, ou seja, medindo as
velocidades de subida e descida de gotas de óleo, sob a ação de um campo elétrico, porém neste experimento
foram utilizados equipamentos computacionais a fim de otimizar o processo de medida. Usando tanto os
dados do grupo (62 gotículas analisadas) como com os dados de toda a classe (um total de 249 gotículas),
procurou-se observar tanto a quantização da carga elétrica quanto a determinação de seu valor, obtendo
resultados bastante satisfatórios.
Introdução
A realização deste experimento é
conceitualmente
simples,
no
entanto,
os
experimentos efetuados por Millikan e Flechter
provocaram um grande impacto sobre os conceitos
que até então vigoravam em física atômica,
rendendo assim o prêmio Nobel a Millikan em
1923.
A importância do experimento de Millikan
consiste no fato de este observar a quantização da
carga elétrica elementar, além é claro de fornecer o
valor de tal carga, uma das constantes fundamentais
da natureza. O experimento realizado no
Laboratório Didático é essencialmente o mesmo
daquele realizado por Millikan e Flecther em 1910,
do qual há um pequeno resumo a seguir.
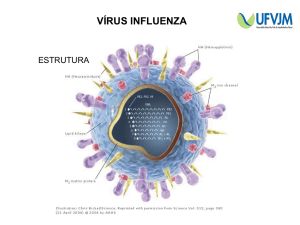
Figura 1 - Equipamento utilizado por Fletcher para
determinação da carga elétrica elementar.
O arranjo experimental é esquematizado na
figura 1. O atomizador de perfume foi usado para
borrifar óleo de relógio na câmara acima do
capacitor. Durante a pulverização algumas gotículas
de óleo ionizam-se por atrito. Quando essas
gotículas penetram no capacitor, ficam sob a ação
do campo elétrico que há entre as placas do
capacitor.
Nos primeiros experimentos, Fletcher
investigou o efeito de um campo criado pela
aplicação de um potencial de 1000 volts.
Imediatamente observou (através do pequeno
telescópio) que algumas gotículas subiam
lentamente, enquanto outras desciam rapidamente,
um resultado lógico para quem sabia que algumas
1
gotículas estavam positivamente carregadas, e
outras negativamente. Ligando e desligando a
bateria na freqüência adequada, ele conseguia
selecionar uma gotícula e mantê-la no seu campo de
visão por um longo tempo. Com algumas medidas e
o tratamento matemático utilizado por Millikan e
Begeman, Fletcher obteve, com seu rústico
equipamento, resultados bastante razoáveis. Logo
depois Millikan encomendou uma montagem
"profissional", com a qual obteve um valor mais
preciso para a carga elementar de 4,774(5) statC. O
valor aceito atualmente é de 4,803×10-10 statC.
Como as dimensões das placas do capacitor
são muito maiores que a distância entre elas, podese desprezar os efeitos de borda, considerando o
campo elétrico constante, dado por E = V / d, onde
V é diferença de potencial entre as placas e d a
distância entre as placas do capacitor.
As gotículas em questão estavam sujeitas às
forças elétrica:


Fel  qE ;
Descida:
gravitacional:
Subida:
Quando as gotículas de óleo atingem a
velocidade terminal, as forças resultantes nas
gotículas, quando estas estão subindo ou descendo,
são nulas e dadas por:
4. 3
a .g.( óleo  ar )  qE  6. . .a.v d  0
3
[1]
4. 3
a .g.( óleo  ar )  qE  6. . .a.v s  0
3
[2]


P  mg ;
o empuxo, que no caso dessas gotículas é dado por:

  
Fempux  m. ar .g
  óleo  ;
Somando as equações acima, temos que o
raio da gotícula é obtido pela relação:
a2 
e a força viscosa, dada pela Lei de Stokes:


Fv  6. ..a.v ,
9..(vd  v s )
4.g (  óleo   ar )
[3]
E subtraindo-as, temos que a carga da gotícula é
obtida pela relação:
onde q é a carga da gotícula, E é o campo elétrico
aplicado, m é a massa da gotícula, g é a aceleração
da gravidade, ρar e ρóleo são respectivamente as
densidades do ar e do óleo, η é o coeficiente de
viscosidade do ar, a é o raio da gotícula e v a sua
velocidade.
q
3. ..a.(vd  vs ).d
V
[4]
Millikan e Flechter também estudaram com
cuidado a Lei de Stokes, e verificaram que a
viscosidade do ar, determinada para o caso de
objetos macroscópicos, deveria sofrer uma pequena
correção devido ao pequeno tamanho das gotículas.
O tamanho destas são comparáveis com o livre
caminho médio das moléculas de ar, e portanto o ar
não se comporta como um “fluído contínuo”, como
é o caso para as esferas de raios muito maiores. A
lei de Stokes correta é obtida calculando-se a
viscosidade do ar para uma gotícula pequena com:
Assim, uma gotícula com a força elétrica
para baixo, paralela à gravidade, faz com que a
gotícula seja acelerada para baixo, aumentando sua
velocidade e com isso também a força resistiva, até
que esta se iguale à soma das outras forças de
sentido contrário, fazendo com que a gotícula atinja
uma velocidade constante (velocidade terminal).
Como o tempo gasto na parte acelerada do
movimento é muito curto (da ordem de 10-6 s), a
gotícula é sempre observada em movimento
uniforme. Invertendo-se o campo elétrico
(escolhendo E de tal forma que qE > mg) esta
mesma gotícula passa a fazer um movimento
ascendente.

0
1
2
b
p.a
[5]
onde η0 é o coeficiente de viscosidade à temperatura
ambiente e b = 6,17x10-4 cmHg é uma constante
determinada pelo próprio Millikan para se levar em
consideração o fato de que as dimensões da gotícula
são comparáveis às distâncias inter-moleculares do
ar atmosférico.
possuía pequenos furos na parte superior para a
entrada das gotículas. Ele também estava ligado a
uma fonte de tensão contínua com uma chave
inversora por onde era possível mudar o sentido da
corrente e conseqüentemente o campo elétrico no
capacitor. A tensão da fonte era medida com o uso
de um multímetro digital.
Temos finalmente para o raio da gotícula:
b
a

2. p
Antes de se tomar as medidas foi feita a
limpeza do capacitor para retirar resíduos de óleo
que poderiam influenciar no movimento das
gotículas dentro do campo elétrico, além de se
verificar o nivelamento das placas do capacitor,
ajustes do foco e do ângulo de iluminação, bem
como a medida da distância d entre as placas.
2
9. 0 .(v d  v s )
 b 

 
4.g (  óleo   ar )
 2. p 
[6]
Arranjo experimental
As medidas eram feitas borrifando-se o óleo
através dos orifícios na parte superior do capacitor.
Quando havia bastante gotículas no campo de visão
do vídeo, o campo elétrico era então ligado e seu
sentido era alterado em uma certa freqüência afim
de que se pudesse medir sucessivas subidas e
descidas de uma dada gotícula. Esse movimento foi
registrado em vídeo repetidas vezes para serem
analisados posteriormente através do software
VideoPoint. Foram feitos dois conjuntos de medidas
com óleos diferentes, quinze vídeos para cada um
dos dois tipos de óleo.
Após as medidas o capacitor foi retirado e
no seu lugar foi colocada uma escala calibrada cuja
imagem foi capturada para referência na análise das
gotículas, pois o VídeoPoint nos dá medidas em
pixels e através da imagem da escala pode-se obter
o fator de conversão em cm/pixel.
Figura 2 - Aparato para obtenção das velocidades das
gotículas de óleo dentro do campo elétrico.
Descrição das Medidas
O VídeoPoint é um software utilizado para
se medir a evolução de um dado objeto no tempo,
marcando sua posição em um vídeo quadro a
quadro. Escolhendo-se gotículas que apareciam no
vídeo em movimentos de subida e descida por
tempo suficiente, se obtém um gráfico de posição
com relação ao tempo como mostrado na figura 3:
O aparato experimental é mostrado na figura
2. No alto do suporte (à esquerda na figura)
encontra-se um microscópio na horizontal, onde na
ocular foi acoplada uma câmera digital ligada a um
computador para aquisição de dados. Do outro lado
uma fonte de luz com ângulo ajustável serviu para
iluminação das gotículas de óleo que eram
borrifadas com um nebulizador dentro de um
capacitor de placas paralelas. O capacitor estava
isolado nas laterais para evitar a influência de
correntes de ar no movimento das gotículas, mas
3
Ainda na equação 6, separamos os termos
que a constituem para analisar o efeito das
incertezas no valor final. Definimos esses termos
como segue:
500
450
400
A
Posição (pixel)
350
300
b
; B  9. 0 .(vd  v s ); C  4.g. óleo
2. p
O efeito da incerteza de cada termo,
representado pela incerteza relativa, é apresentado
na tabela 1:
250
200
150

medida
A
0,07%
B
~ 10,0%
C
0,24%
Tabela 1 – incerteza relativa dos termos da equação 6.
100
50
0
10
20
30
40
50
Tempo (s)
A incerteza relativa do termo B é variável
por causa da incerteza das velocidades, que depende
da quantidade de termos na média, mas em todas as
gotículas ficou em torno de 10%.
Figura 3 - Gráfico de posição por tempo de uma gotícula
de óleo dentro de um campo magnético de direção e
módulo constantes e sentido variável.
A incerteza da posição da gotícula foi
considerada como o diâmetro do cursor do
VideoPoint, medido em 0,05 mm. Podemos aqui
desconsiderar o efeito browniano, observável nos
vídeos, porém muito menor que a incerteza
utilizada.
Por sua vez, contribuem para a incerteza do
termo B as incertezas da diferença das velocidades
de subida e descida e do coeficiente de viscosidade
do ar 0. Comparando as incertezas relativas dessas
duas, vemos que a primeira é cerca de 200 vezes
maior que a segunda. Portanto, no cálculo de
propagação da incerteza do raio da gota, apenas
levou-se em consideração o termo referente à
incerteza das velocidades, que é maior que as outras
de um fator de aproximadamente 2x103.
Com o software Origin, foram medidas as
velocidades de subida e descida das diversas
gotículas como sendo o coeficiente angular das retas
mostradas na figura 3, se obtendo também suas
incertezas. Essas incertezas foram combinadas com
o desvio padrão da média, pois para se obter os
valores finais de velocidades de subida e descida se
faziam médias simples entre os valores obtidos no
gráfico.
Para a equação 4, que dá o valor da carga
elétrica da gota, temos as incertezas relativas
apresentadas na tabela 2:
medida
0,57%
a
4,48%
d
0,44%
V
1,00%
Tabela 2 – incerteza relativa dos termos da equação 4.

Antes de apresentar os resultados para os
raios das gotículas e suas cargas elétricas, é feita
uma análise sobre os termos da equação 6 e as
incertezas das equações 4 e 6.
Na equação 6, que dá o valor do raio da
gota, vemos que há uma soma entre as densidades
do óleo e do ar. A densidade do ar é
aproximadamente 800 vezes menor que a densidade
do óleo, e como a sua determinação é trabalhosa e
não mudaria o valor final dentro dos dígitos
significativos, optou-se por desprezá-la.
Para a propagação da incerteza da carga q,
vê-se que não se podem desprezar nenhum termo,
até porque não seria tão necessário, pois este cálculo
é relativamente simples.
4
as do primeiro (calculando-se a média se vê isto
claramente), mas o raio das gotas não variou. A
vantagem disso é que se têm mais gotículas com
cargas pequenas, próximas à carga fundamental,
porém havia mais gotículas sem carga no segundo
que no primeiro, o que dificultava a tomada dos
dados, por esse motivo a segunda tabela tem menos
valores que a primeira, apesar de terem sido feitos
quantidades iguais de vídeos para os dois.
Resultados
São apresentados nas tabelas 3 e 4 os valores
de raio e carga das gotículas analisadas, a primeira
para as medidas utilizando-se o óleo do primeiro
tipo e a segunda utilizando-se o óleo do segundo
tipo.
a ±  (cm)
q ±  (statcoulomb)
6,04E-05
2,70E-06
1,71E-09
7,95E-11
6,70E-05
2,37E-05
2,03E-09
7,22E-10
5,40E-05
4,07E-06
2,00E-09
1,54E-10
6,93E-05
2,54E-06
2,80E-09
1,08E-10
6,99E-05
2,99E-06
6,57E-09
2,92E-10
7,49E-05
3,70E-06
5,48E-09
2,79E-10
6,81E-05
1,86E-06
3,18E-09
9,44E-11
6,31E-05
1,83E-06
3,37E-09
1,05E-10
6,61E-05
2,24E-06
2,79E-09
9,99E-11
7,21E-05
1,77E-06
4,16E-09
1,12E-10
7,61E-05
4,48E-06
5,81E-09
3,50E-10
6,76E-05
2,86E-06
2,64E-09
1,16E-10
6,29E-05
2,70E-06
2,71E-09
1,21E-10
6,57E-05
2,92E-06
3,84E-09
1,77E-10
5,43E-05
3,24E-06
1,81E-09
1,10E-10
6,35E-05
3,53E-06
2,14E-09
1,22E-10
7,25E-05
2,63E-06
3,73E-09
1,42E-10
8,18E-05
5,48E-06
6,69E-09
4,56E-10
7,22E-05
4,06E-06
5,35E-09
3,08E-10
Tabela 3 – Raios e cargas das gotículas de óleo do primeiro
tipo analisadas.
Análise dos Dados
A seguir é apresentado o histograma de
todas as cargas obtidas.
Frequencia
4
2
0
0
1
2
3
4
5
6
7
8
-9
Carga (10 statC)
a ±  (cm)
q ±  (statcoulomb)
6,63E-05
2,43E-06
9,71E-10
3,60E-11
7,27E-05
2,89E-06
1,03E-09
4,13E-11
7,72E-05
4,59E-06
1,08E-09
6,45E-11
5,96E-05
3,61E-06
5,87E-10
3,59E-11
7,20E-05
2,35E-06
1,07E-09
3,52E-11
5,29E-05
1,40E-06
4,78E-10
1,29E-11
6,58E-05
1,61E-06
4,80E-10
1,20E-11
5,60E-05
3,74E-06
5,66E-10
3,81E-11
5,67E-05
4,86E-06
1,02E-09
8,82E-11
5,99E-05
2,26E-06
6,14E-10
2,35E-11
7,62E-05
2,20E-06
1,15E-09
3,35E-11
6,69E-05
1,61E-06
5,36E-10
1,31E-11
6,66E-05
3,06E-06
1,00E-09
4,65E-11
Tabela 4 – Raios e cargas das gotículas de óleo do segundo
tipo analisadas.
Figura 4 - Histograma de cargas elétricas das gotículas.
No histograma podem-se identificar cinco
agrupamentos de valores nos intervalos: 0,4 a 0,7;
0,9 a 1,2; 1,6 a 1,9; 2,0 a 2,4; 2,5 a 2,8. Supondo
que a carga elétrica é quantizada o conclui-se que o
valor médio < q > de cada um dos 5 agrupamentos
se refere a múltiplo inteiro do valor da carga.
Nesses intervalos calculamos o valor médio < q > e
obtemos os valores apresentados na tabela 5:
Não foi informada a diferença entre os dois
óleos, mas notamos que as cargas das gotículas do
segundo tipo de óleo eram, em geral, menores que
5
Intervalo
< q > ± (statC)
1
5,44E-10 2,29E-11
2
1,05E-09 2,25E-11
3
1,77E-09 3,86E-11
4
2,17E-09 4,74E-11
5
2,68E-09 3,55E-11
14
13
12
11
10
Frequência
9
Tabela 5 – Valores de cargas calculadas a partir do
histograma da figura 4.
8
7
6
5
4
3
2
1
Com esses valores, se traçou o gráfico:
0
0,0
0,4
0,8
1,2
1,6
2,0
2,4
2,8
3,2
3,6
4,0
4,4
4,8
-9
Carga (10 statC)
3,0
Figura 6 - Histograma de cargas das gotas da classe.
2,0
Neste histograma é claramente visível
apenas o primeiro agrupamento de valores, e depois
dele se podem ver, com dificuldade, mais dois
agrupamentos, nos intervalos: 0,24 a 0,72; 0,72 a
1,28; 1,28 a 1,6. Procedeu-se da mesma forma que
no caso anterior, obtendo-se a reta da figura 7:
-9
Carga (10 statC)
2,5
1,5
1,0
0,5
1
2
3
4
5
1,6
n
1,4
Carga (10 statC)
Figura 5 - Reta de carga em função do índice do intervalo.
-9
Este gráfico representa claramente uma reta,
cuja equação é:
 q   n.e  b , onde n é um múltiplo
1,2
1,0
0,8
0,6
inteiro, e é a carga fundamental procurada e o
coeficiente linear b é esperado zero. Do gráfico da
figura 5 obtemos os seguintes valores:
0,4
1
2
3
n
b ±  (statC)
e ±  (statC)
-2,47E-12
5,44E-10
6,21E-11
2,28E-11
Figura 7 - Reta de carga em função do índice do intervalo.
O gráfico da figura 7 apresenta os seguintes
coeficientes angular e linear:
Vê-se que o coeficiente linear é compatível
com zero e que a carga elétrica fundamental foi
calculada como 5,44(23)x10-10 statC.
b ±  (statC)
e ±  (statC)
Com os dados dos outros grupos da sala,
construímos um novo histograma, apresentado na
figura 6:
6
1,06E-10 6,69E-11
4,53E-10 3,12E-11
Novamente, o coeficiente linear b é
compatível com zero dentro de duas incertezas e o
coeficiente angular nos dá a carga elementar e com
o valor de 4,53(31)x10-10 statC.
carga mais nitidamente, porém não foi isso o que
ocorreu, ou seja, a verificação da quantização foi
mais difícil, pois os dados estavam distribuídos com
uma uniformidade maior, exceto um agrupamento
em torno do valor de uma carga elementar. Mesmo
assim, foi possível calcular um valor de carga
elementar para este conjunto de dados, obtendo-se o
valor de 4,53(31)x10-10 statC. Vê-se que este valor é
compatível, dentro de uma incerteza, com o valor
atualmente aceito, porém sua incerteza relativa é de
6,9%, maior que a obtida por este grupo.
Conclusão
Para a determinação da carga elétrica
elementar, repetiu-se o experimento de Millikan
com o uso de equipamentos computacionais afim de
se reduzir incertezas e facilitar o processo de
tomada de dados. O experimento consistia
basicamente na medição de velocidades de subida e
descida de gotículas de óleo eletricamente
carregadas, sob a ação de um campo elétrico entre
as placas de um capacitor através de um software de
análise de vídeos.
Analisando estes dados, nota-se que a
uniformização das medidas dos diferentes grupos
pode melhorar os resultados finais do experimento,
criando-se regras para as medidas das velocidades
das gotículas e análise geral dos dados, regras essas
que podem ser discutidas entre os grupos durante a
tomada de dados.
A análise deste experimento consistiu em
duas partes. A primeira delas foi o de analisar as
gotas deste grupo. Foi possível verificar a
quantização da carga elétrica, uma vez que no
histograma dos valores de cargas das gotículas
analisadas, haviam picos os quais acredita-se serem
referentes a um dado valor múltiplo da carga
elementar. Foi utilizado também dois diferentes
tipos de óleo e verificou-se que a vantagem de se
usar o segundo tipo é que ele apresenta gotículas
com cargas menores que o primeiro, melhorando a
observação da quantização e determinação do valor
da carga elementar.
Referências
H. Fletcher, My work with Millikan on the oil-drop
experiment. Physics Today, June 1982, p.43.
Apostila da disciplina de Física Experimental V
(Estrutura da matéria) – FNC-313 – Millikan, IFUSP,
2007.
R. A Millikan, the isolation of an ion, a precison
measurement of its charge, and the correction of Stoke’s
Law. Science, 30 September 1910.
Com os dados do grupo foi possível calcular
o valor da carga elementar, obtendo o valor de
5,44(23)x10-10 statC, valor este próximo do valor
atualmente aceito de 4,803×10-10 statC dentro de
três incertezas. A incerteza obtida é da ordem de
4,2%, ou seja, a precisão do valor obtido é boa, mas
poderia ser melhorada com um maior cuidado na
medida das velocidades, já que é este o fator
principal que contribui para as incertezas neste
experimento.
V. Ribas-Estrutura da matéria (Notas de aula).
http://www.dfn.if.usp.br/~ribas/download.html
Microcal Origin – Gráficos e ajustes de pontos
experimentais - http:/ /www.microcal.com
J. H. Vuolo, Fundamentos à teoria de erros, 2º edição –
Editora Edgard Blücher.
Página Web da disciplina:
http://www.labdid.if.usp.br/~estrutura
A segunda parte deste experimento consistiu
em analisar os dados dos grupos da classe. O
procedimento de análise foi o mesmo que o
utilizado para os dados deste grupo. Era esperado
que, com um número maior de dados, se obtivesse
um histograma que apresentasse a quantização da
http://nobelprize.org/nobel_prizes/physics/laureates/192
3/
7